今回はまた用語の勉強に戻ります。 波の分野を勉強しているわけですが,すでにいろいろな用語が出てきました。 振幅,波長,振動数などなど。。。
しかし,これらの用語は覚えるのはさほど苦にならなかったと思います。 なぜなら,振幅→媒質の振れ幅,波長→波1個分の長さ,振動数→1秒間の振動の回数,といった具合に,漢字そのままの意味だから笑
今回は漢字からはちょっと意味が想像できない用語,「位相」について学びましょう。
波の位相とは何か
「媒質の振動の状態を表す量を位相という。」と教科書には書いてあるのですが,いまいちピンときませんよね?
この位相という用語は,漢字からも意味が想像できないし,説明を聞いてもあまりよくわからないという困ったちゃんなのです笑
そこで,ここでは具体例を与えて説明に替えたいと思います。 具体例というのは「同位相」と「逆位相」です。
位相というのは,媒質の異なる2点の振動状態を比較するのに使われます。「この点とあの点の位相は◯◯ずれている」というような感じ。
その中でもわかりやすいのが,「位相がずれていない(=同位相)」と「位相が真逆(=逆位相)」のパターン。
最初に学習する段階ではこれだけ知っておけばとりあえずOK! これは言葉で説明するよりまとめノートを見てもらったほうが早いので,いきなりですがまとめておきましょう。
今回のまとめノート
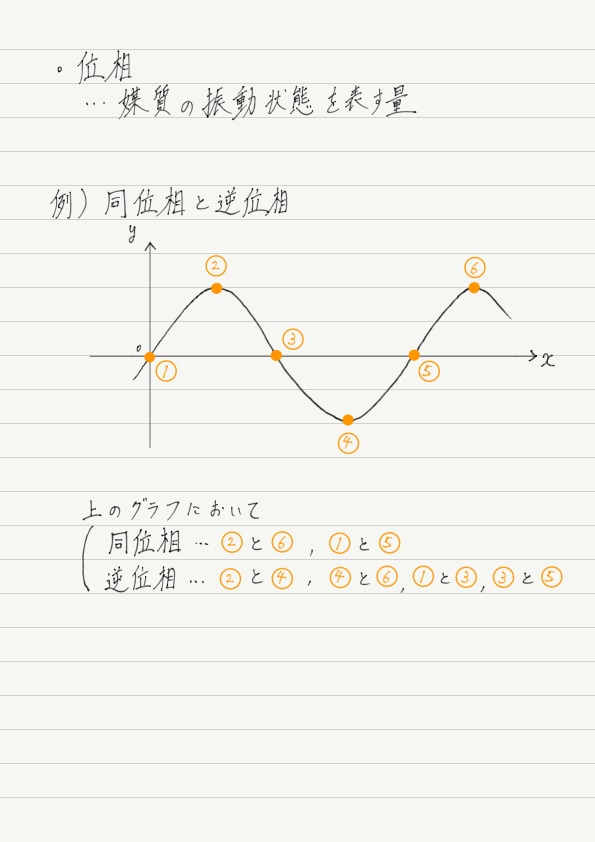
まとめノートのとおり,図の②と⑥は同位相です。 具体的に何が同じなのかというと,「どちらも波の山」ということ。 振動の状態が同じというのはこういう意味なのです。
同じ要領で,谷と谷も同位相になります。
一方,②と④(あるいは④と⑥)の場合,山と谷は正反対なので,逆位相です。 なんとなく分かってきたんじゃないでしょうか?
(正確に説明していないので,現段階ではなんとなくの理解で結構です)
ただしこれだけだと,「変位(y座標の値)で区別しているんだな!」と勘違いしてしまう人が出てきそうなので,山と谷以外の場所での位相も考えてみます。
たとえばx軸との交点である,①,③,⑤の関係はどうでしょうか?
これらの点の変位はすべてy=0で同じです。 しかし,位相はすべて同じではありません。
同じx軸との交点でも,グラフが右上がりのときに交わる(①,⑤)のか,右下がりのときに交わる(③)のかで区別します。
よって,①と⑤は同位相で,①と③(または③と⑤)は逆位相になります。
さて,位相は振動状態を表す “量” なので,本来は数値です。
ですが,それはもっと学習が進んで,準備ができてから別の機会にあらためて説明することにします。
今回の内容に関する演習問題を用意したので,時間に余裕がある人は,ぜひチャレンジしてみてください!
次回予告
次回は波の分類について学びます!!