物理【電磁気】第37講『RLC直列回路』の講義内容に関連する演習問題です。
講義編を未読の方は問題を解く前にご一読ください。
問題
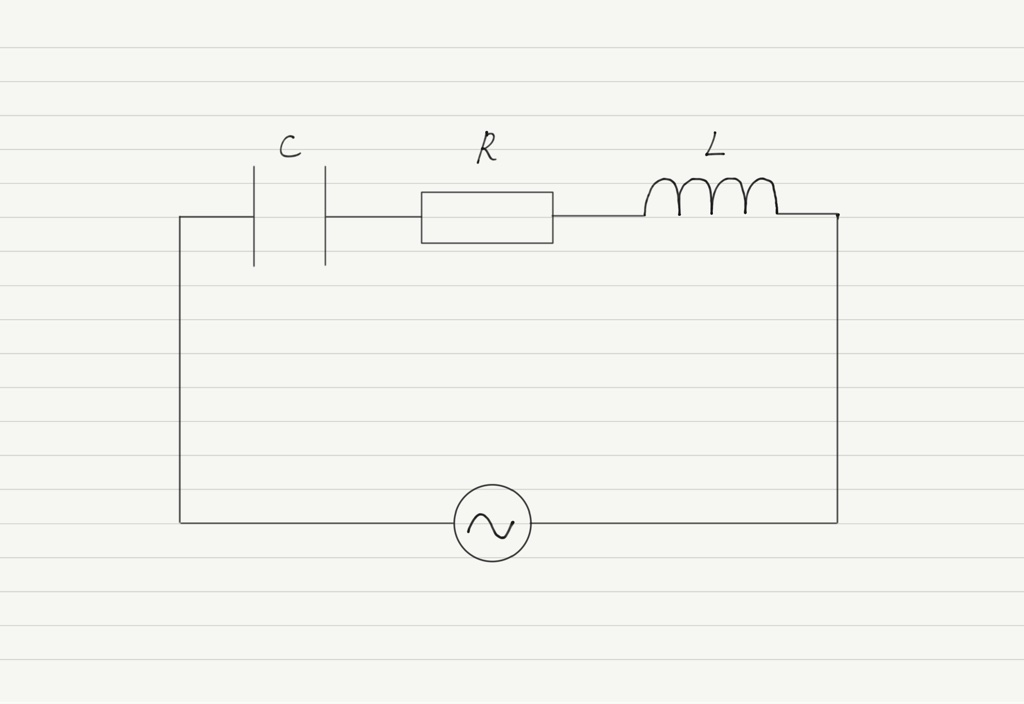
電気容量C[F]のコンデンサー,R[Ω]の抵抗,自己インダクタンスL[H]のコイルからなる下図のような直列回路に,角周波数ω[rad/s]の交流電圧Vを加える。
以下の各問に答えよ。
[Level.1]
回路に流れる電流Iの位相を基準(I=I0sinωt)とする。
電流Iの位相に対する,加えた電圧Vの位相のずれφについて,tanφの値を求めよ。
[Level.2]
この回路のインピーダンスZを求めよ。
[Level.3]
Zが最小となるときの周波数を求めよ。
この下に答えを載せていますが,まずは自力で考えてみましょう。
答え
[Level.1]
\(\tan \phi =\frac{\omega L-\frac{1}{\omega C}}{R}\)
[Level.2]
\(Z=\sqrt{R^{2}+(\omega L-\frac{1}{\omega C})^2}\)
[Level.3]
\(\displaystyle \frac{1}{2\pi \sqrt{LC}}\)