物理【波】第1講『正弦波の式』の講義内容に関連する演習問題です。
講義編を未読の方は問題を解く前にご一読ください。
問題
[Level.1]
x軸上を正の向きに進む正弦波がある。 位置xにおける媒質の変位yが,時刻tにおいて
\(y=-1.2\sin \pi (4.0t-\frac{x}{0.80})\)
と表されるとき,この正弦波の振幅,波長,周期,振動数,速さをそれぞれ求めよ。
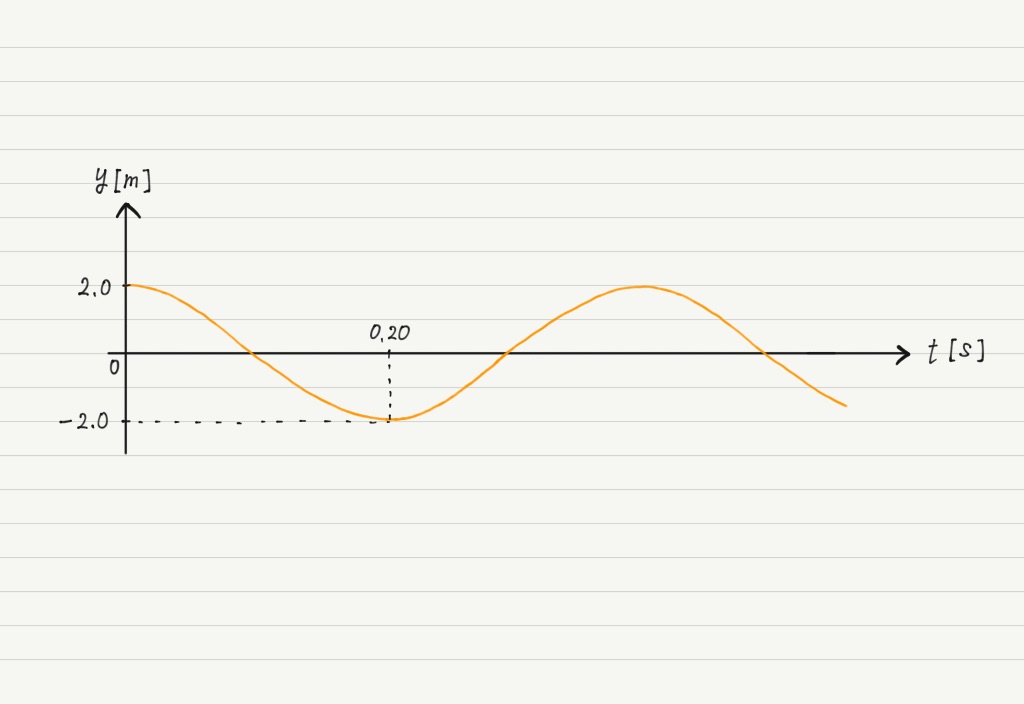
[Level.2]
x軸上を正の向きに0.50m/sで進む正弦波がある。
下図のy-tグラフは原点での媒質の変位を表している。
時刻tでの位置xにおける媒質の変位yを表す式を書け。
[Level.3]
正弦波の式を用いて,位相がπずれたとき(逆位相)の変位が,元の変位の符号だけ変わったものになることを証明せよ。
この下に答えを載せていますが,まずは自力で考えてみましょう。
答え
[Level.1]
振幅:1.2m
波長:1.6m
周期:0.50s
振動数:2.0Hz
速さ:3.2m/s
[Level.2]
\(y=2.0\cos 5\pi (t-2x)\)
[Level.3]
位相部分にπを足し,加法定理を用いる。