X線の正体は電磁波なので波の性質をもっているはずです。
今回はX線の波動性が顕著に現れる現象について詳しく見ていきましょう。
X線の回折・干渉
波特有の現象はいくつかありますが,その中でも特に重要なものとして「ヤングの実験」が挙げられます。
スリットを抜けた光が回折&干渉をした結果,縞模様が現れるという実験でした。
X線でも同様の現象が起こることが知られていますが,ヤングに実験の光源をX線に変えただけでは残念ながらうまくいきません。
ヤングの実験のスリット幅がX線の波長に比べて大きすぎるからです。
回折格子でもまだ大きすぎます(スリット幅が波長より大きいと回折は起こらない)。
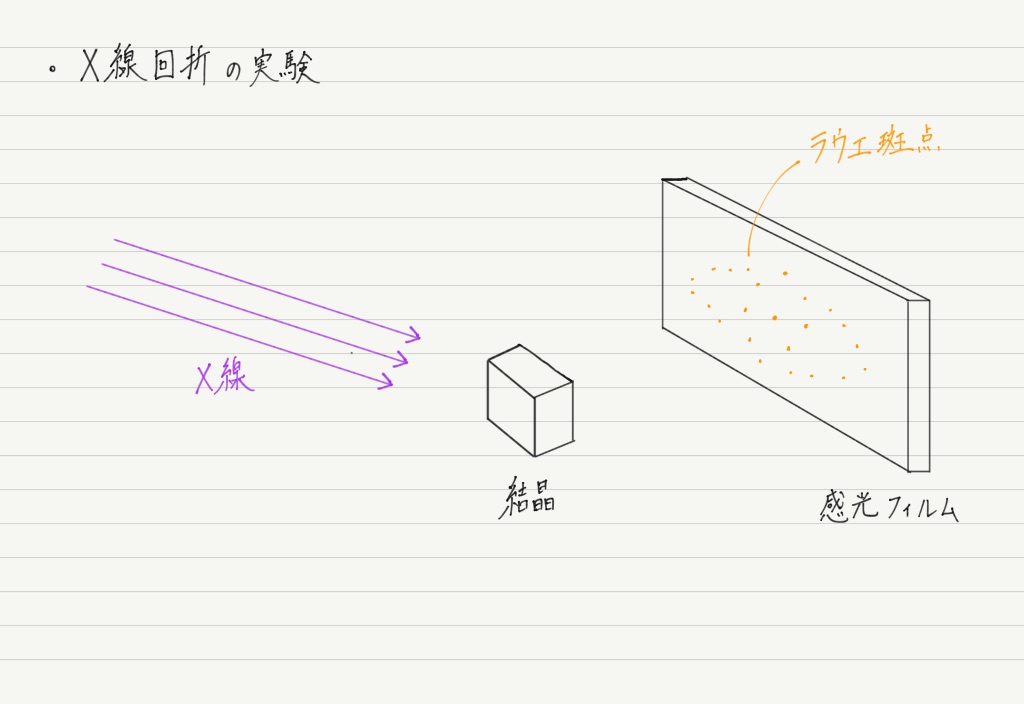
そんなわけで普通の光と同じ実験ではダメなのですが,回折格子の代わりに食塩などの結晶を用いるとうまく回折が起こり(結晶内の原子の間隔がX線の波長と同程度のため),干渉模様が見えることが知られています!
ただし,干渉模様はヤングの実験や回折格子と異なり,多数の点がポツポツと分布しているような模様(ラウエ斑点と呼ぶ)になります。
模様こそちがいますが干渉である以上,ラウエ斑点はX線どうしが強めあってできているはずです。
何をやるかはわかってますね?
そうです! 強めあう条件を探りましょう!!
X線が強めあう条件
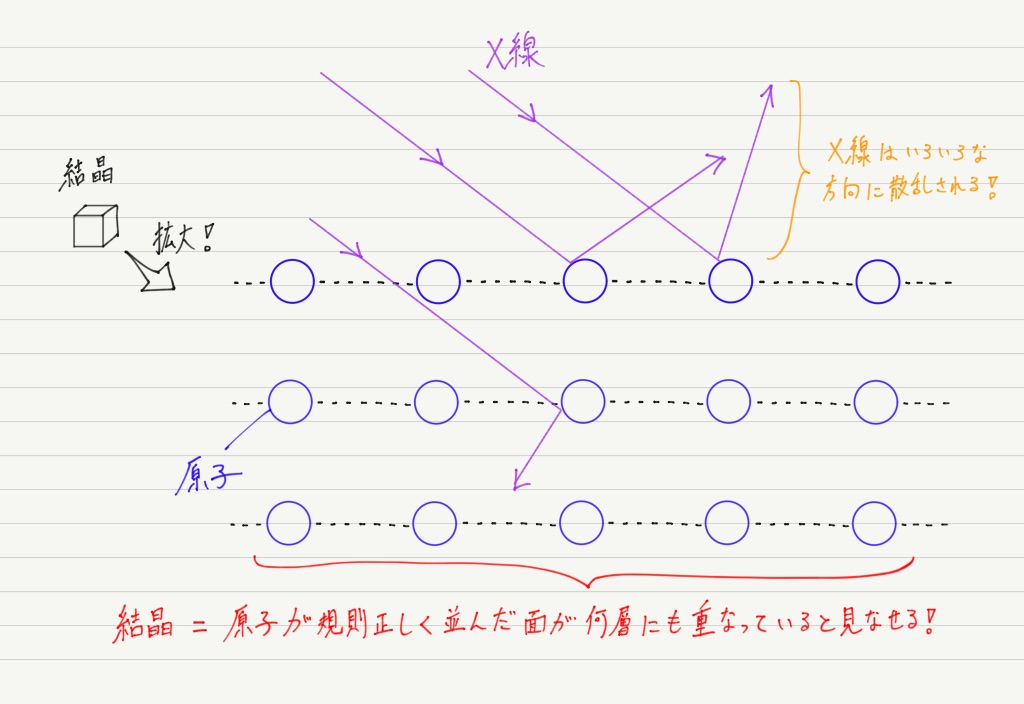
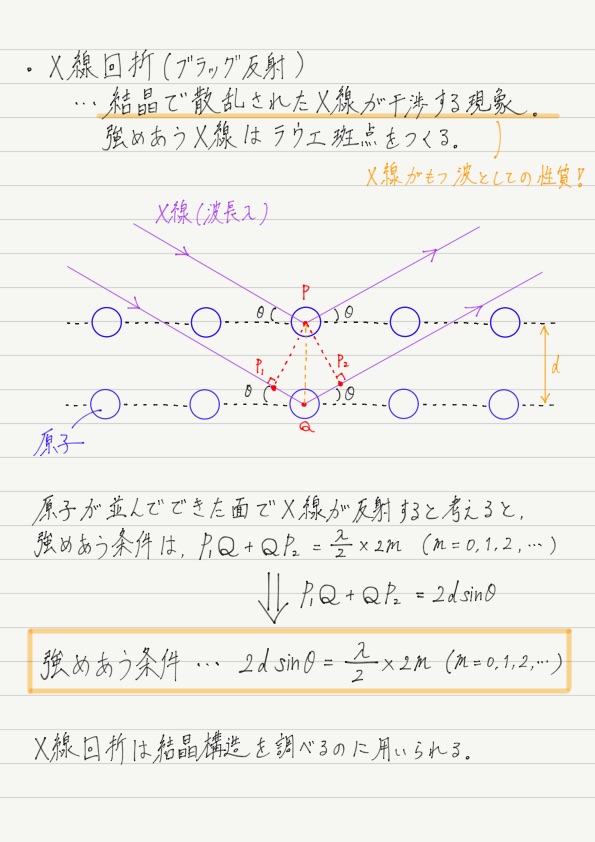
結晶内の規則正しく並んだ原子にX線を照射すると,X線は原子によって散乱されます。
注意深い人だと,「急に散乱? 回折の話はどこいった?」というリアクションをとってくれると思いますが(笑),X線を結晶に当ててラウエ斑点が現れる現象では,回折と散乱がだいたい同じ意味で使われているようです。
なので,「X線が結晶により散乱されて〜」という文章は,「X線が結晶により回折されて〜」と読み替えてOKです。
さて,散乱されたX線がうまいこと強めあうのはどのような条件を満たすときでしょうか?
この条件はブラッグ親子によって明らかにされました。 彼らによれば,
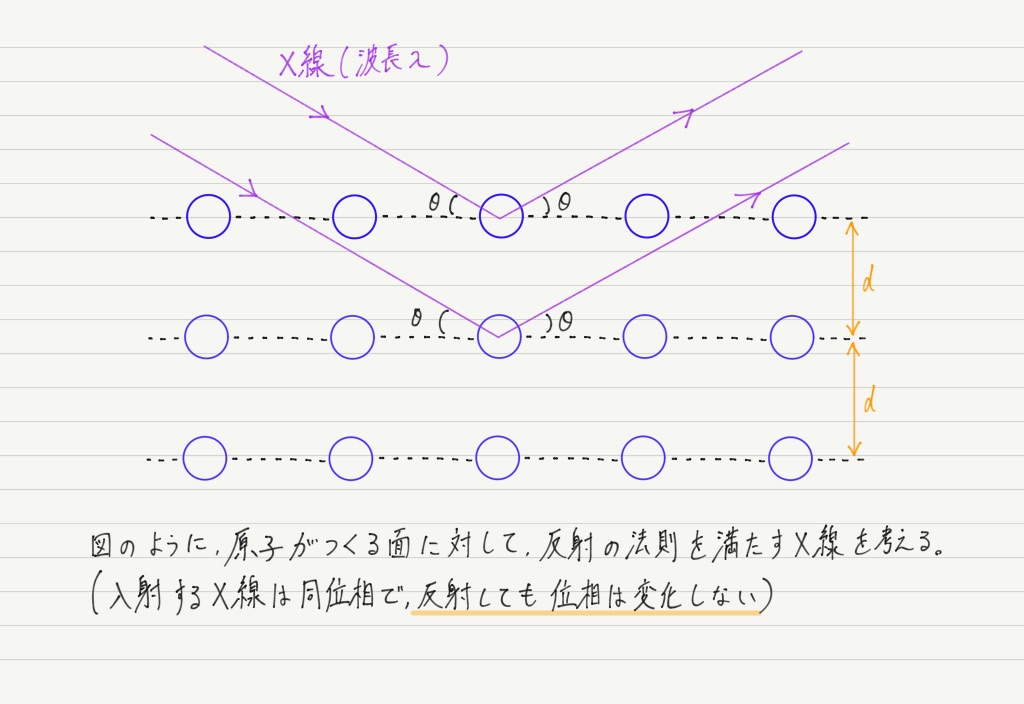
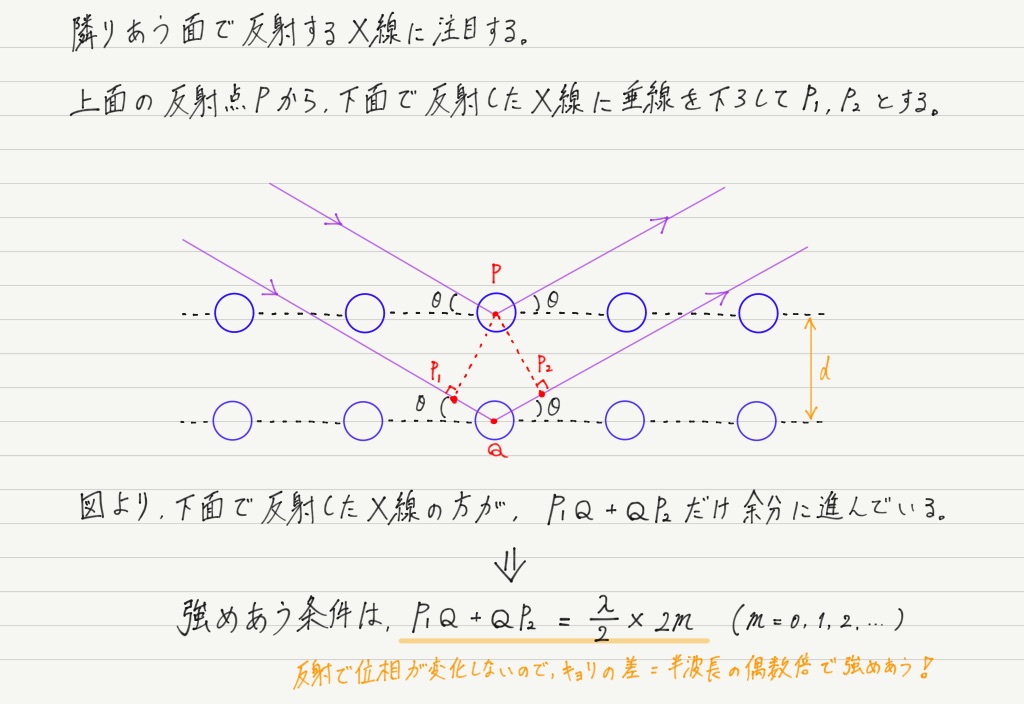
① X線はさまざまな方向に散乱されるが,反射の法則を満たす方向で強めあう。
② 隣りあう面で反射されたX線どうしが同位相で重なるときに強めあう。
だそうです。 うーん,文章で書かれても微妙ですね…
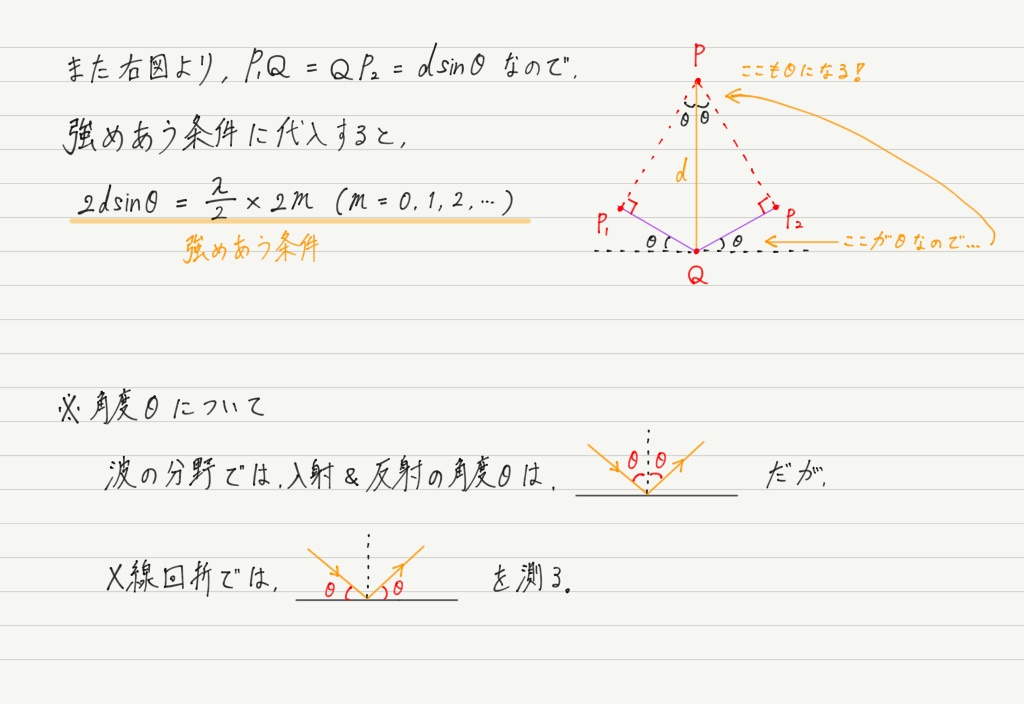
波の干渉のときは明線条件を式で表していたので,今回も図を書いて強めあいの条件を式の形で表してみましょう!
X線 “回折” という名前とは裏腹に,反射を用いて強めあう条件を求めました。
このことからX線回折は別名「ブラッグ反射」とも呼ばれます。
いま求めた強めあいの式の最大のポイントは式の中に原子間隔dが含まれていること!
よって原子間隔がわかっている結晶を使って実験を行えば,この式からX線の波長が求められます。
逆に,波長がわかっているX線を使って実験をすれば原子間隔を求めることができ,結晶構造を調べる手がかりになります。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
光は波の性質だけでなく粒子としての性質も兼ね備えていました。
…もしかしてX線も??