今回から最終講までの4回は,ひたすら光の干渉について勉強していきます。
よく出題されるのに苦手とする人が多い,そんな印象の分野です。
苦手な人に共通して言えるのは,式を暗記して済まそうとしていること。
光の干渉条件は導出をきっちりできないと応用が効かず,意味がありません!
現象の理解に努め,「どうやって式が得られるのか」に注目して読み進めてほしいと思います。
物体と波のちがい
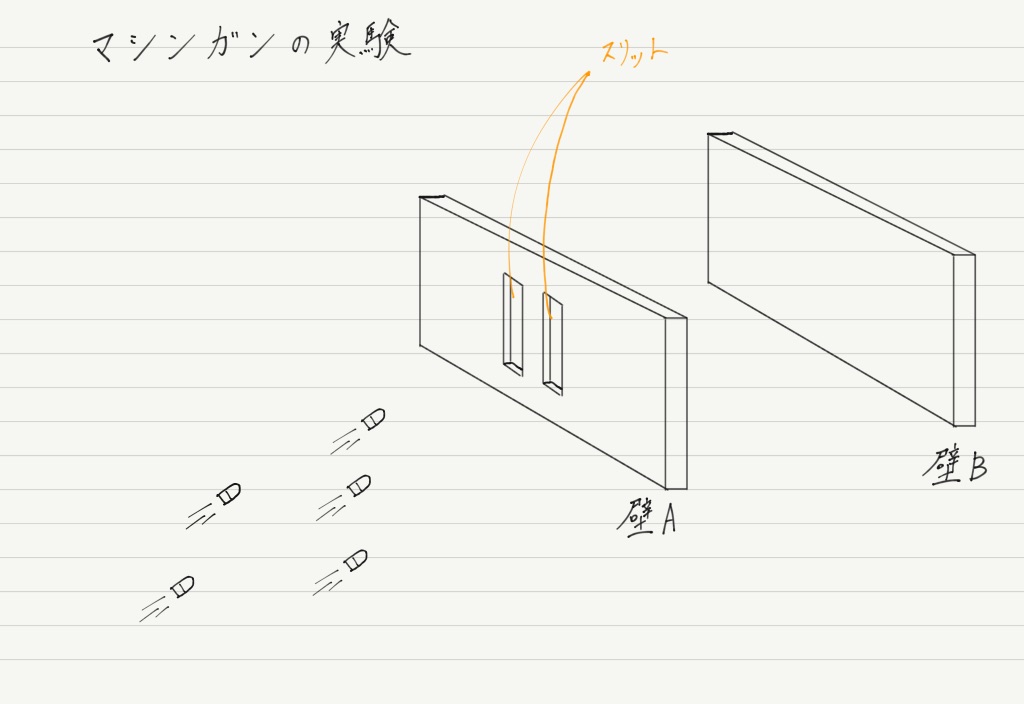
突然ですが,2つの細長い穴(スリットという)がある鋼鉄の壁Aに向かって,マシンガンを乱射する様子を想像してください。
ほとんどの銃弾は壁Aに遮られますが,いくつかの銃弾はスリットを抜けて,向こう側の壁Bに着弾します。
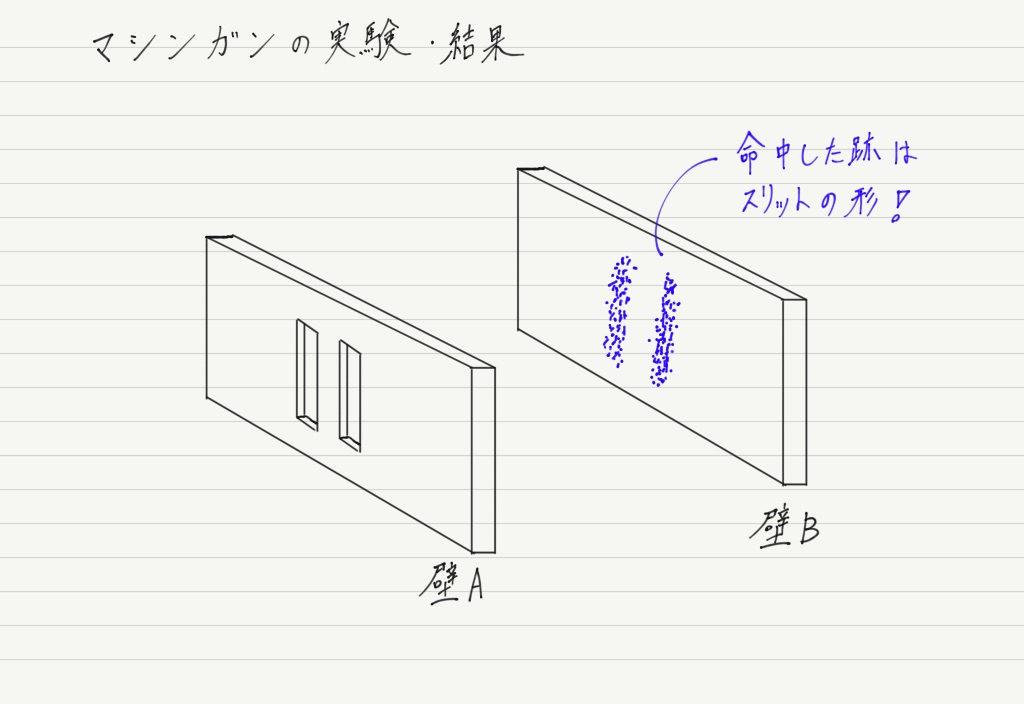
このとき,壁Bについた銃弾の跡は次のようになるはずです。
実際にマシンガンを準備して実験するまでもなく,この結果は明らか!
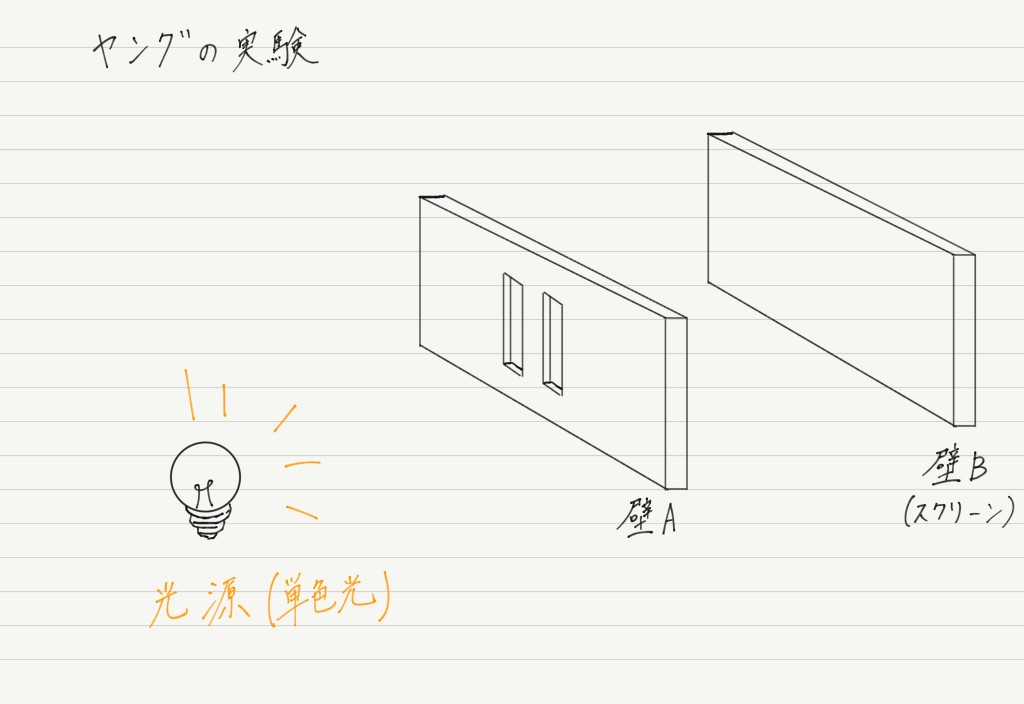
さて,今回のタイトルにもなっている「ヤングの実験」とは,いまマシンガンでやったことを光に変えて行う実験のことです!
つまり,2つのスリットが空いた壁に向かって光を当てるだけ。
問題はスクリーン上がどうなるか。
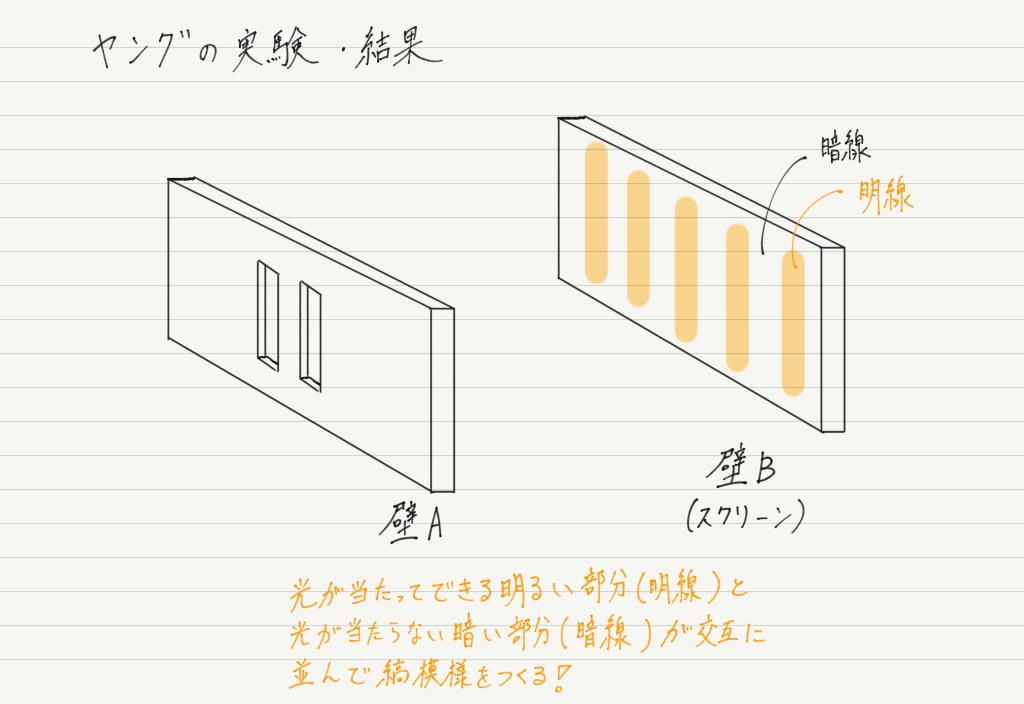
光が当たる部分は明るくなり,そうでない部分は暗いままなわけですが…
なんと!銃弾の場合とまったくちがう模様が出現します!!
これは一体どういうこと??
回折と干渉
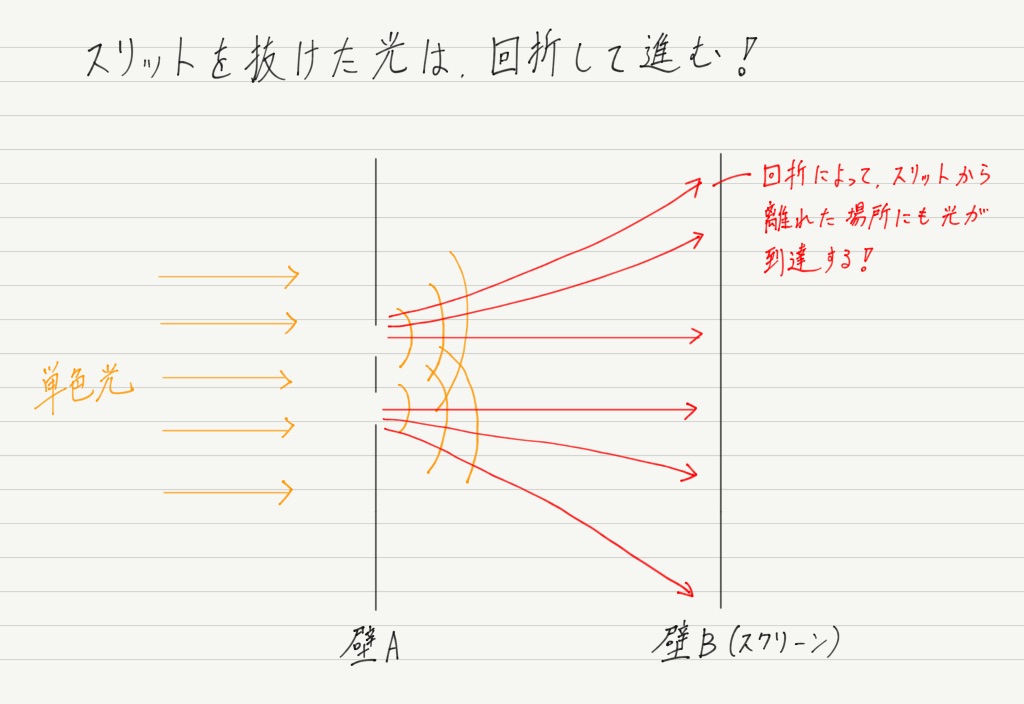
この実験結果のちがいは,銃弾は真っ直ぐにしか進めないが,光は回折によって拡がって進むことに由来します。
そう考えれば,銃弾だと届かなかった部分が,光だと明るくなるのも理解できます。
問題は,なぜ明るい部分と暗い部分があるのかということ。
回折して進めるのなら,全体が明るくなるはずではないでしょうか?
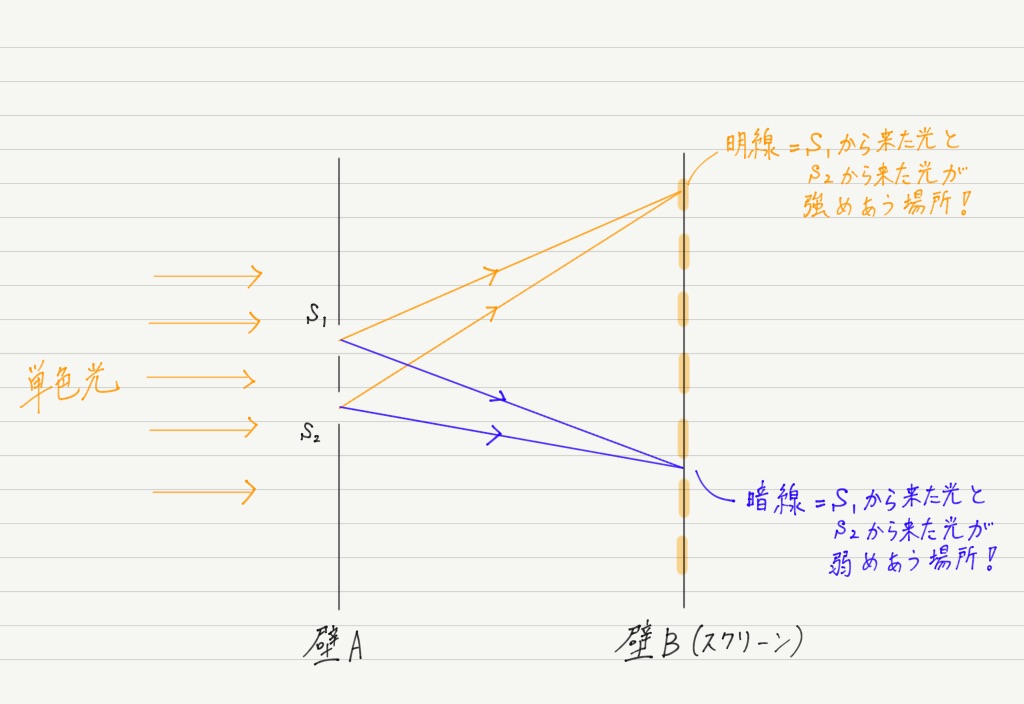
この疑問を解決するのが,波の干渉です。
2つの波源から波が出るとき,波源からの距離に応じて,強めあう場所と弱めあう場所が存在するのでした!
つまりヤングの実験とは,波の干渉の光バージョンに他なりません。
というわけで,ここから先は波の干渉の知識を使って計算を進めていきます。
強めあう条件・弱めあう条件が理解できていない人は,波の干渉の記事をよく読んでから出直してきてください。
大丈夫だよ!という人は計算へGO!
明線条件と暗線条件
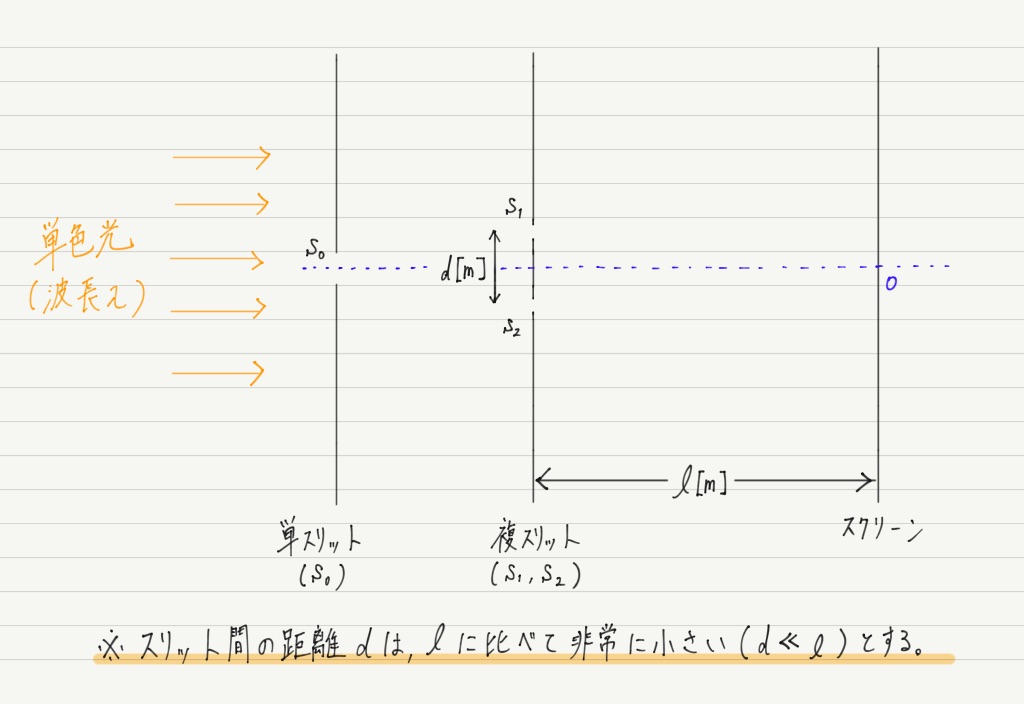
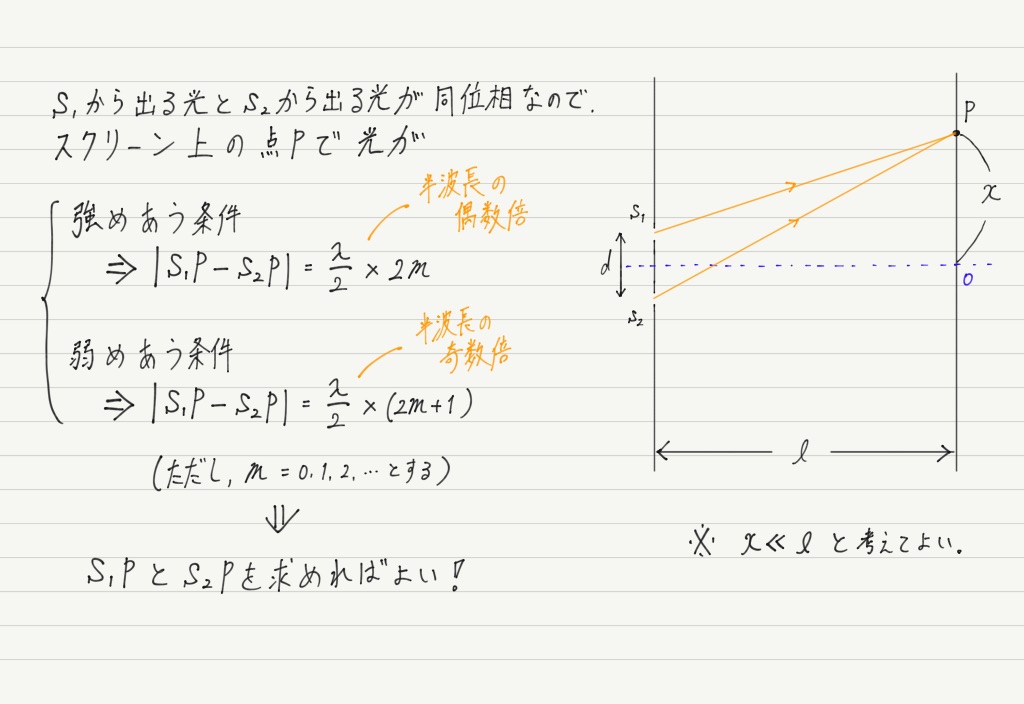
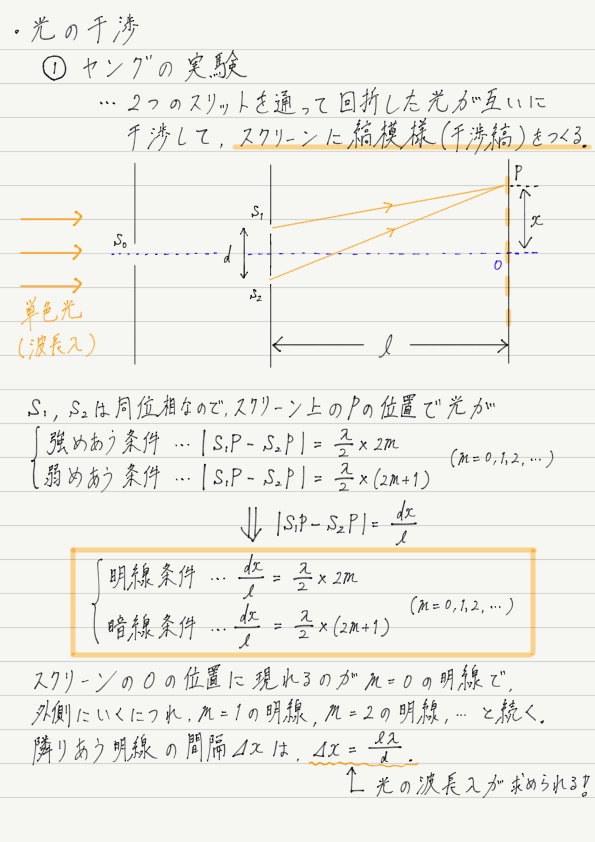
ヤングの実験を以下のような設定で行います。
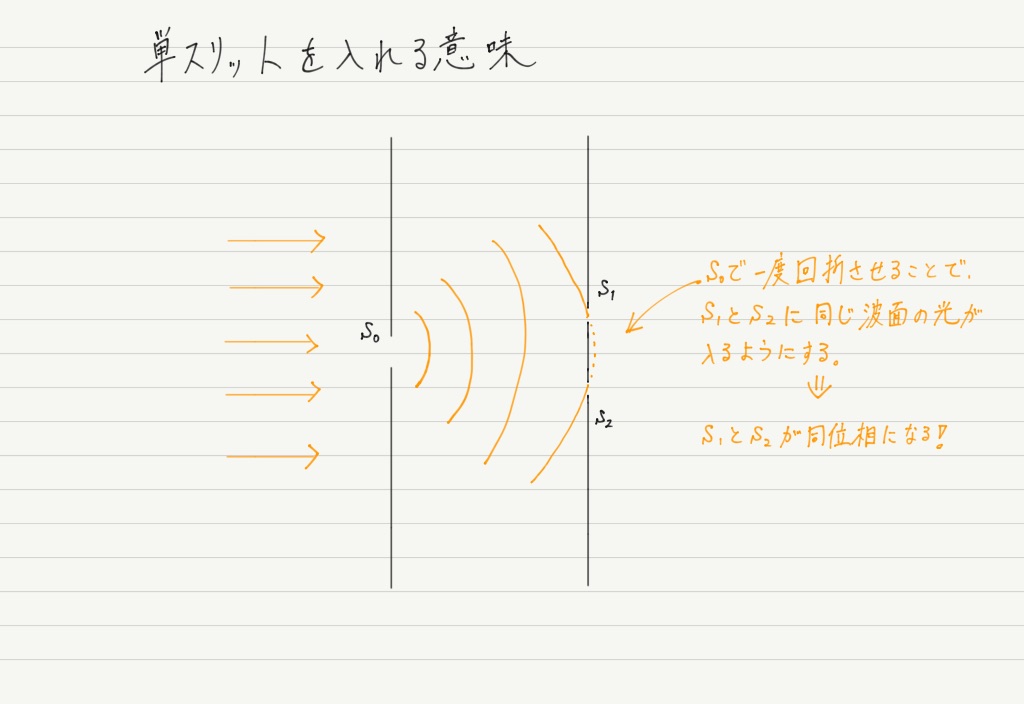
光源と複スリットの間に単スリットを入れてあるのは,2つのスリットに入るときの光の位相を揃えるためです。
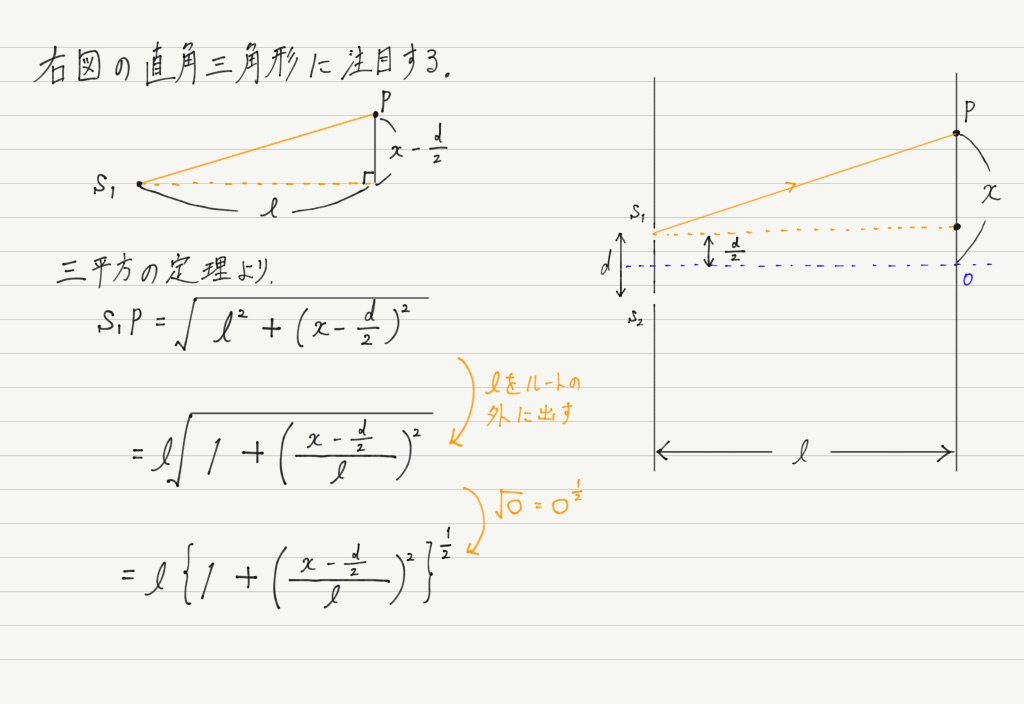
それではスクリーン上のどこが明線 or 暗線になるのか,干渉条件をもとに探っていきましょう。
けっこう長丁場なのでがんばってついてきてください。
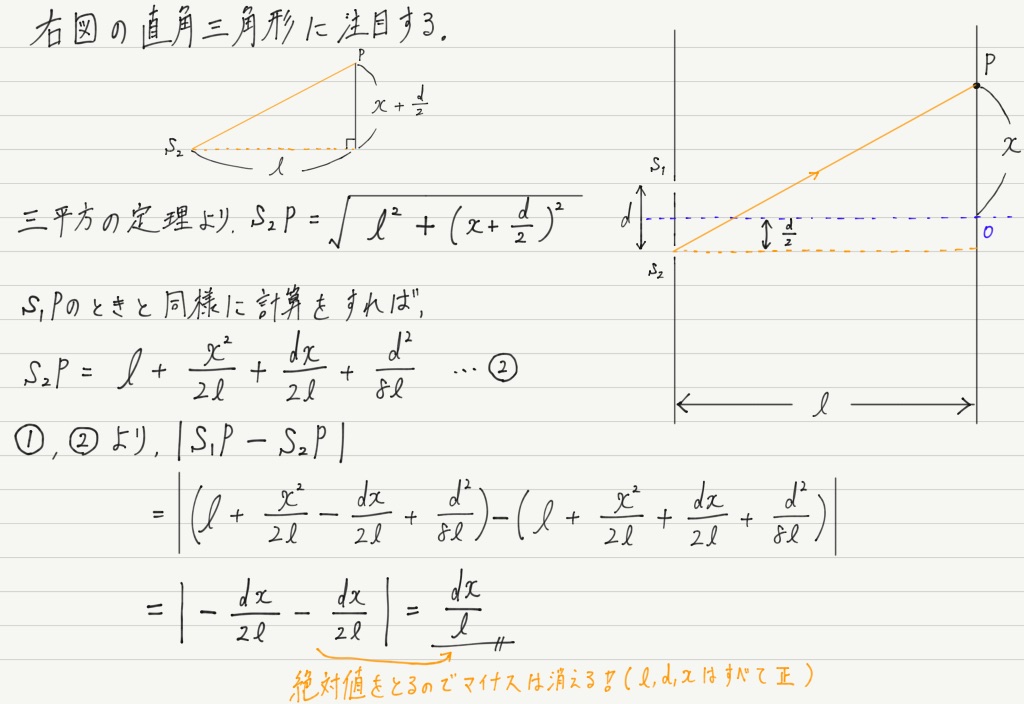
ふぅ,お疲れ様です。
これで2つのスリットからスクリーン上の座標xの点までの距離の差が求められました。
これで明線が現れる場所と暗線が現れる場所が特定できます!
(※ 暗線が話題になることはあまりないので,以下では明線に絞って話をしていきます。)
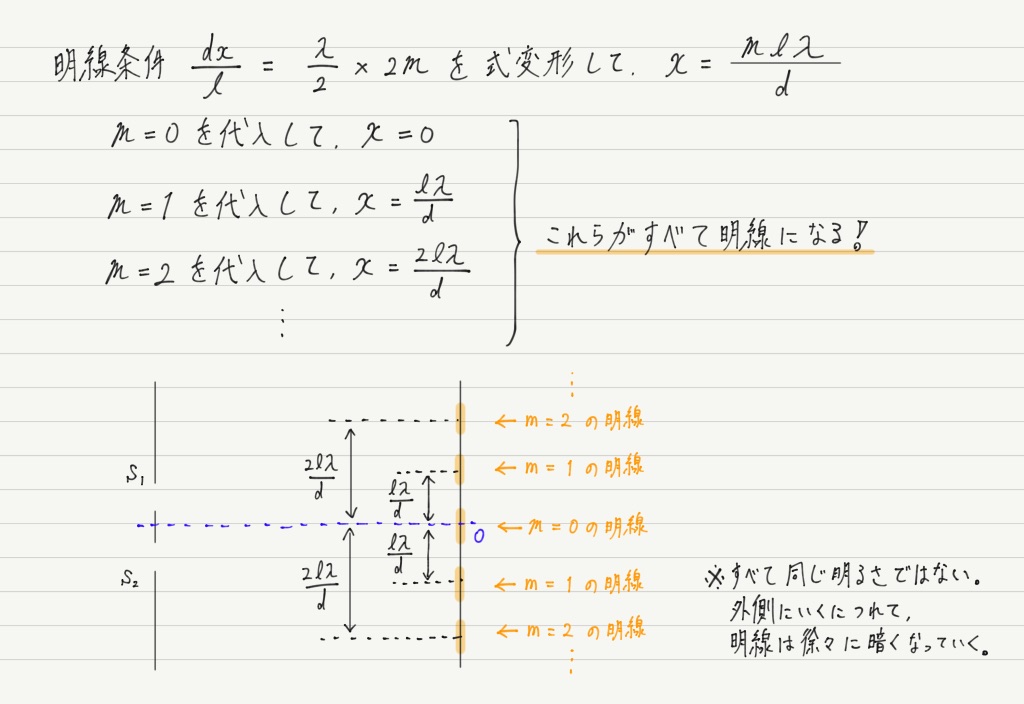
さて条件がわかったので,具体的に明線が現れる位置を求めてみましょう!
明線どうしの間隔も上の図を見れば明らかですが,一応計算しておくと,
今回扱ったのは一番シンプルなヤングの実験です。
これが入試問題になると,光源の位置を変えたり,スリット手前にガラスを入れたり,実験装置全体を液体で満たしたりとやりたい放題。笑
問題の設定が変われば明線条件も変化するので,式の丸暗記は役に立ちません。
しかし,「明線条件は光源からの距離の差を計算して得られる」ことが分かっていれば,問題を多少いじられても対処できるはずです。
まずはもう一度自分で今回の明線条件を求めてみる,それができたら問題集でちょっとひねった問題をやってみる。
どんどん練習を積んで,光の干渉の苦手意識を払拭しましょう!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
ヤングの実験以外の光の干渉についても理解を深めていきましょう。