波の分野の山場のひとつである干渉。
できない人の多くは「強めあう条件は言えるけど,イメージができない!!」と言います。
何でもかんでもイメージに頼るのはよくないですが,波の干渉に関していえば,ちゃんとイメージできるようになったほうが有利です。
「正しくイメージができるようになること」を目標に読み進めてください!
波の干渉とは
重ねあわせの原理や定常波のところで学習した通り,波どうしは重なって合成波をつくります。
山と山(または谷と谷)が重なり,大きな山(谷)になることを,波どうしが「強めあう」と表現します。
逆に,山と谷が重なって,振動が小さくなることを,波どうしが「弱めあう」と表現します。
波の干渉とはこのように,波どうしが重なって強めあったり弱めあったりする現象のことをいいます。
定常波は波の干渉の1つの例です。 定常波では「腹」が強めあう点,「節」が弱めあう点,ということになります。
定常波と聞いてピンとこない人はちゃんと復習しましょう。
イメージするためのポイント
ここからが本題(まずは強めあう点に絞って話を進めます)。 波が強めあう点というのは限られています。
なぜなら,強めあうには山と山(または谷と谷)がぴったり重なる必要があるからです。
2つの波があるとき,ちょうど山どうし(谷どうし)が重なる点というのはそう多くはありません。
では,例題をもとに,強めあう点がどこにあるか考えていきましょう。
説明に入る前に,波の干渉をイメージするためのポイントを伝授しておきます。
ポイントその①,波の山と谷だけに注目すること。
グラフの読み取りや定常波だったら,山と谷以外の点(例えば振幅が0の点)もそれなりに注目する必要がありますが,強めあいや弱めあいでは山と谷の位置だけが問題なのでそれ以外は必要ありません。
ポイントその②,波を止まっているものとして考えること。
波自体は波源から遠ざかるように進みますが,強めあう点や弱めあう点は移動しません。
これまた定常波を思い浮かべてください。 定常波は振動はしていますが,腹と節は常に定位置にあります。
干渉によって強めあう点と弱めあう点もこれとまったく同じです。
移動しているものより止まっているもののほうが考えやすいので,波のy-xグラフを書いたときと同様に “時間を止めて” 考えていきます。
強めあいの条件を探る
では先ほどの例題に戻りましょう。
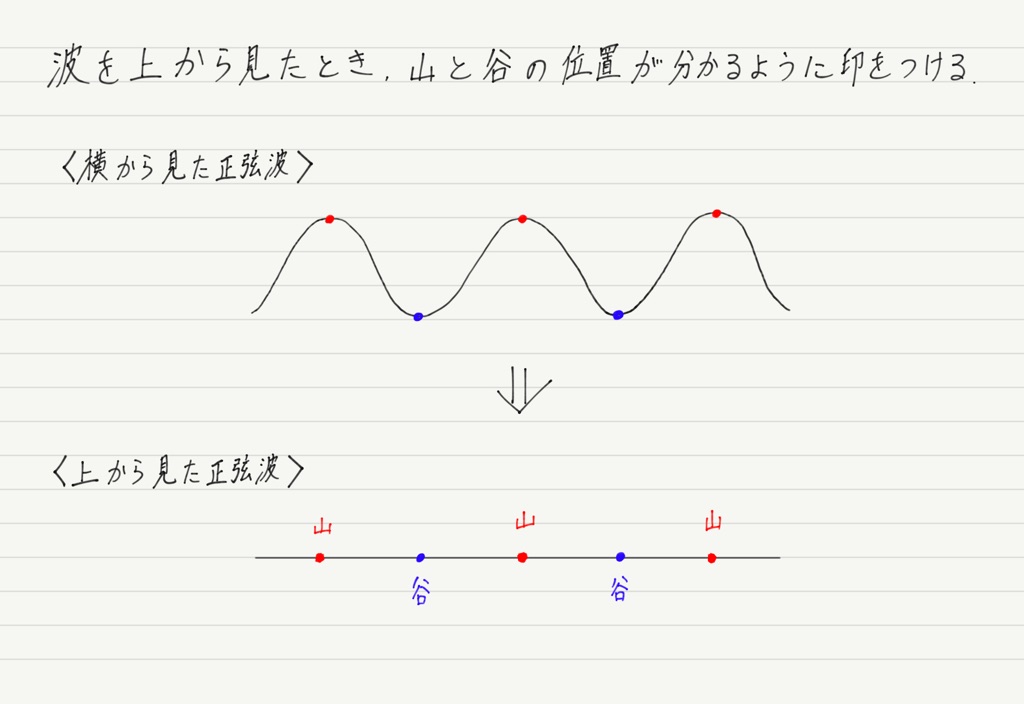
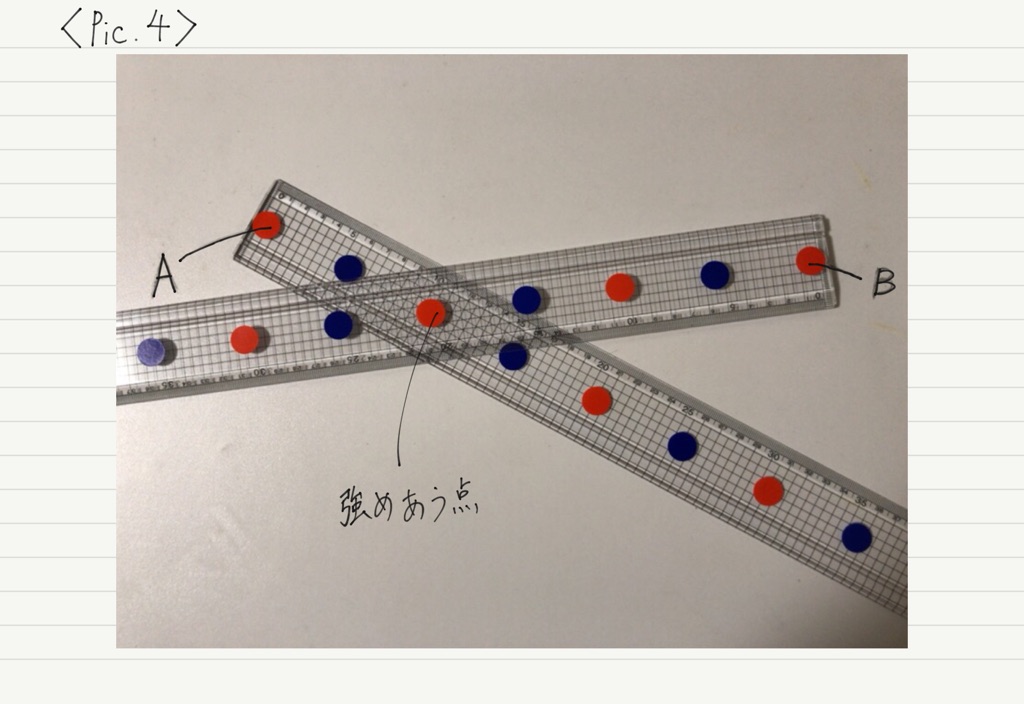
波を上から見た図が必要なので,波の山を赤い点,谷を青い点にして表すことにします(ポイントその①で述べたとおり,山と谷だけが分かれば十分)。
当たり前ですが赤い点と青い点は交互に,等間隔に並びます。
では,赤い印と青い印を交互に等間隔に付けた棒を頭の中にイメージしてください。 みなさんがイメージしやすいように実際に作ってみました↓
波はAとB両方から出るので,棒は2本必要です。
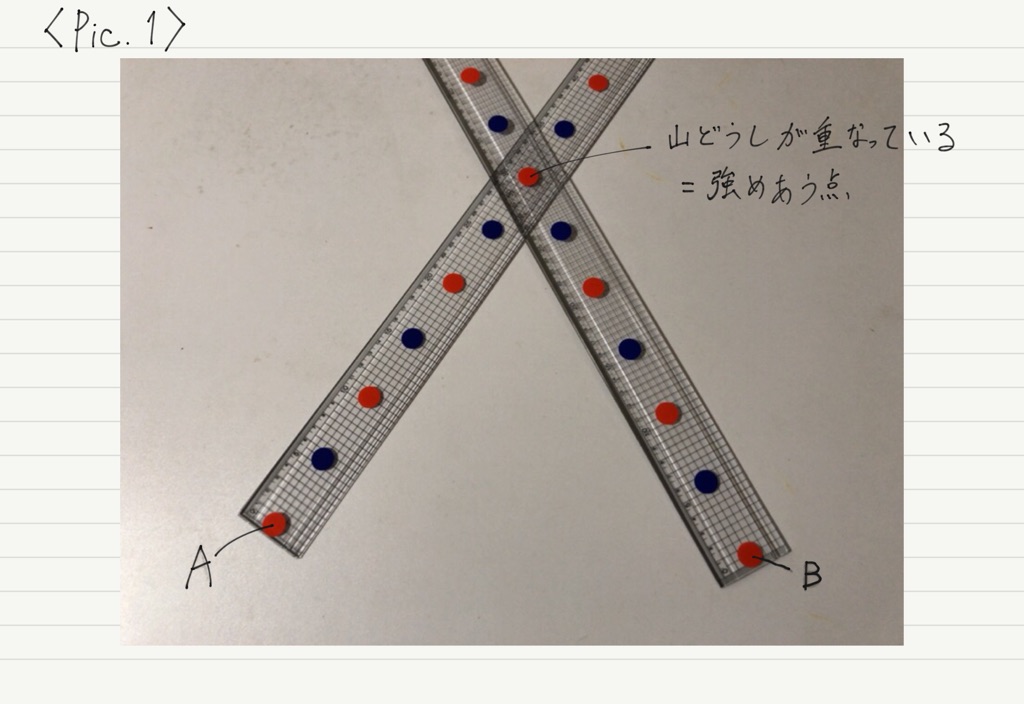
さて,今回波源A,Bは同位相なので,片方が山を出しているとき,もう片方の波源も山を出しているということになります。 よって,それぞれの波源に用意した棒の赤い印を重ねます。
もちろん波源は振動しているので,A,Bがいつまでも山の状態というわけではありませんが,ポイントその②で述べたとおり,強めあう点を見つけるだけなら波は止まっているものとして考えて問題ないので,波源のところは山ということで固定しておきます。
次に,山と山,もしくは谷と谷が重なる点を探していきます。
波は波源から360°全方向に広がって進むので,波源に赤い印を重ねたまま棒を回転させてみましょう。
2つの棒を回転させて,同じ色の印どうしが重なる点こそ,我々の探している強めあう点です!!
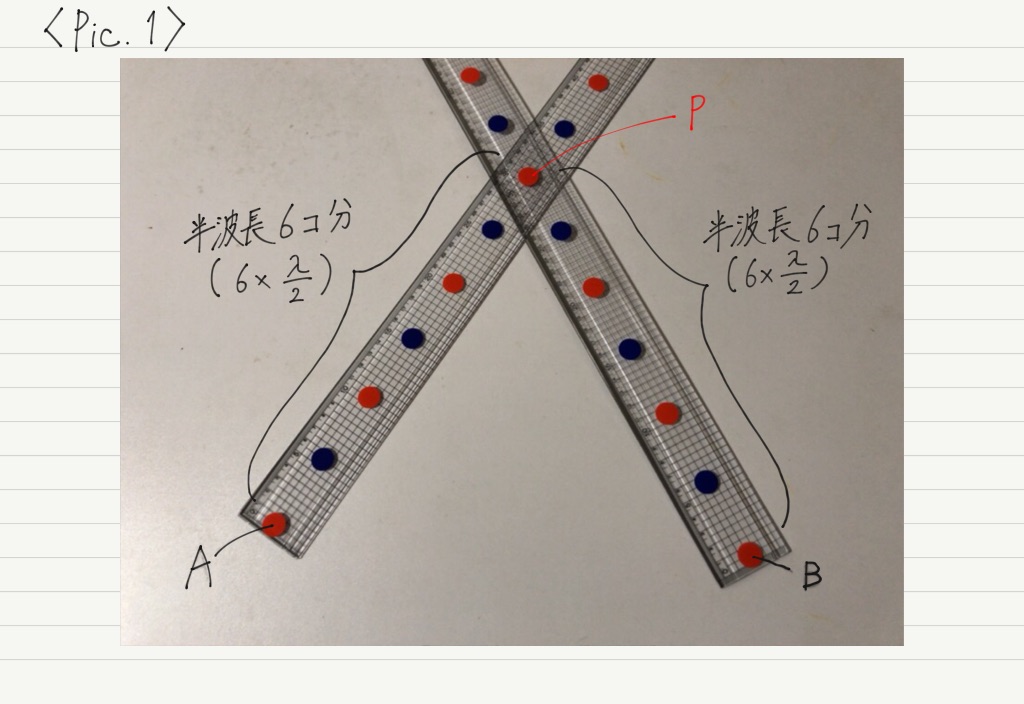
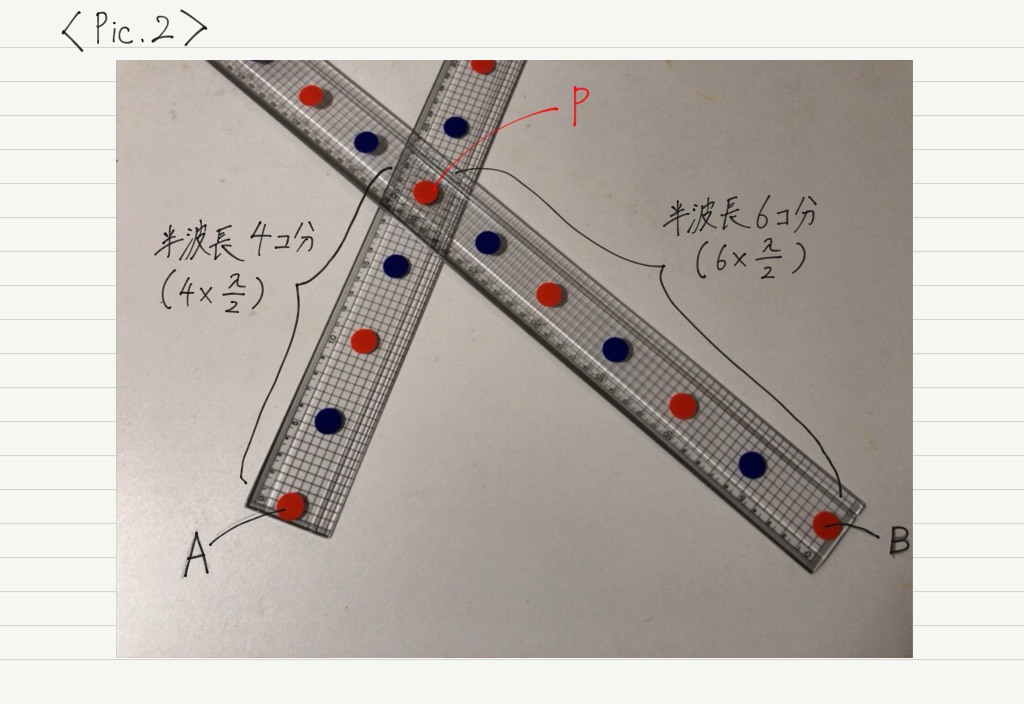
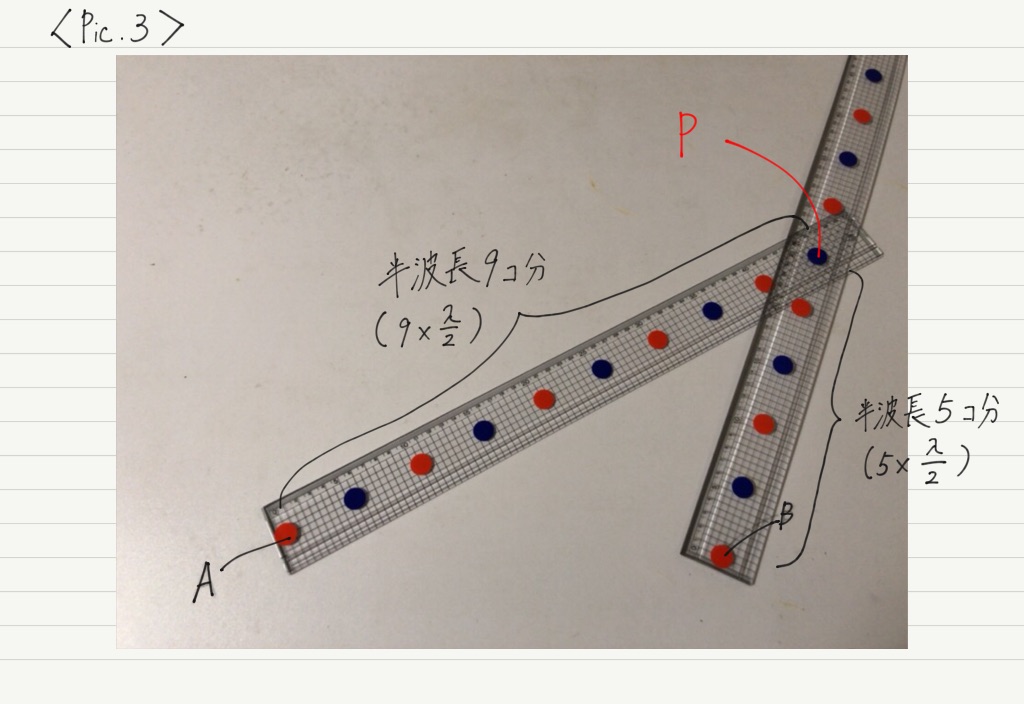
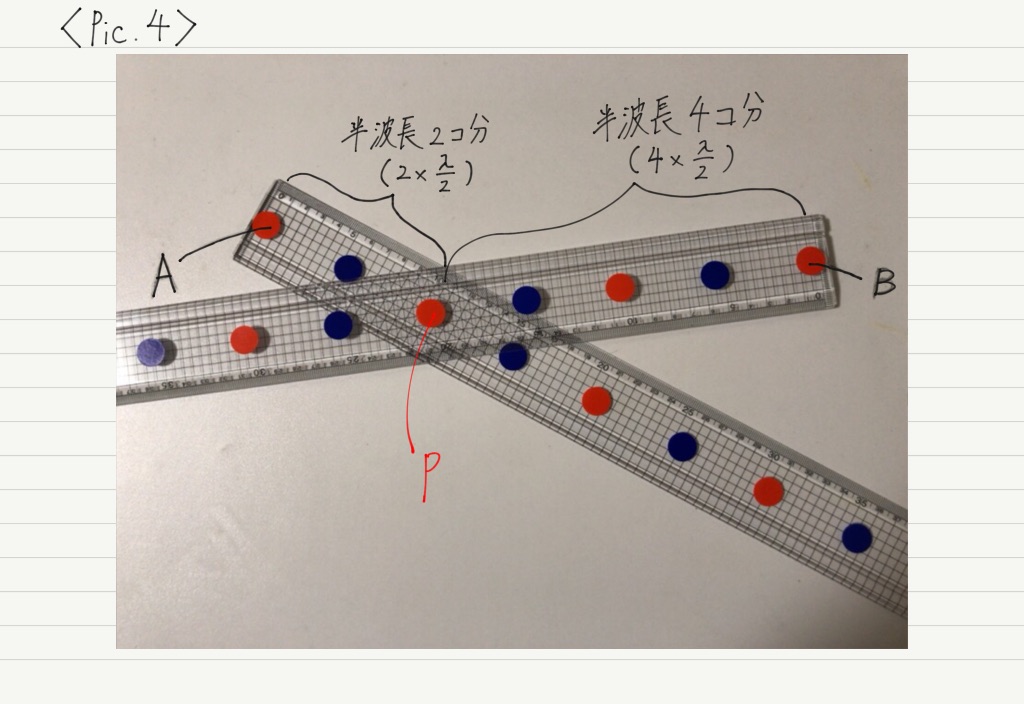
では,Pic.1〜4で,波源から強めあう点(点Pとする)までの距離を測ってみます。
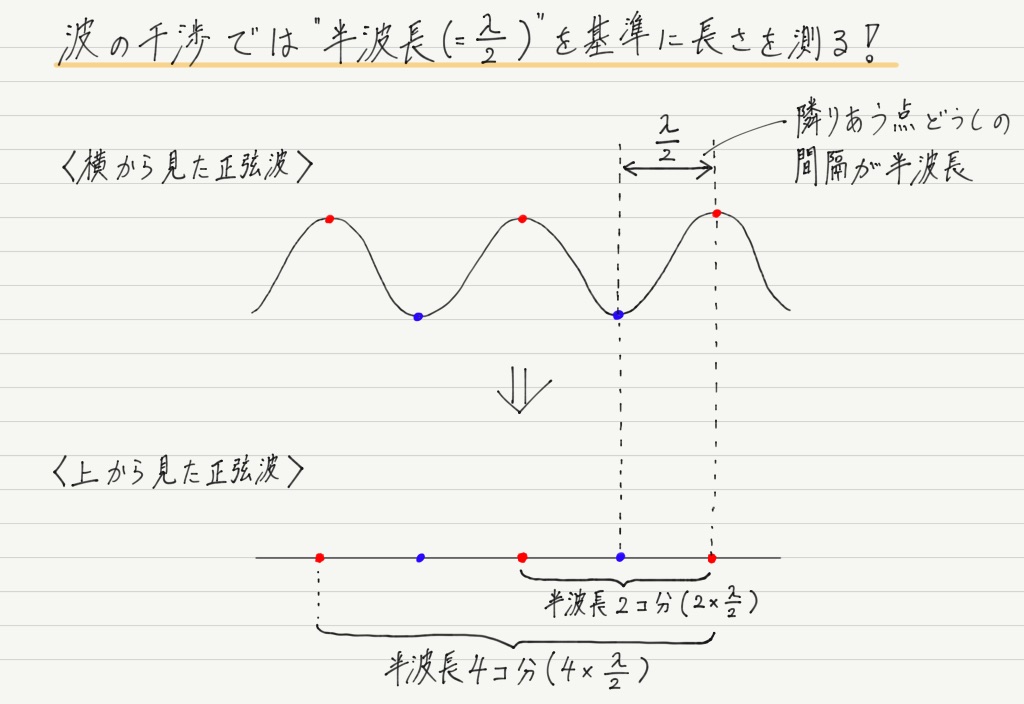
ただし,普通に何cm,何mと測るのではなく,波長を使って距離を測っていきます。
では実際に,「波源A,Bから強めあう点Pまで,半波長◯個分」というように表してみましょう!
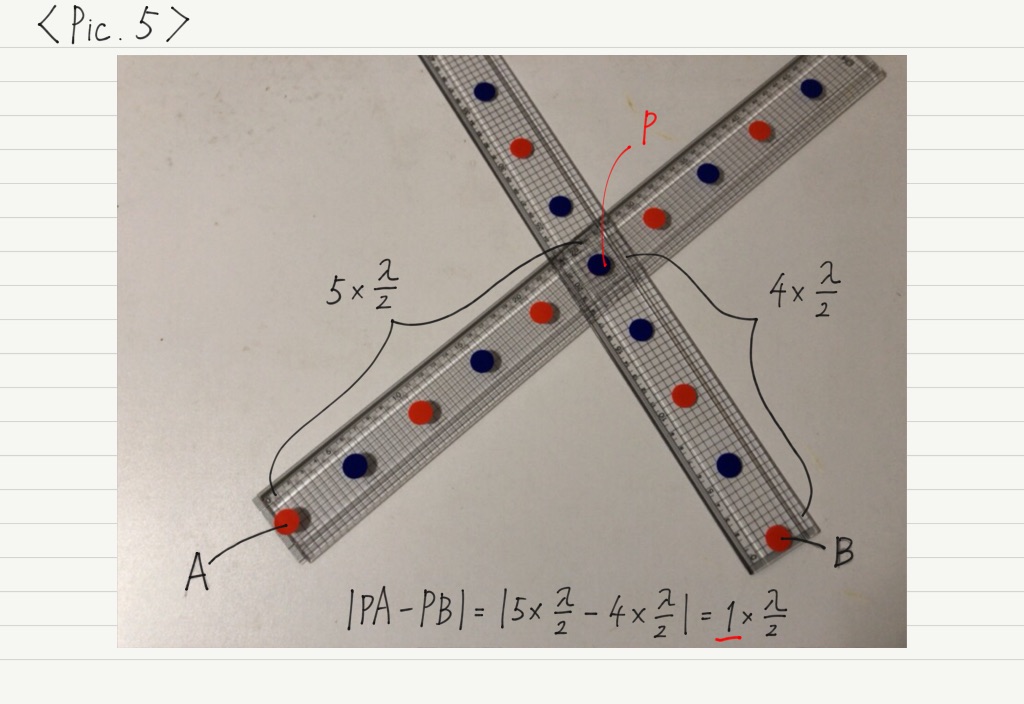
Pic.1の場合,2つの波源から等距離にある場所なので,同位相で重なるのは当然です。
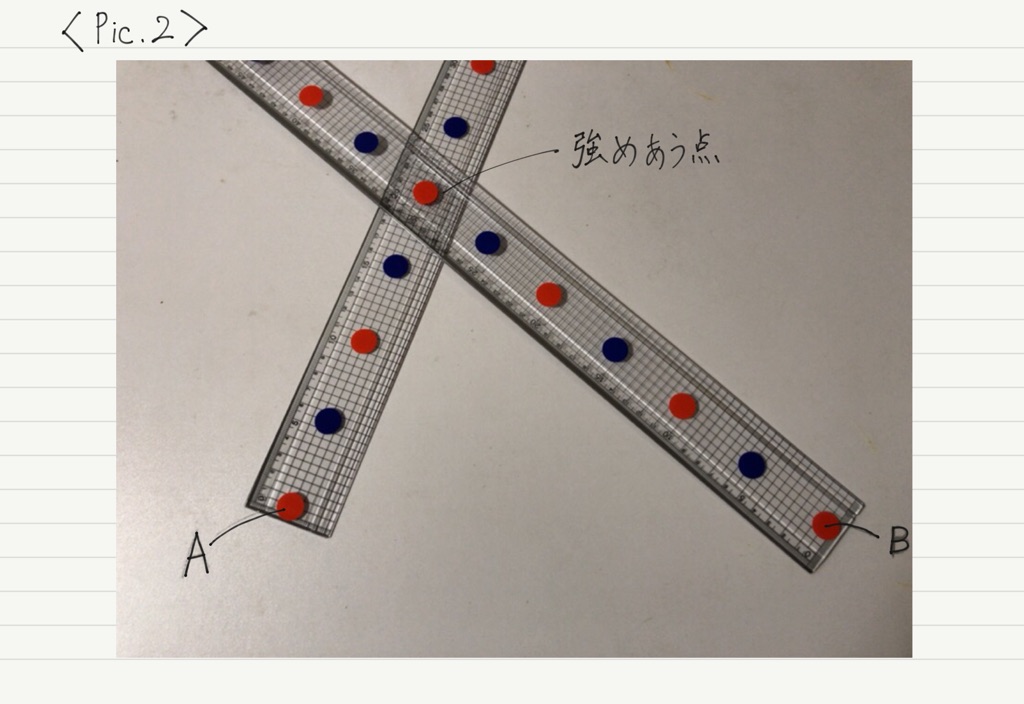
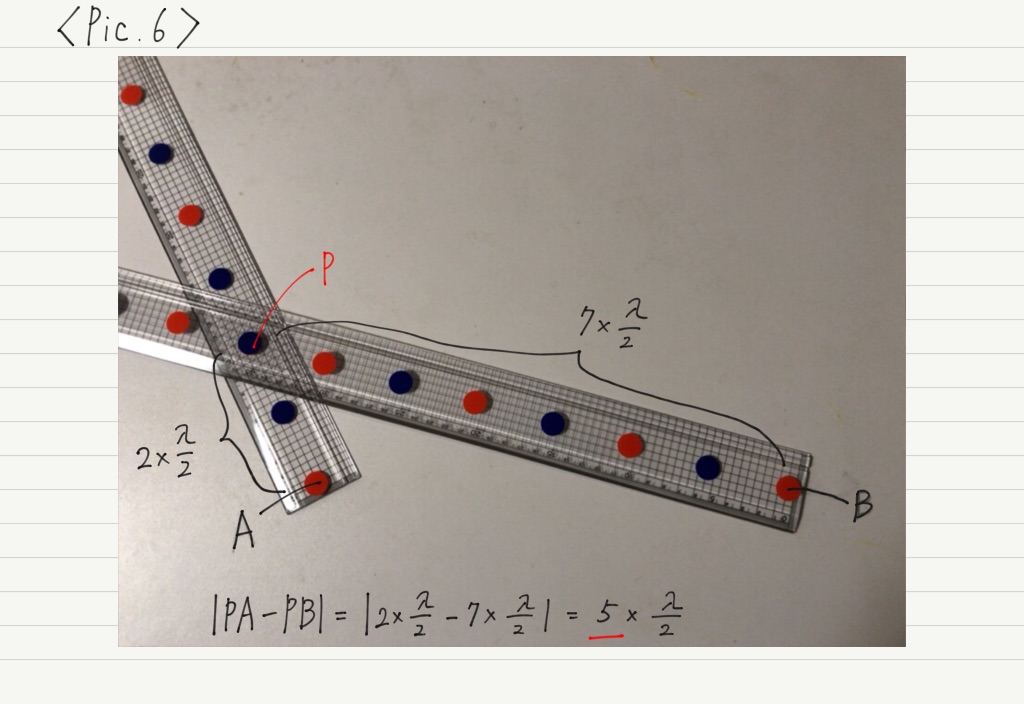
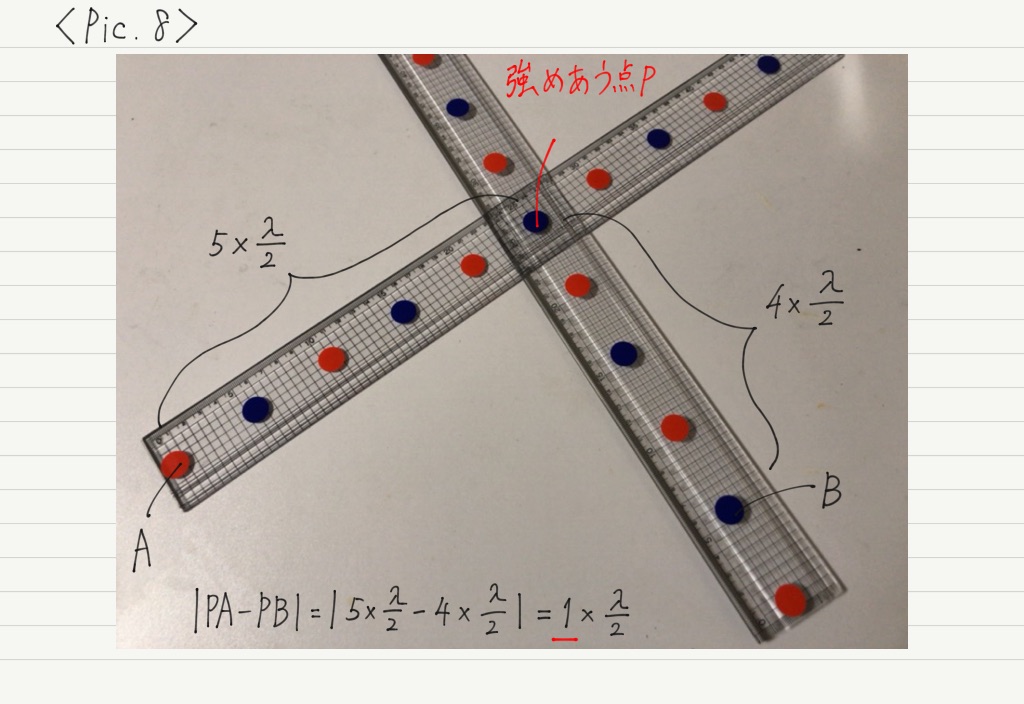
しかし,Pic.2〜4のように異なる距離にある点では,遠い方の波源からやってくる波が “余分に” 進まないといけません。
では,その “余分な” 距離を計算してみましょう。
2つの波源からPまでの距離の「差」を求めればいいですね。
先に結論を書いてしまいましたが,「余分に進まないといけない距離」がちょうど半波長の偶数倍になること。
これが強めあいの条件になります。
なぜなら,半波長2個(=1波長)おきに波は同位相になるからです。
なので,「余分に進む距離=半波長×偶数」のとき,先に到着していた波と再び同位相になって出会うことになります。
教科書に書いてある「強めあう条件」はこのようにして導かれるのです!
弱めあう条件はどうなるか
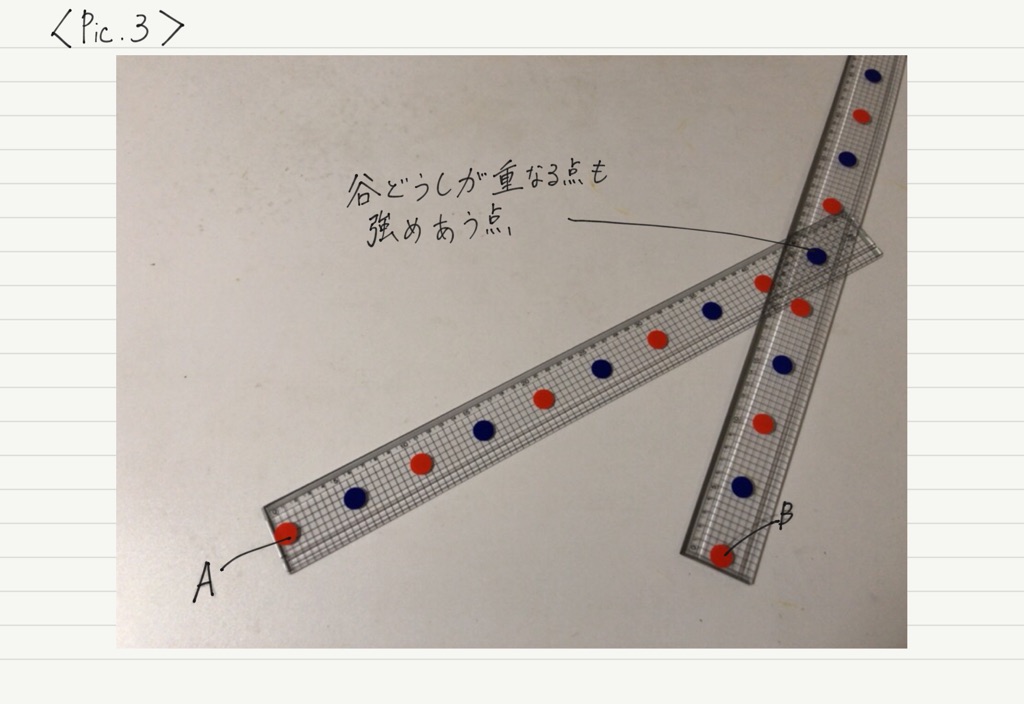
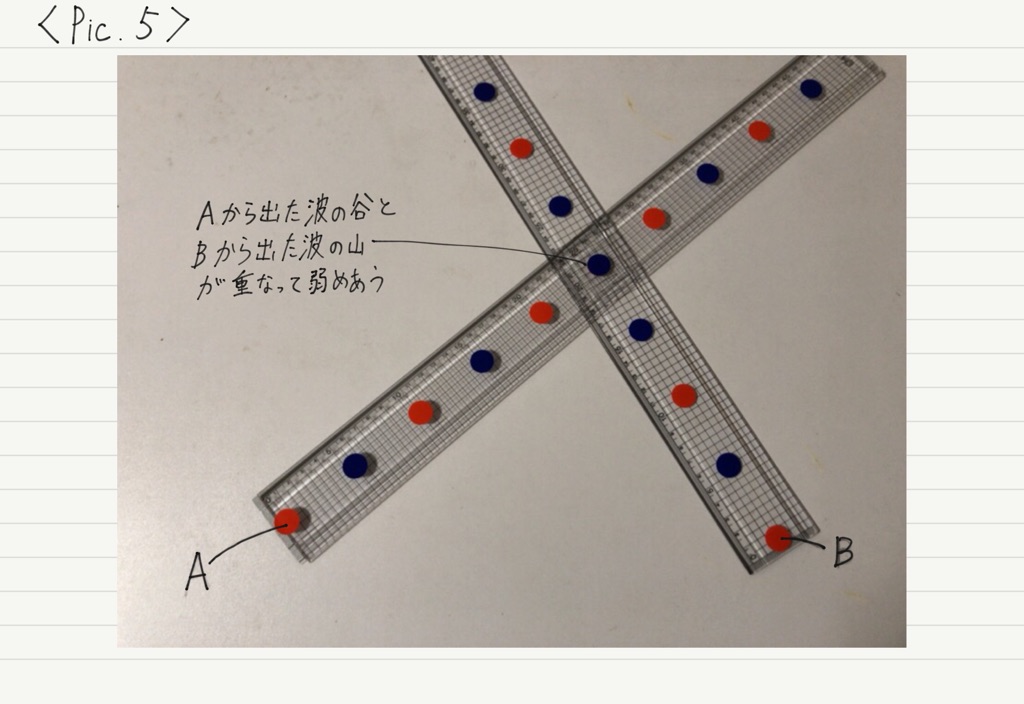
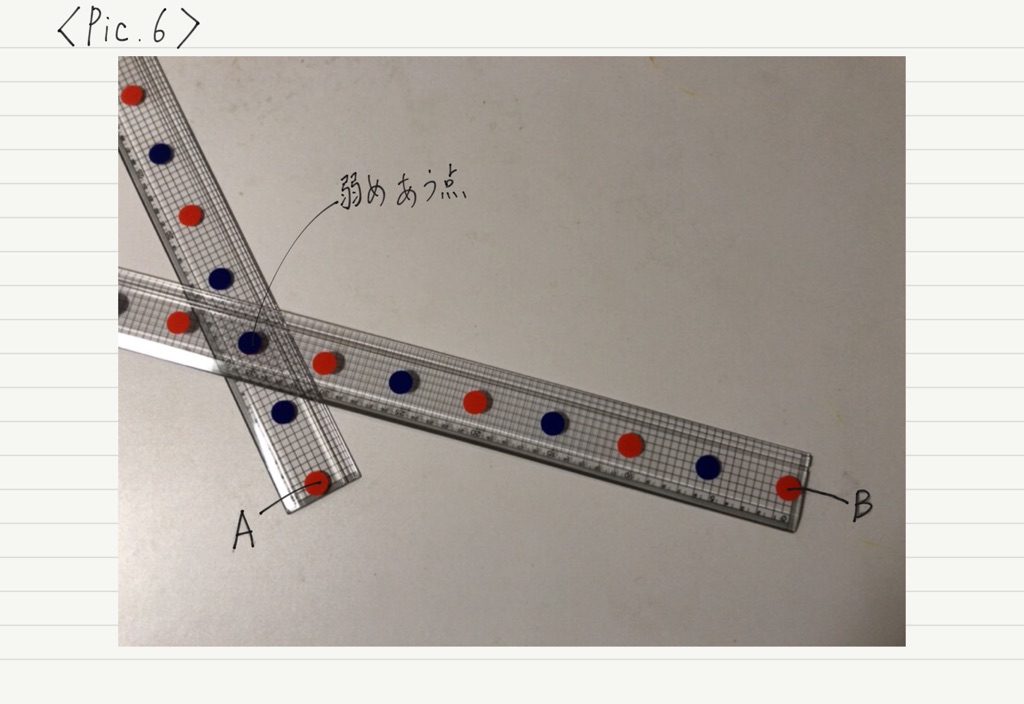
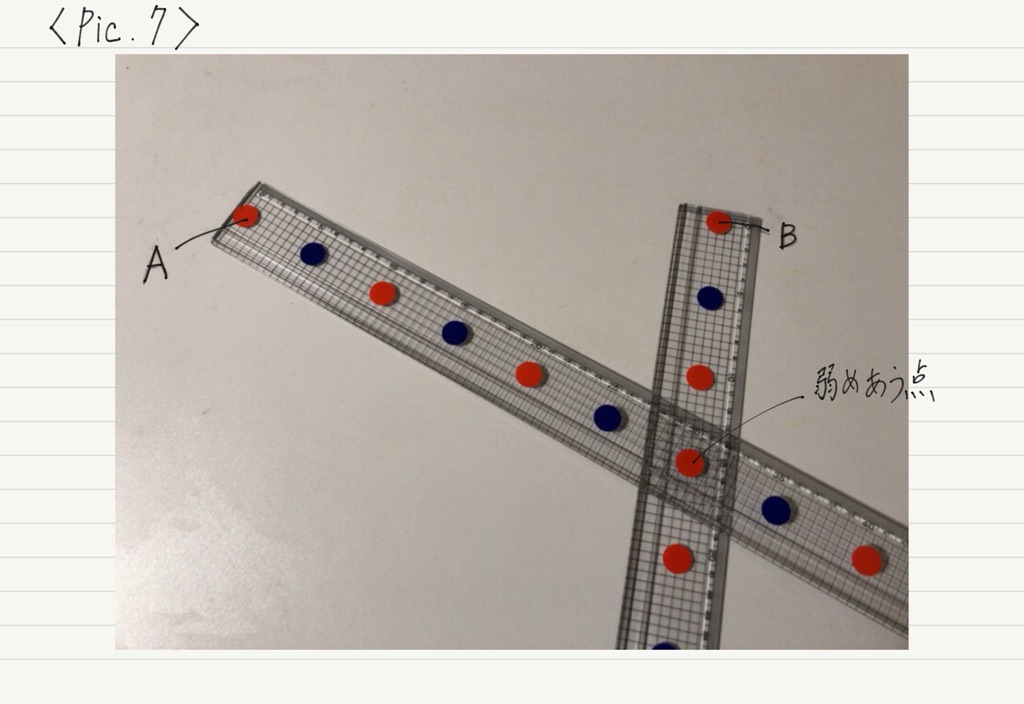
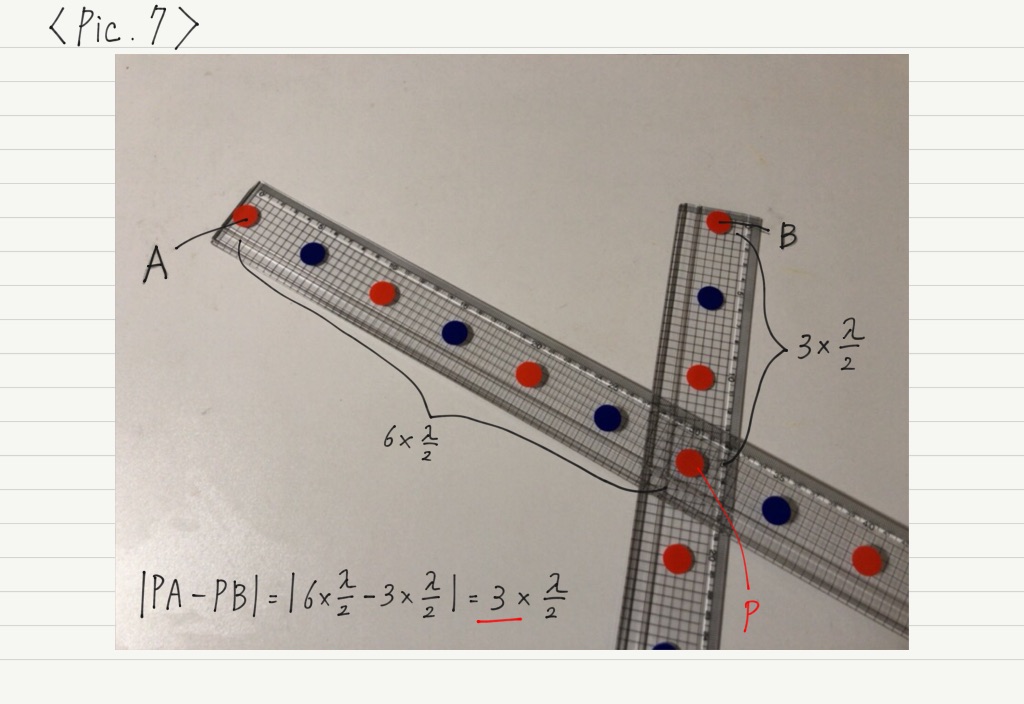
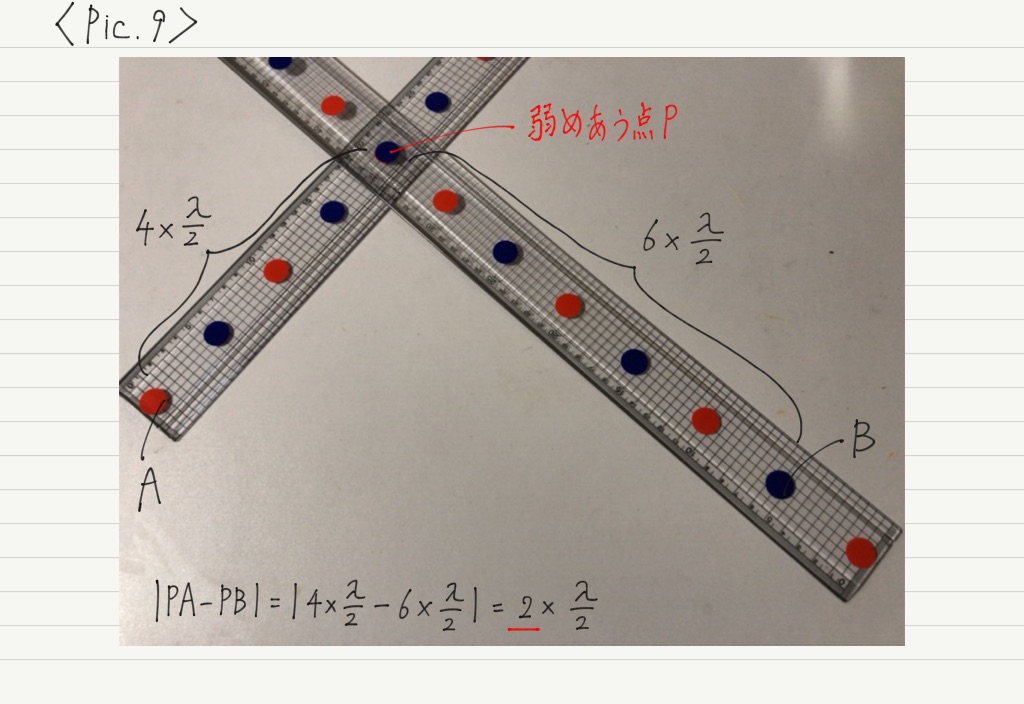
次に弱めあう条件を探っていきましょう。 異なる色の点が重なる場所が,干渉によって弱めあう場所になります。
弱めあう点をPとして,先ほどと同様にPAとPBの距離の差を計算してみると,
PAとPBの距離の差が,半波長の奇数倍になっていることがわかります。
赤い印から数えて,逆位相である青い印は1個,3個,5個,…おきに現れるため,「余分に進む距離=半波長×奇数」のとき,先に到着していた波と逆位相になって出会うことになります。
これで「弱めあう条件」も導くことができました!
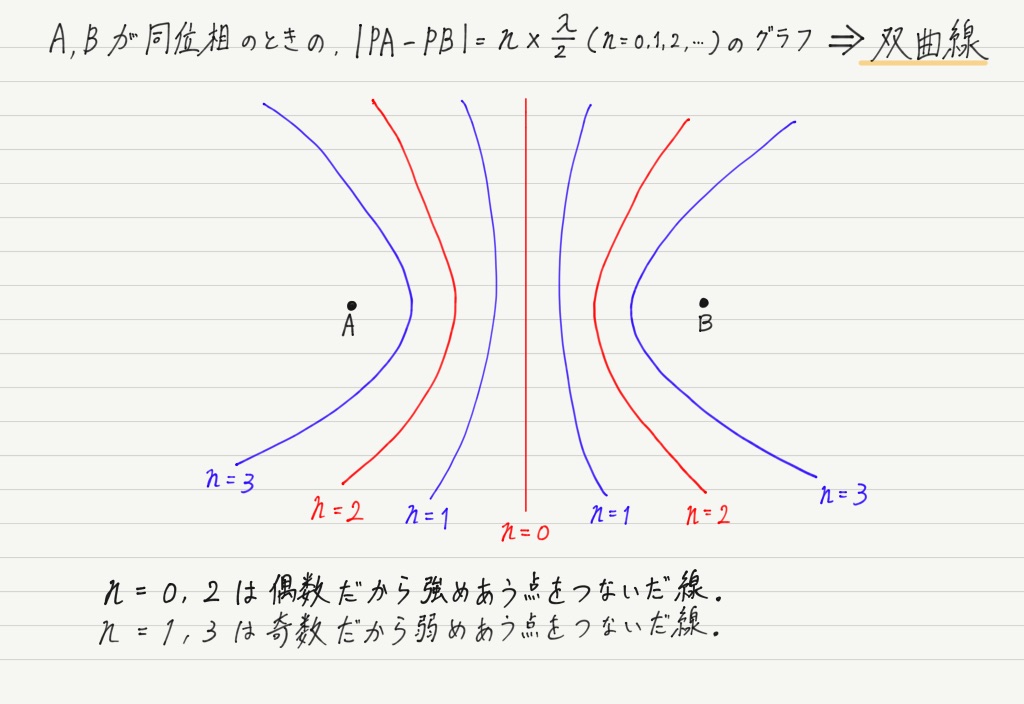
強めあう点と弱めあう点が存在する場所
上の説明では強めあう点と弱めあう点を合わせても7つの例しか出しませんでしたが,強めあう点,弱めあう点は他にもたくさんあります。
いま見たように,波が強めあう(弱めあう)には条件を満たす必要があるので,強めあう点,弱めあう点もランダムではなく,規則的に並ぶことになります。 まぁ,見てもらったほうが早いですね。
こんな感じです↓
数学的には「(A,Bを焦点とする)双曲線」と呼ばれる曲線です。
上で導いた,強めあう条件・弱めあう条件が双曲線の定義そのもの(ある2点からの距離の差が一定)になっているので,こういう図形になるのですが,ここで数学の話をしても仕方ないので詳しい説明は他サイトに譲ります。
双曲線の形だけしっかり頭に入れておきましょう!
(上の図ではAとBの間に7本の線を書きましたが,この本数は波長が何mなのか,AとBの距離が何mなのかによって決まります。注意しましょう。)
2つの波源から逆位相の波が出ている場合
最初に出した例題では,A,Bから逆位相の波が出ている場合の干渉条件も求めよ,と言われているので,それもやっておきましょう。
上で求めた強めあいの条件,弱めあいの条件はあくまでも波源A,Bから同位相の波が出ている場合なので,それとはまた違った条件式になるはずです。
さて,A,Bが逆位相なら,片方が山を出しているとき,もう片方の波源は谷を出しているということになります。
よって,波源Aに赤い印を,Bに青い印を重ねます(もちろんAが青でBが赤でもよい)。
この状態から棒を回転させて,強めあう点(同じ色の印が重なる点)と弱めあう点(異なる色の印が重なる点)を探し出します。 そのあとの流れは同じなので,強めあう場合と弱めあう場合を1つずつだけやれば十分でしょう。
◯強めあう場合
◯弱めあう場合
A,Bから逆位相の波が出ているときは,波源からの距離の差が半波長の奇数倍で強めあい,偶数倍で弱めあうということがわかりました。
同位相の場合とは真逆!!
…でもこれって当たり前ですよね?
波源Bと青い印を合わせたということは,さっきまで赤い印があったところが全て青に,青い印があったところが全て赤になったということです。
その結果,さっきは山と山が重なっていた場所が,今は山と谷が重なる点になっています(Pic.2とPic.9を見比べてみよ)。
さっき山と谷が重なっていた場所は,今は山と山(または谷と谷)が重なる点になっています(Pic.5とPic.8を見比べてみよ)。
強めあい・弱めあいの条件は「偶数倍」,「奇数倍」がポイントですが,スタート地点が同位相なのか逆位相なのかで条件が真逆になることに注意してください!
今回のまとめノート
人によっては「あれ?条件式が教科書と違う??」っていう人もいると思うので,ひとつだけ補足。
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
今回は長丁場でした。お疲れ様です。
次回はかの有名な(?)ドップラー効果が登場します。 お楽しみに!!