ドップラー効果という名前と現象は広く知られています。一番わかりやすいのが救急車のサイレン。
救急車が近づいてくるときと通り過ぎたあとでは音の高さがちがって聞こえます(通り過ぎた後はガクッと低くなる)。
ドップラー効果の式を紹介するのは簡単だし,式さえあればある程度問題も解けますが,今回はなぜドップラー効果が起こるのかについて考えてみたいと思います。
【復習】波の用語
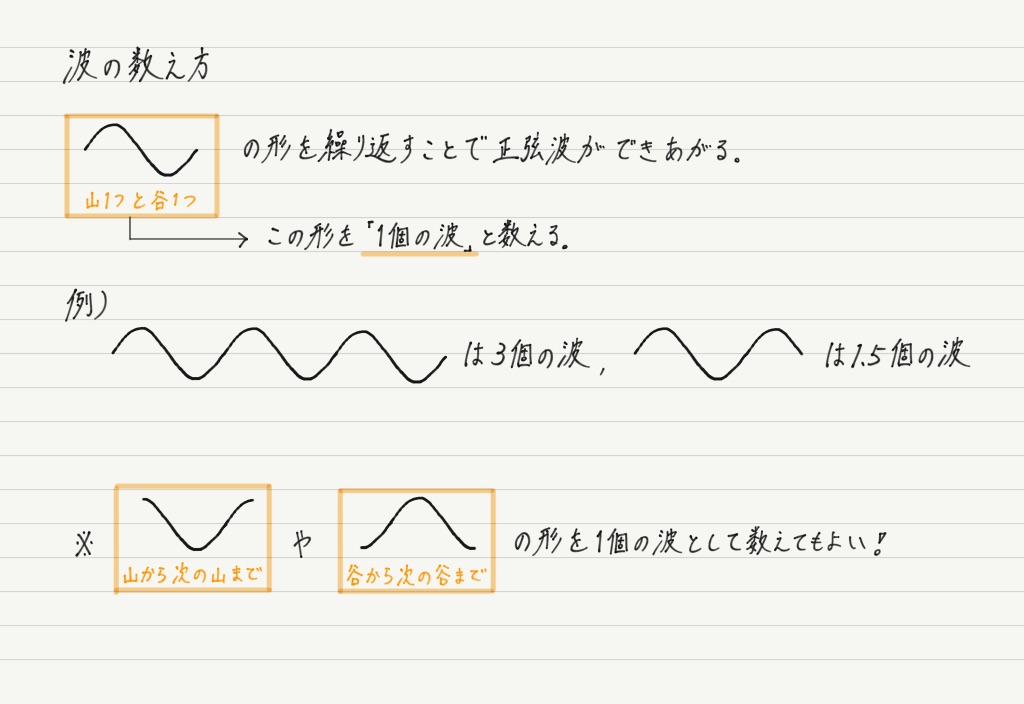
ドップラー効果の原因究明に向けて,波について今一度確認しましょう。 ポイントは「波の数え方」。
「波◯個分」という表現がよく出てくるので,それに慣れてほしいと思います。
物理基礎のときに一度説明しているので,覚えている人は飛ばしてOK!
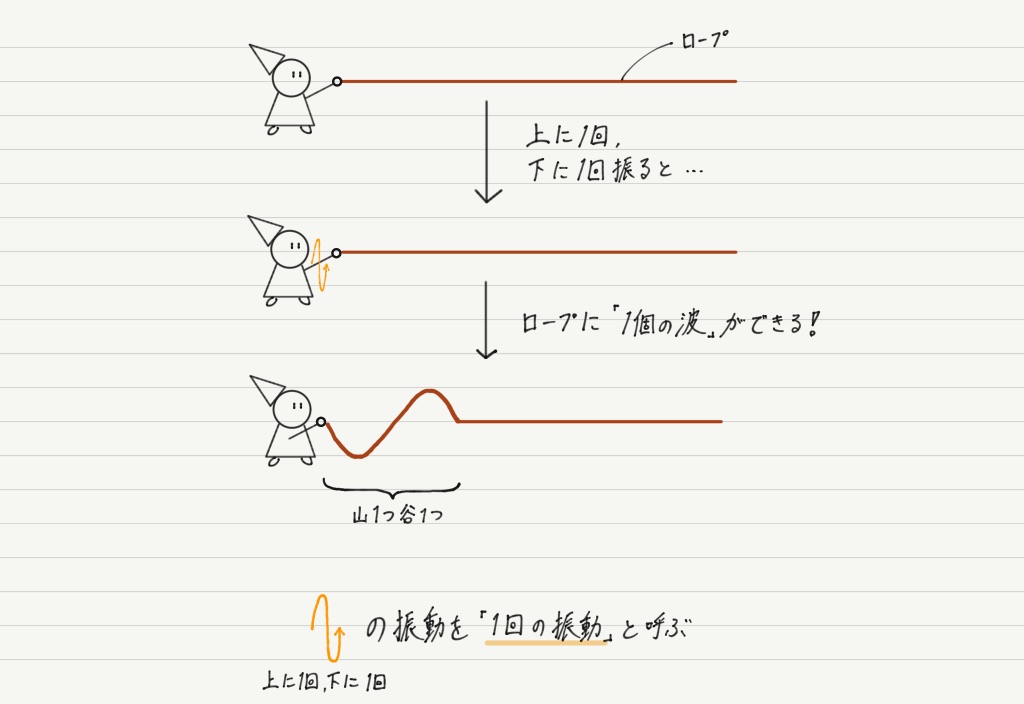
(※ この図は横波の例。音は縦波だが,考え方は横波と変わらない。)
上の図から,媒質を「1回振動」させると,「1個の波」 ができることがわかります。
ついでに振動数についても復習しておきましょう。 波の振動数とは,1秒間に振動する回数のことでした。
以上まとめると,
「振動数f の波」=「1秒間にf 回振動する」=「1秒間にf 個の波ができる」
という解釈ができます。
このように,振動数を「波の個数」として捉えることができると,ドップラー効果の原因の理解にぐっと近づきます!
音速について再考
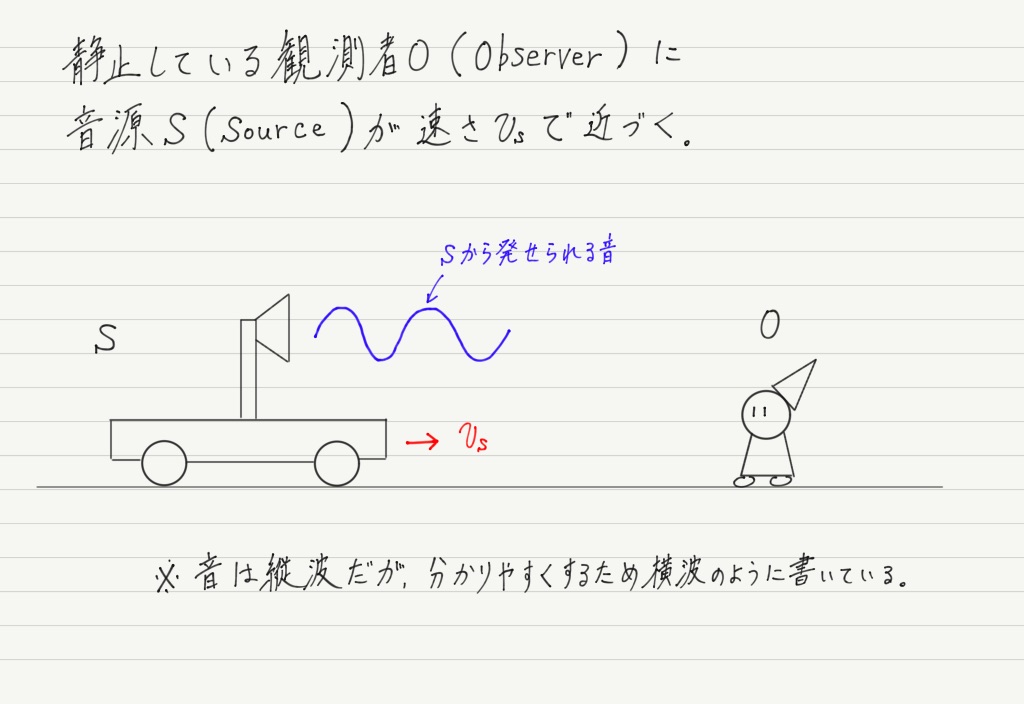
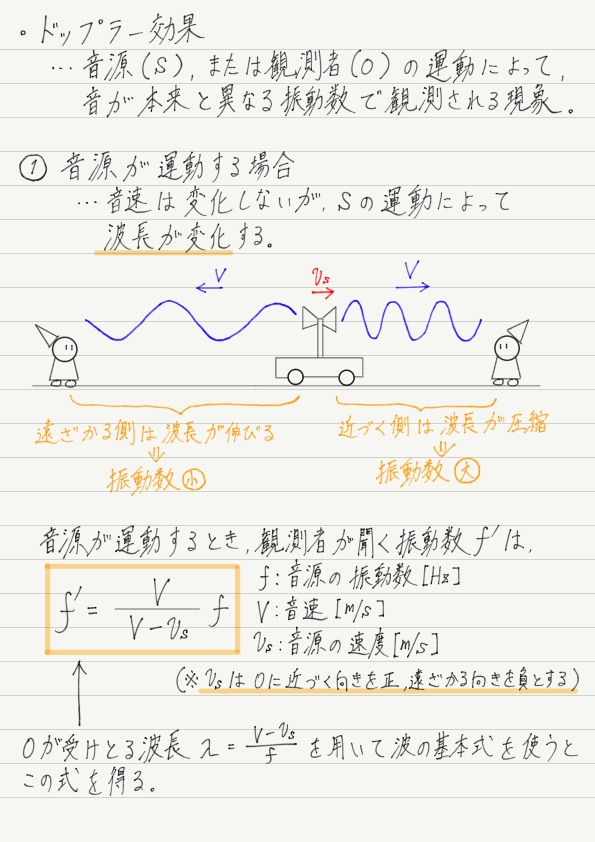
まずは,観測者Oが静止していて,波源Sが近づいてくる場合について考察しましょう。
この場合,観測者が聞く音は実際の音よりも高くなります。
サイレンを鳴らしながら救急車が近づいてくる様子を思い浮かべれば理解できるはず。
このような現象が起こる原因は「発せられた音は音速でしか進まない」ことにあります!!
当たり前じゃん!という声が聞こえてきそうですが…(^_^;)
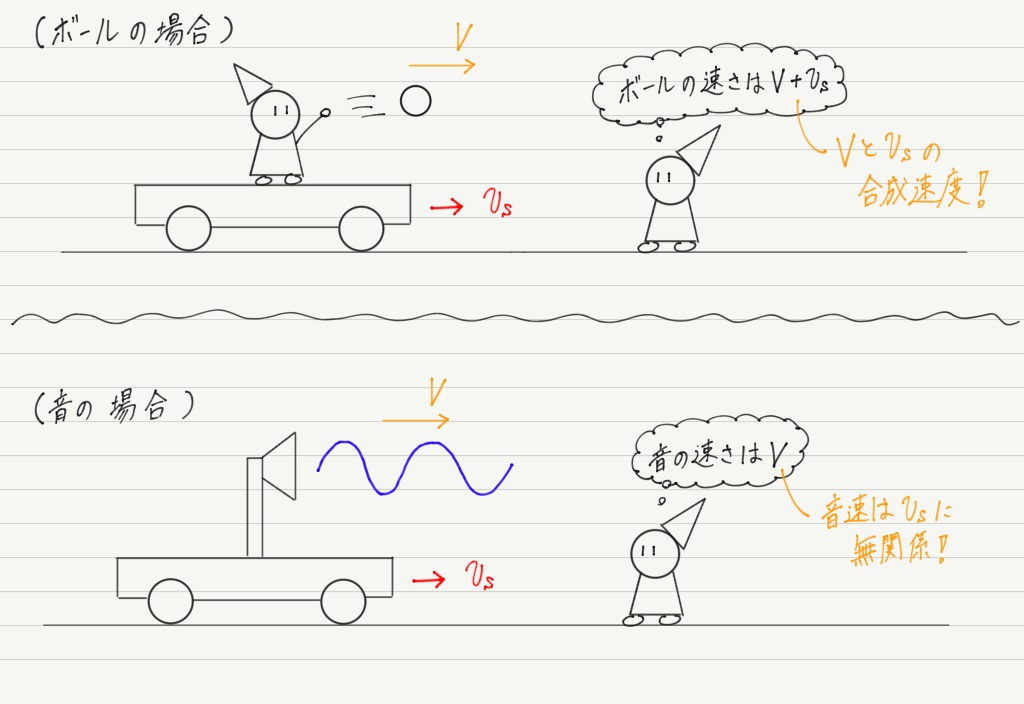
音ではなくボールだったらどうでしょう?
動いている車からボールを投げたら,ボールの速度は車との合成速度になりますが,音の場合はそうではありません。
音速は媒質(と温度)だけで決まってしまうので,車の速度はまったく無関係です!
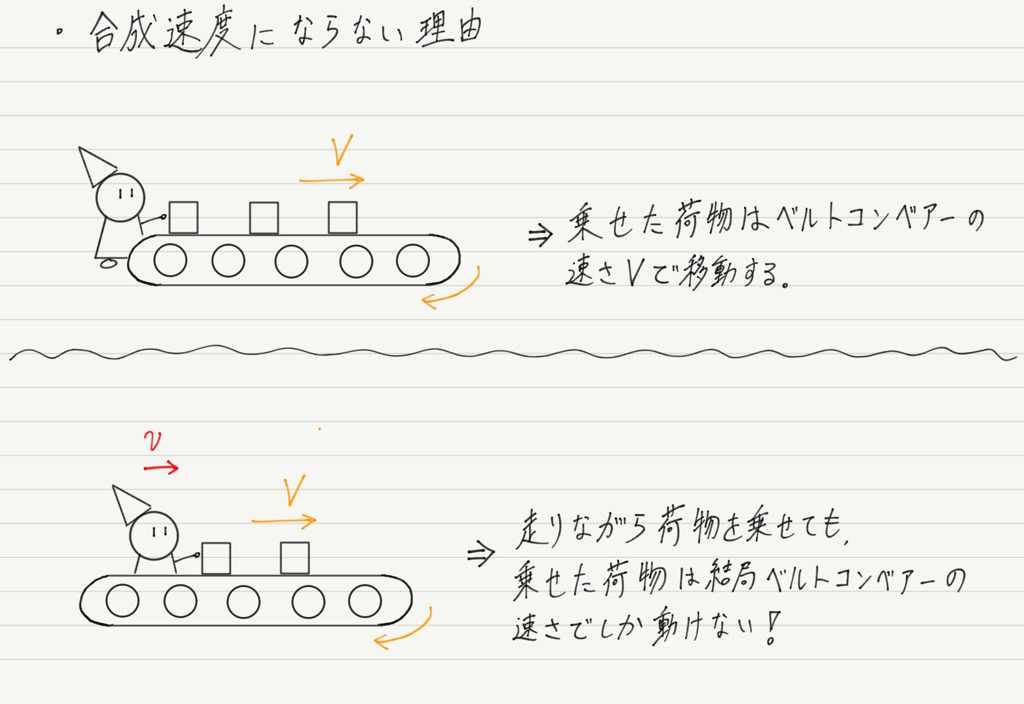
これはベルトコンベアーに荷物を乗せるのに似ています。
ベルトコンベアーに乗せられた荷物は,ベルトコンベアーの速さでしか進めませんよね!
音もこれと同じで,いったん空気中に音が出てしまったら,もう空気中の音速でしか進めないのです。
以上のことを頭に入れた上で,いよいよ考察開始です!
波源が近づいてくる場合の考察
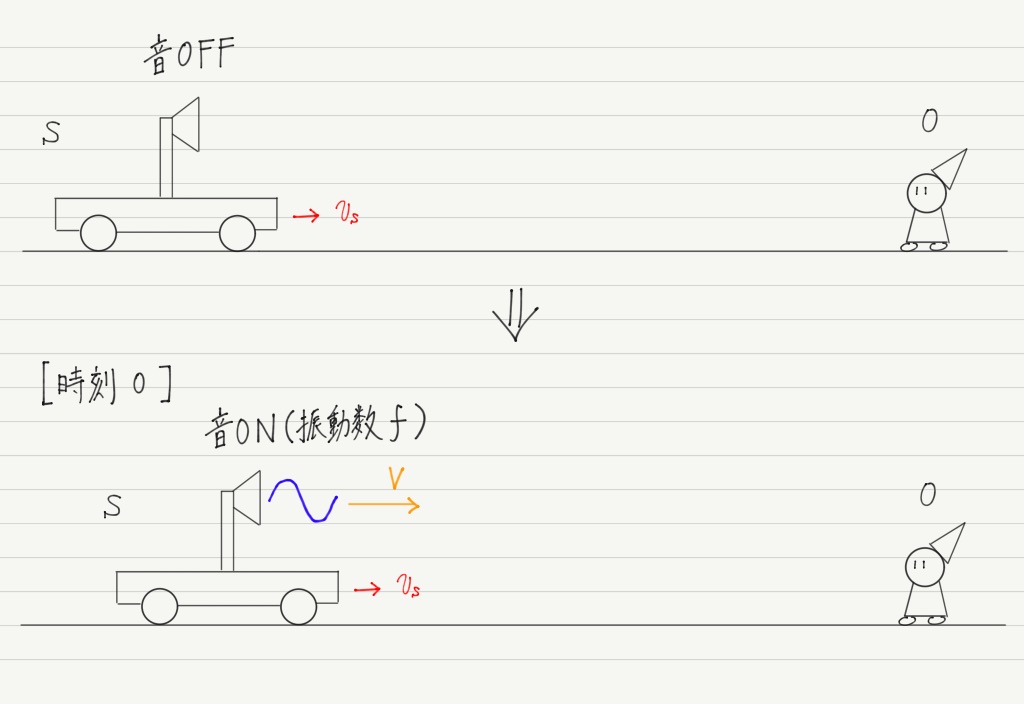
観測者Oに向かって波源Sが等速で近づいてくる様子を想像してください。
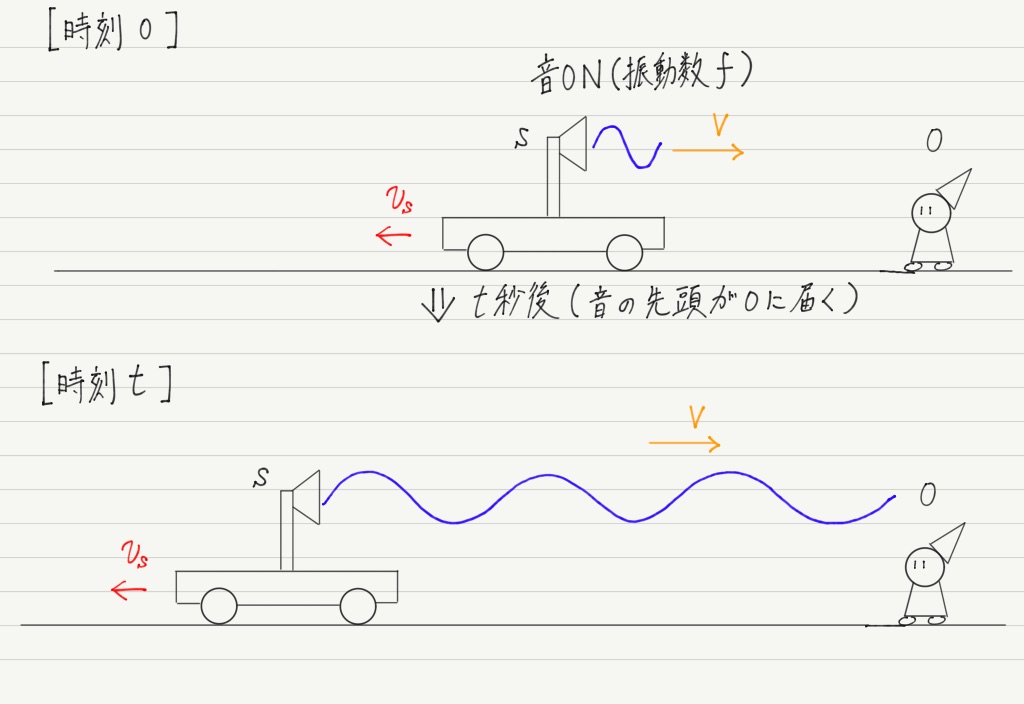
波源Sは最初音を鳴らしておらず,最初に音を鳴らし始めた時刻を0としましょう。
そして,はじめに発した音がOに届く時刻をt[s]とします。 これで考察の準備完了です。
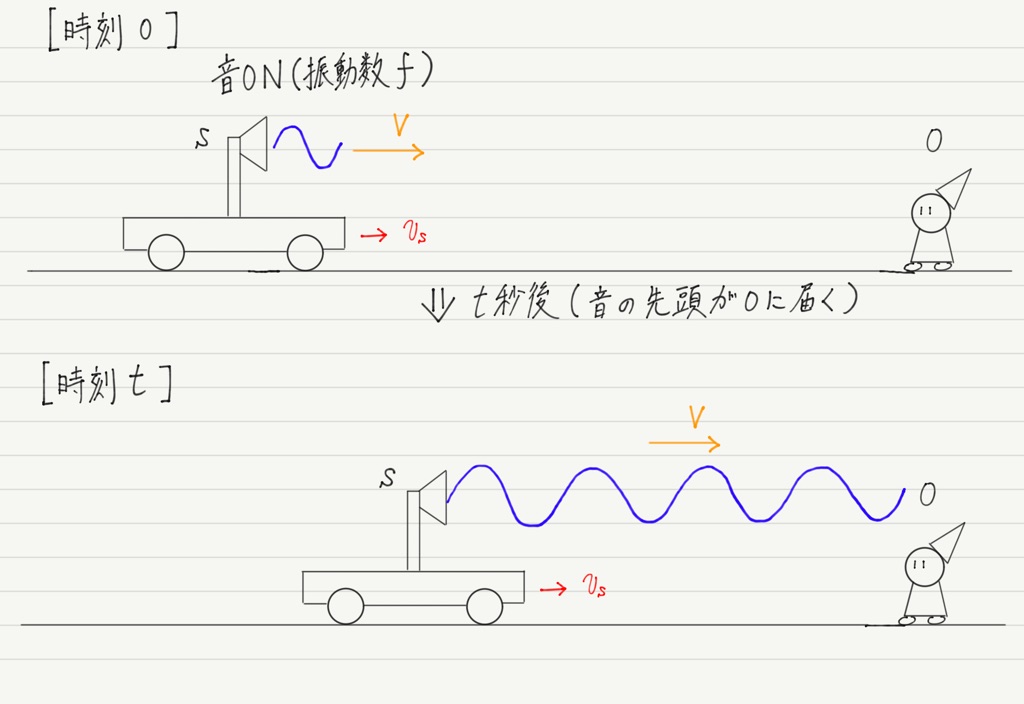
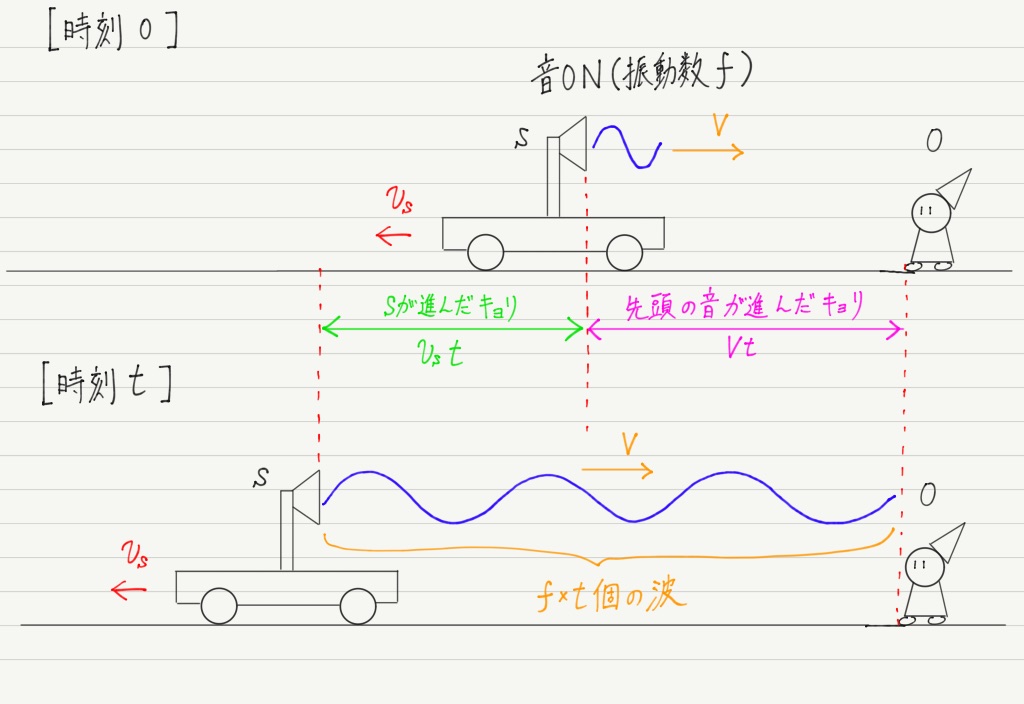
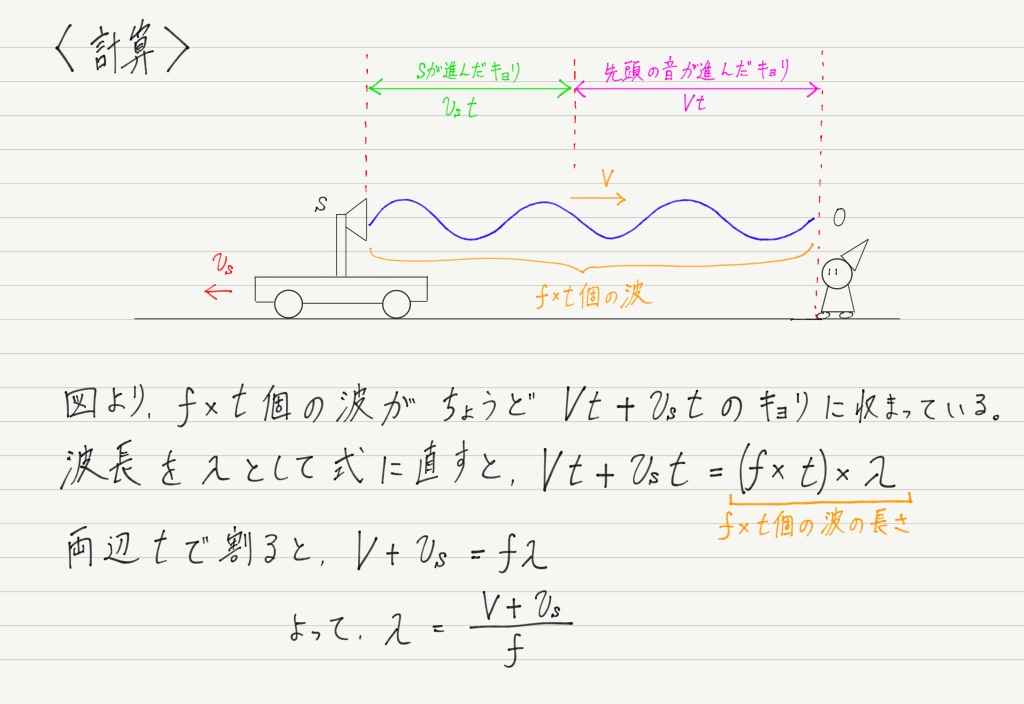
音を発してから最初に観測者が音を耳にするまでにt秒間の時間があるので,この間に波源が出した波は全部で f × t 個です(1秒間にf 個の波を出すからそれをt 倍しただけ)。
問題はその f × t 個の波がどこにあるか。
波の先頭はちょうど観測者に届いたところに,最後の波は波源から出たばっかりなので,波源のすぐ前にあるはずです。
(音速は速いので,波源が音を追い越すことはない)
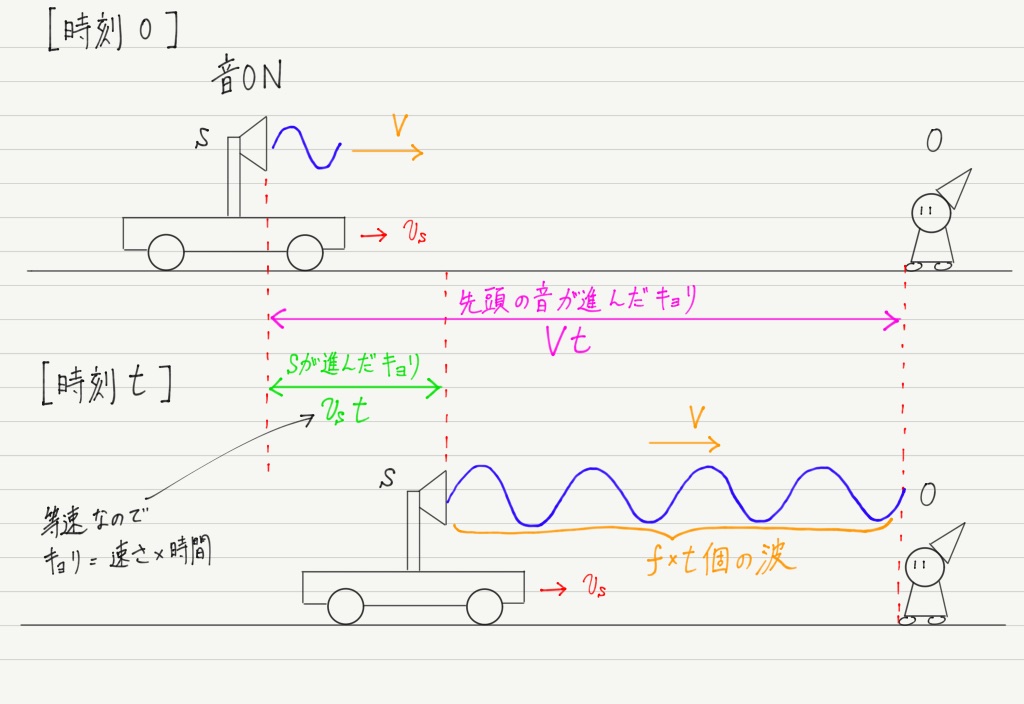
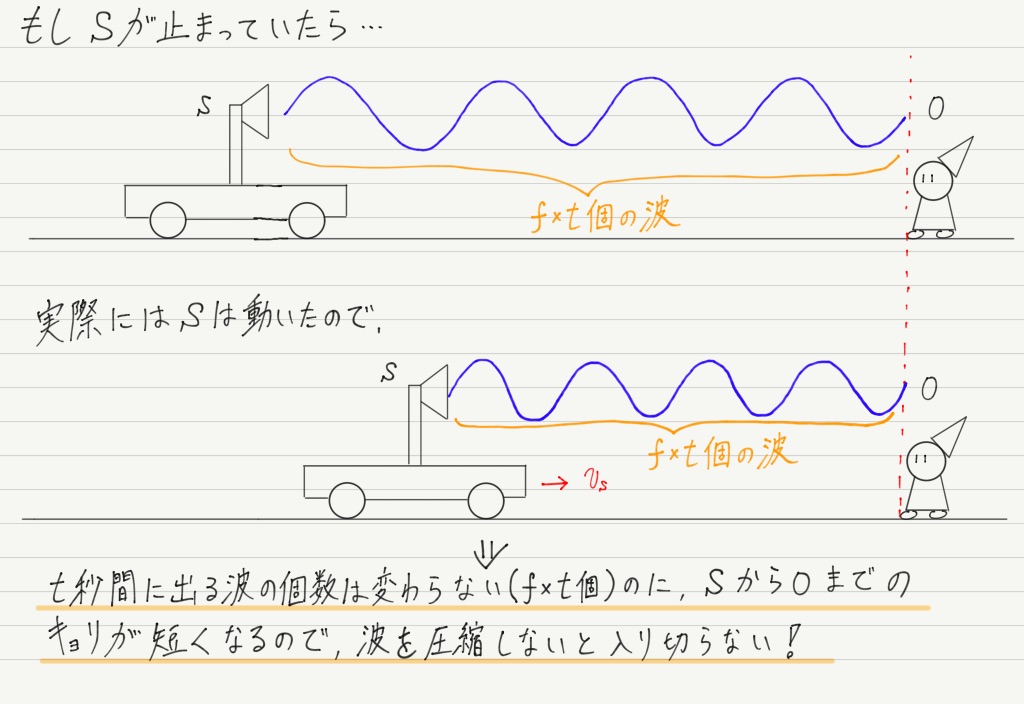
つまり, f × t 個の波は,波源と観測者の間に存在していることになります!
波源が前に進んだ分だけ,波が“圧縮”されているのがイメージできますか?
これが波源が動く場合のドップラー効果の原因なのです!
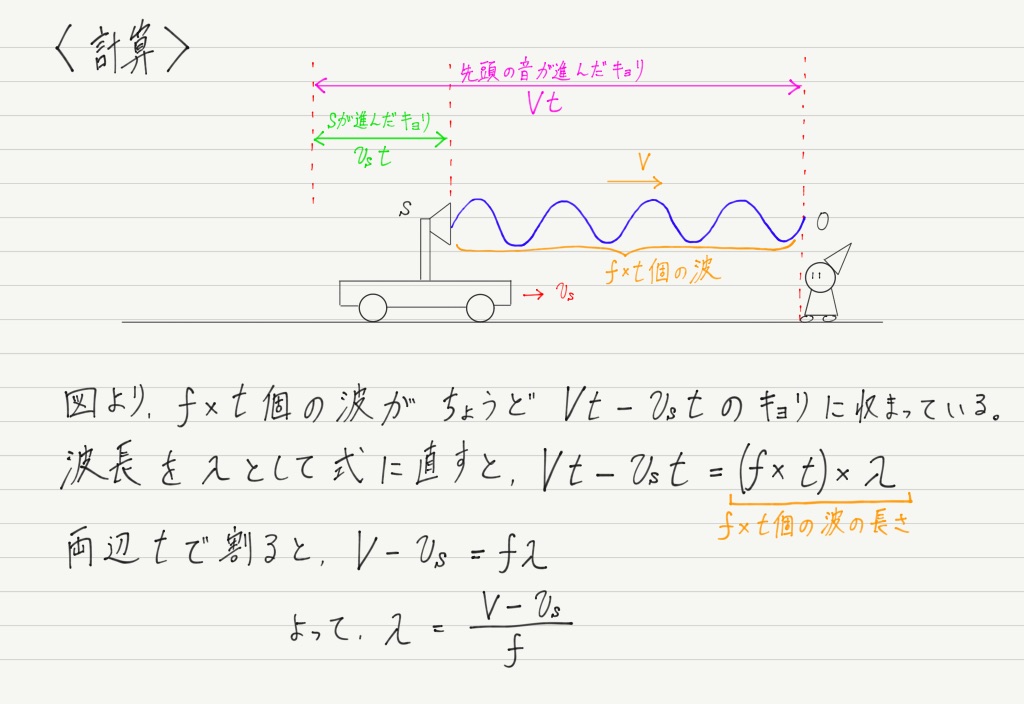
それではこの音の波長λを計算で求めてみましょう。
波長とは波1個分の長さのことなので,計算はこうなります↓
ここまできたら,あとは仕上げ。
音速と波長が分かれば,波の基本式を用いて観測者が聞く音の振動数 f’ が求められますね!
これが音源が近づく場合のドップラー効果の式です!
分母が分子よりも小さくなっているので,f’ がfより大きい(=音が実際より高く聞こえる)ことが式から読み取れます。
波源が遠ざかる場合の考察
逆に波源が観測者から遠ざかる場合も計算してみましょう。 さっきと同じ要領で計算できます。
t 秒間の出来事なので観測者と音源の間に存在する波の個数はやはり f × t 個です。
さっきとちがうところは,波源が観測者から離れていくことによって,波の存在する領域が “引き伸ばされる” 点です(さっきは波源が観測者に近づくので“圧縮”されていた)。
イメージがつかめたところで,観測者が聞く音の振動数 f’ を求めてみましょう。
今度は分母が分子よりも大きくなっているので,f’ がfより小さい(=音が実際より低く聞こえる)ことが式からわかります。
これで,救急車が近づいてくるときは音が高く,通り過ぎた後は音が低くなることが説明できました! めでたしめでたし。
今回のまとめノート
観測者が聞く振動数を求めるだけのような簡単な問題は公式に当てはめるだけで解けますが,少しレベルが上がると,ドップラー効果の根本的な部分が問われます。
そのような問題は「どうやってその公式が出てきたか」を理解していないと手に負えません。
一定以上のレベルを目指す人は,ドップラー効果の式を自力で導き出せるようにしておくことが何より重要です。
問題演習を通じて理解を深めておきましょう!
次回予告
波源ではなく観測者が動く場合でもドップラー効果は起こります。 次回はその点について考察してみましょう!