ここまでの学習で,電場と磁場が荷電粒子にどのような力を及ぼすのかが判明しています。
「力がわかったのだから,運動方程式を使って電場 or 磁場中の荷電粒子の運動を調べてみよう!」という発想にいたるのは当然ですよね?
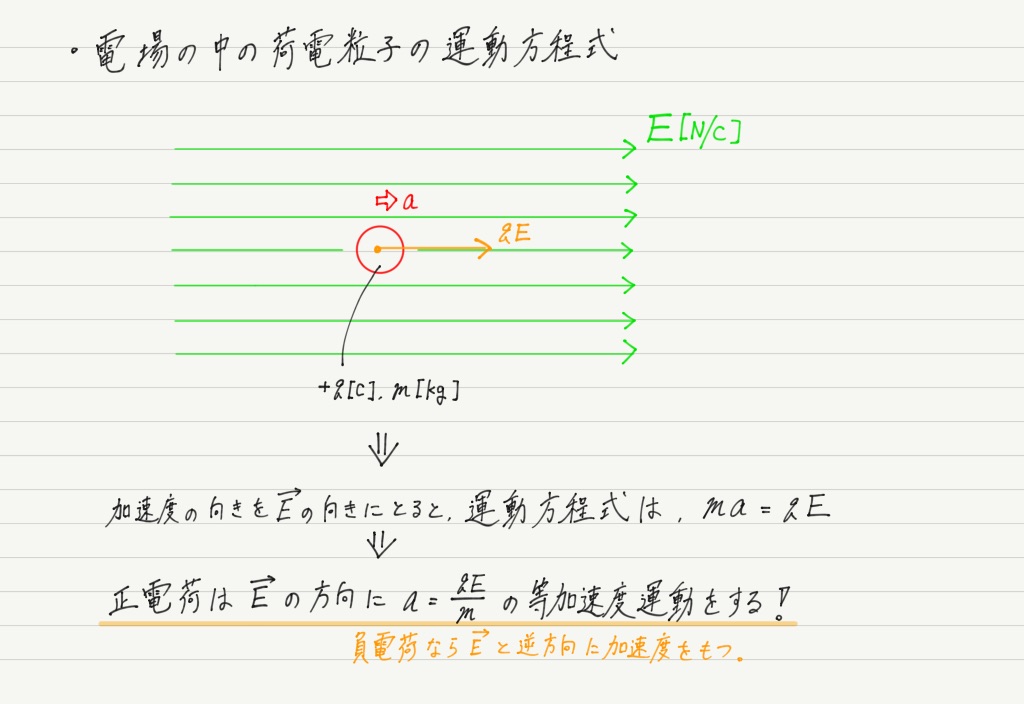
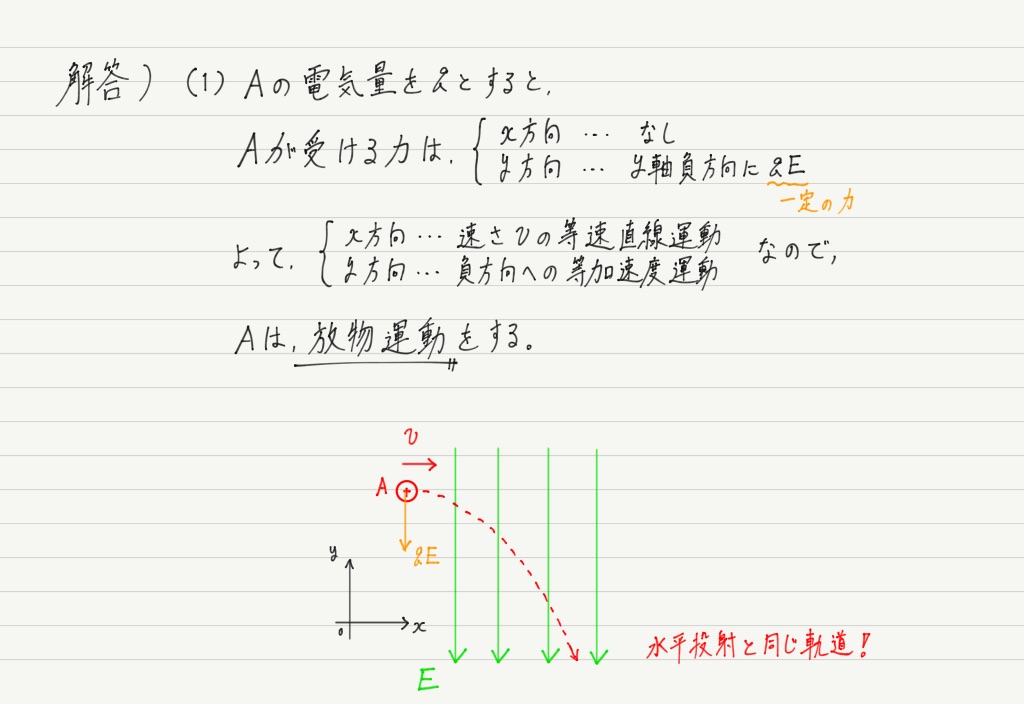
電場の中の荷電粒子の運動
以前学習したように,電場中に置かれた荷電粒子は電場から力を受けます。
その力の大きさは電気量と電場の強さの積,向きは正電荷なら電場と同じ向きで,負電荷なら電場と逆向きでしたね!
では,運動方程式を使って運動を調べてみましょう。
磁場の中の荷電粒子の運動
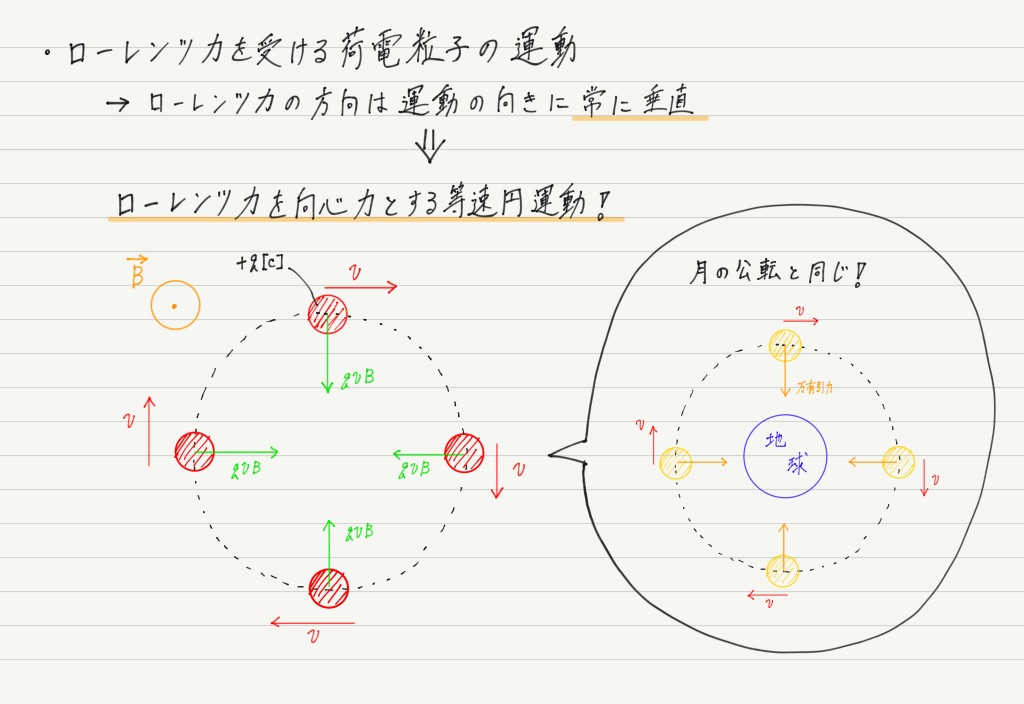
次に磁場です。 磁場の中を運動する荷電粒子はローレンツ力を受けることを前回学びました。
ただし,磁場と平行に運動する場合はローレンツ力は受けないので,今回は磁場に垂直に運動する場合を考えましょう。
さて,「電場のときと同じように運動方程式を立てて…」と,いきたいところですが,
まったく同じようにはいきません。 その原因はローレンツ力の向きに起因します。
ローレンツ力の向きは運動の向きと常に垂直(フレミング左手の法則)でした!
「運動の向きと常に垂直な力」と聞いて,何か思い出しませんか?
… … …
円運動!!
というワードがすぐに出てこなかった人はこれを機に力学を復習しておきましょう。
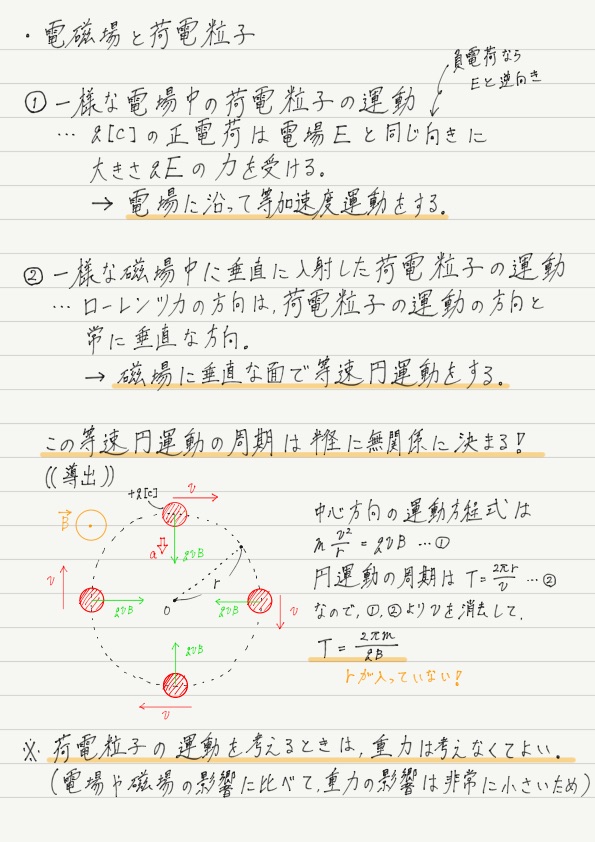
運動の向きに対し,常に垂直な方向に一定の大きさの力がはたらく場合,この力が向心力となって物体は等速円運動をします。
図を描いてイメージをつかんでおきましょう!
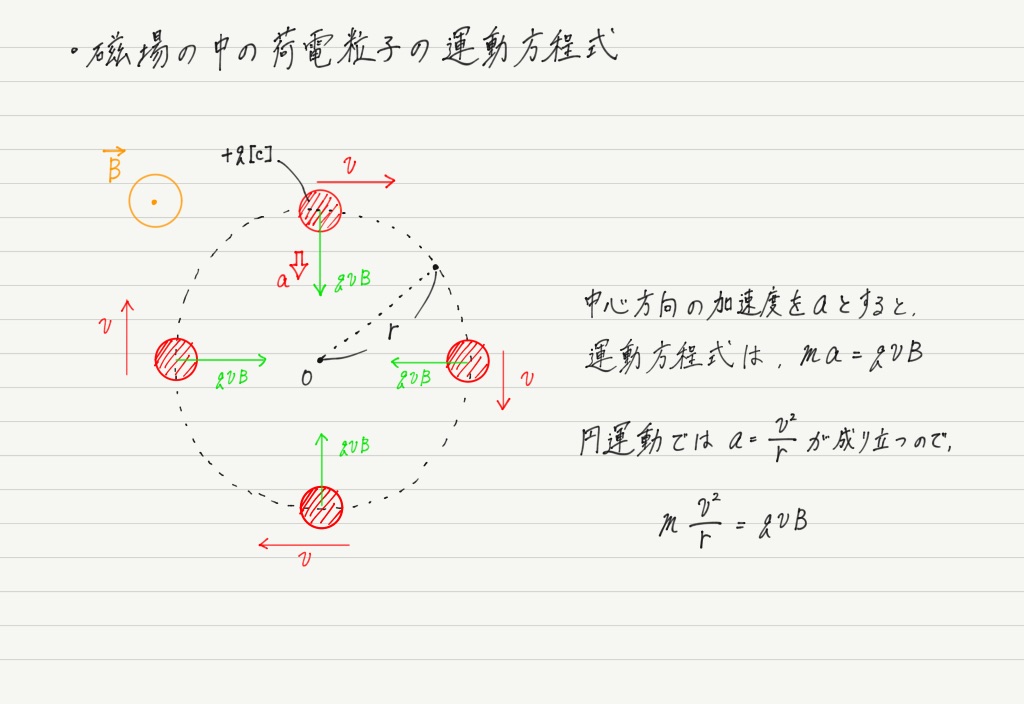
円運動ということは,中心方向の運動方程式を立てればOK。
運動方程式を立てたついでに円運動の周期を求めてみると,ちょっとびっくりする結果が得られます。
…このTの式のどこがびっくりするポイントかわかりますか?
式をもう一度よーく見てください…
連立したときに r が約分されてしまうため,半径を使わずに周期が求められるというのがびっくりポイント!
荷電粒子は円運動の半径が大きくても小さくても,1周するのにかかる時間は同じなのです!!
ふつうは半径が大きくなれば,1周するのにかかる時間もそのぶん増えそうだなーって思いますよね?
直感だけで物事を判断してはいけないという,いい例ではないでしょうか?
粒子の軌道
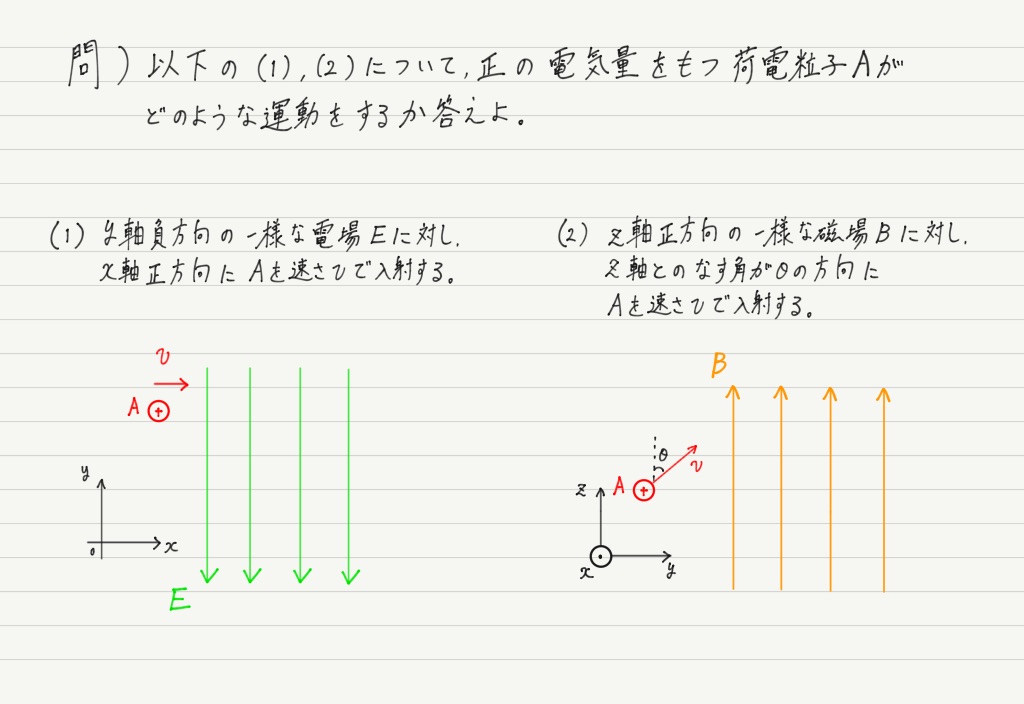
復習を兼ねて例題に挑戦してみましょう。
あ,そういえばさっきから荷電粒子にはたらく重力を完全に無視していますが,重力の大きさは電場や磁場から受ける力に比べて極めて小さいので,電磁場内の荷電粒子の運動を考えるときには重力は無視するのが普通です。
この例題でも重力は無視して構いません。
上で確認したことと,力学の基本的な考え方が身についていれば解けるはずです!
解答はこの下にあります。
では解答。
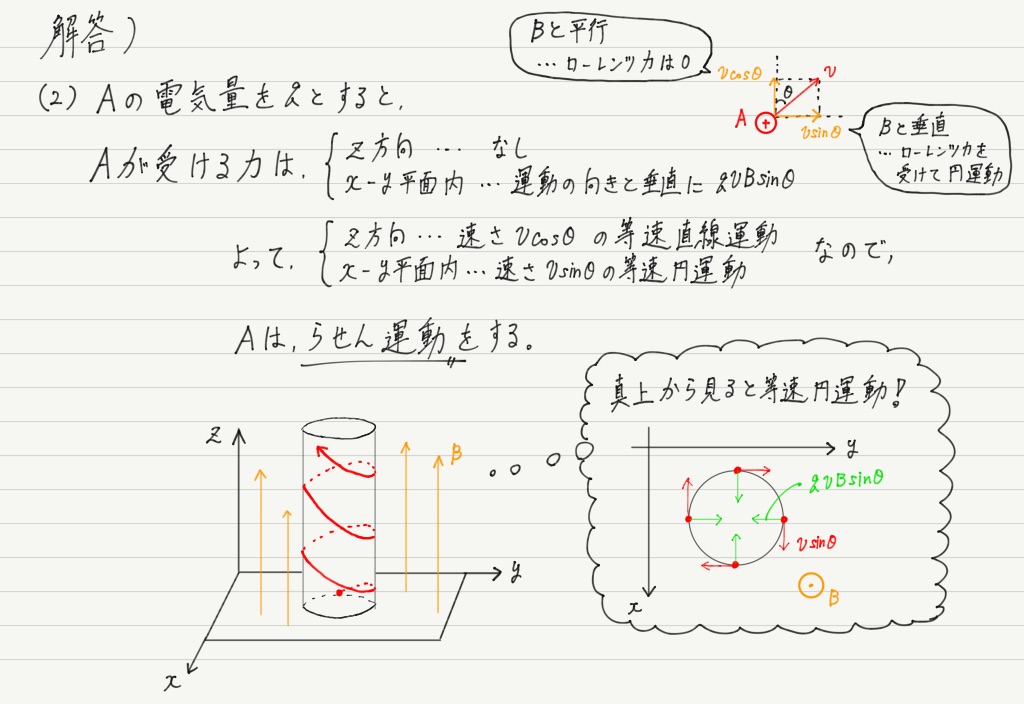
(2)はちょっと難しかったかも?
上の説明では「磁場に垂直に入射する場合」を考えましたが,この問題では斜めに入射させています。
斜め方向こそ,成分に分けて考えましょう!
運動を成分に分けて考えるというのは,力学でやった水平投射(等速直線運動+自由落下)や,斜方投射(等速直線運動+鉛直投げ上げ)とまったく同じ発想!
まぁ,等速直線運動+等速円運動=らせん運動っていうのは答えにくかったかもしれませんが…
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
いよいよ電磁気の山場である電磁誘導に突入します!