力がはたらかなければ等速直線運動,一定の力がはたらけば等加速度運動,というように,
それぞれの運動には “その運動をする理由” があります。
円運動の場合,それはどんな理由なのでしょうか?
リンゴも落ちるが月も落ちる?
円運動の条件を書くのは簡単ですが,それでは味気ないので歴史的な経緯に触れましょう。
(※ わかりやすさを重視したので,正確な史実だけでなくフィクションも含まれます)
昔々,人類は「自分たちのいる地上」と「神がいる宇宙」を分けて考えていました。
地上と宇宙が別物であるという例のひとつが物体の運動です。
地上で物体を自然に落下させると真っ直ぐ落ちる → 地上の運動は直線運動が基本。
天体は地球の周りをまわっている(ように見える)→ 宇宙の運動は円運動が基本。
という感じで,「やっぱり宇宙は特別なんだ」と思っていたようです。
…やがて時が経ち,アイザック・ニュートンによって,この考えは覆されることになります。
ニュートンといえばリンゴが落ちるのを見て重力を発見したという伝説が有名ですが,実はそうではありません。
おそらく重力の存在はすでに知っていたはずで,彼が考えていたのは別のこと。
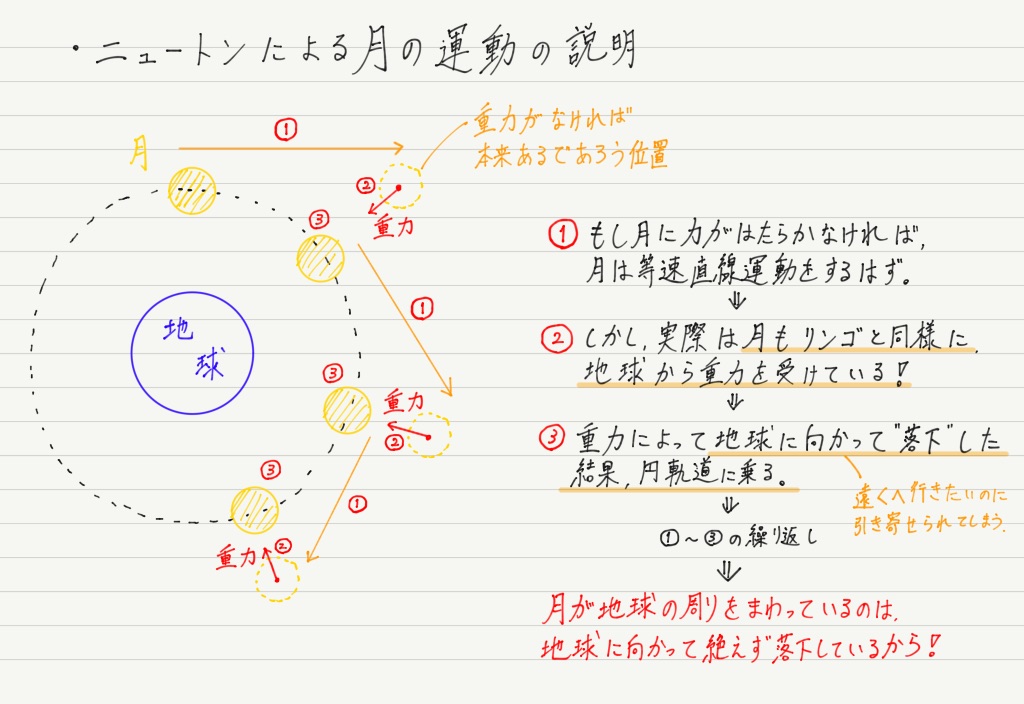
それは,「なぜリンゴは落ちるのに月は落ちてこないのか?」という問い。
考えた末,ニュートンはある真理に到達します!
やはり月も落ちているのだ,と。
ちょっと何言ってるかわからないと思うので,説明しましょう。
(※ 上の図は誇張して書いています。① → ② → ③の順で起こるというより,①,②,③はほぼ同時に起こると考えてください。)
ニュートンが言いたかったのは,「月の円運動は落下した結果。リンゴも月も重力を受けて落下する。つまり,地上でも宇宙でも物理法則は同じである。」ということなのです。
円運動と向心力
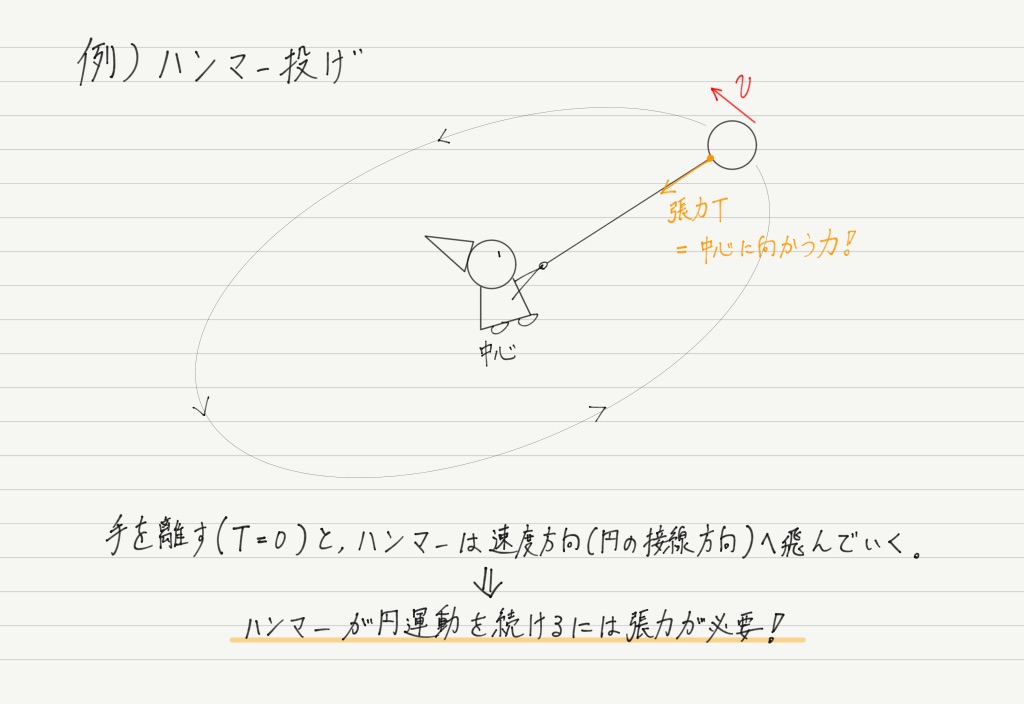
ニュートンの考えが正しいとすると,中心に向かってはたらく力が存在すれば,月以外のどんな物体でも円運動をするはずです。
この例を見れば,「中心方向の力があれば物体は円運動をする」というだけでなく,
「円運動するためには,必ず中心方向へ向かう力が必要」ということもわかります。
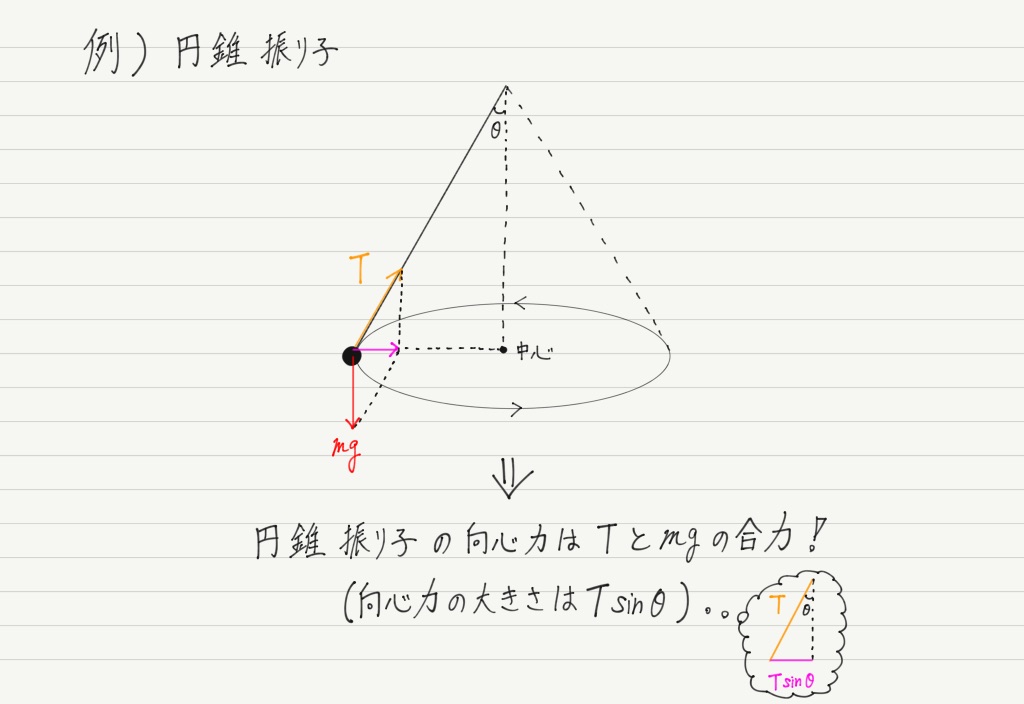
円運動において,中心方向へ向かう力のことを向心力といいます。
なお,向心力(中心方向)と速度(円の接線方向)は常に垂直な関係を保っていることに注意してください。
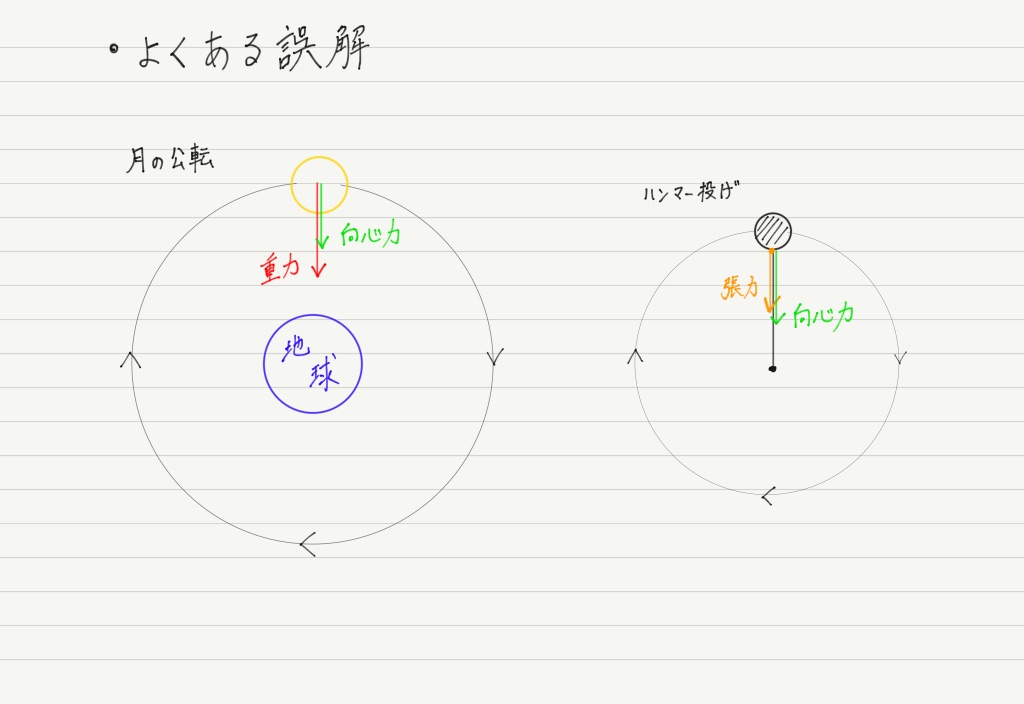
向心力に関するよくある誤解
教科書を見ると,「円運動する物体は向心力を受けている」というような文が書かれていますが,この文のせいで向心力を勘違いする人が続出しているので要注意!
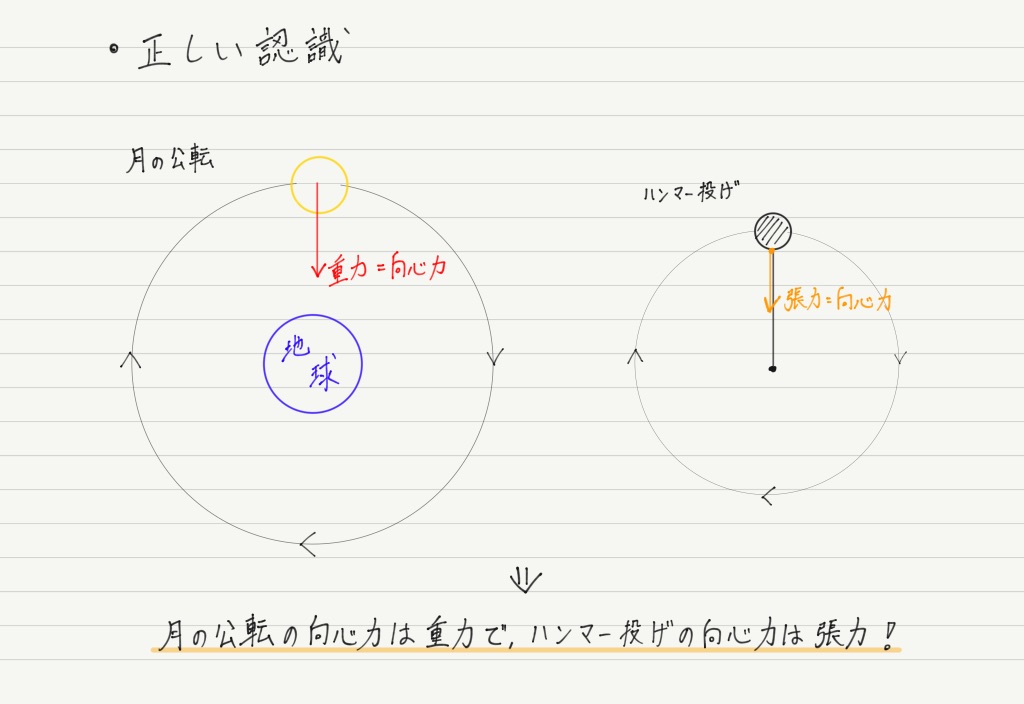
よくある誤解と正しい認識を具体的に記しておくので,よく見てください!
要するに,「円運動している物体には,向心力という新たな力が出現する」というのがよくある誤解で,「物体にもともとはたらいていた力のうち,中心方向を向いているものを向心力と呼ぶ」というのが正解です!
誤解したままだと問題がまったく解けなくなるので,正確に理解してください。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は円運動を具体的に調べていきます。
直線だろうが円だろうが,運動を調べるといえば使うのはもちろんアレですよね!