「保存力」というワードを覚えていますか？ 前回学習した静電気力は，実は保存力の一種。 保存力の性質でもっとも重要なのは，保存力ならば位置エネルギーを計算することができるという点です！！
↑の記事の中で予告した通り，静電気力による位置エネルギーが今回いよいよ登場します！
重力との比較
「位置エネルギーが存在する」なんてサラッと言っちゃいましたが，重力による位置エネルギーの場合と比較すると，位置エネルギーの存在が納得できると思います。
（※ここでは，電場の大きさEはどこでも一定と仮定しています。）
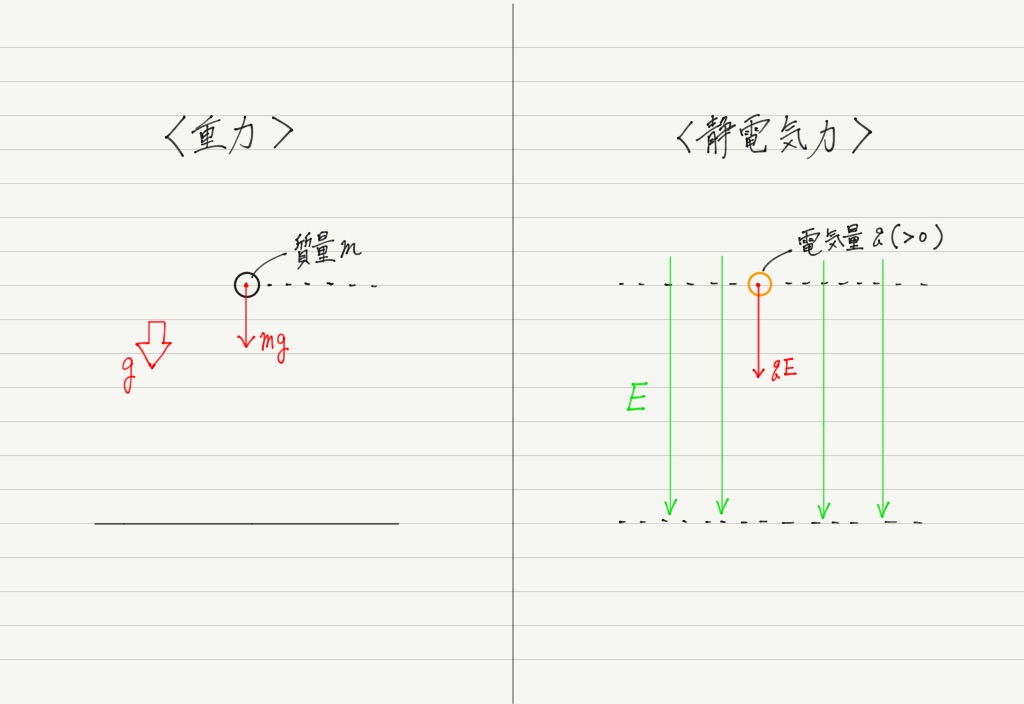
ね？ 質量mの物体が重力に沿って落ちていくのと，電気量qの点電荷が電場に沿って「落ちて」いく様子は図にしてみるとそっくりです（※以前の記事ではF＝qEのqに絶対値をつけていましたが，今回は電荷の符号のちがいも含めて考えたいので，絶対値を外しています）。
現象がそっくりということは，その背後にある物理法則もそっくりのはず。
通常の物体が，位置エネルギーを運動エネルギーに変えながら落ちていくのなら，電荷だって位置エネルギーを運動エネルギーに変えながら「落ちて」いくはずです。
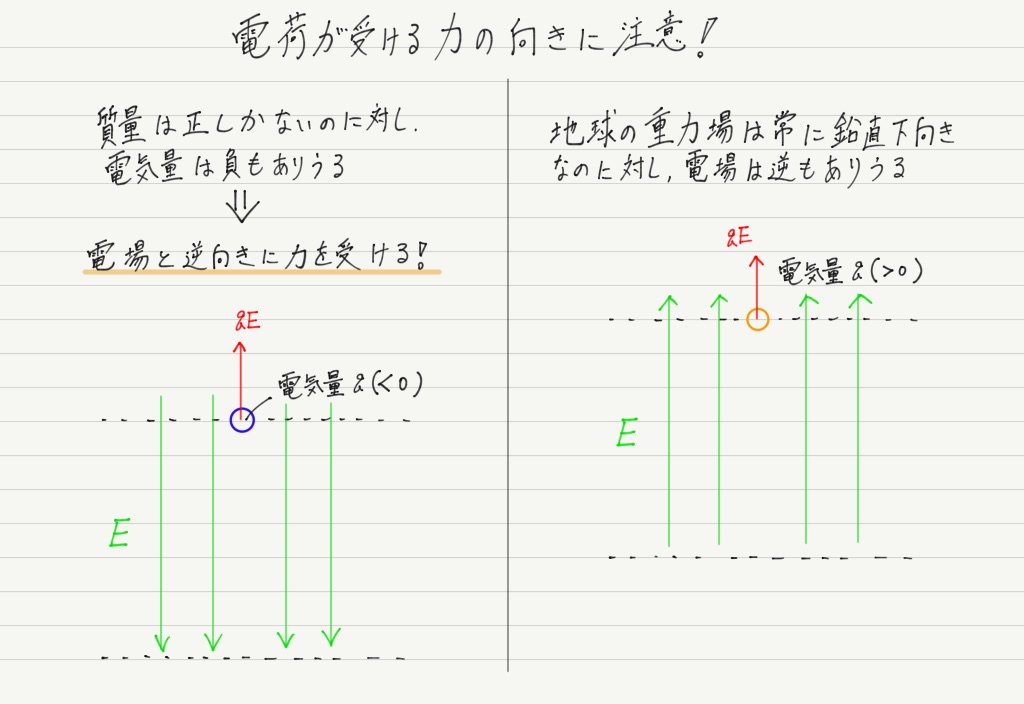
重力による運動と静電気力による運動。 このようにたしかに似ていますが，一箇所だけちがう点があります。 それは，物体は鉛直下向きにしか落ちないが，点電荷は電場の向きや電気量の符号によって，受ける力の向きが変わるという点です。
つまり，場合によっては「上向きに落ちる」こともあるわけで（落ちるという表現が正しいかは置いといて），そこが重力との決定的な差です。
2つのモノを比較するときは，似ている点と異なる点の両方をしっかり意識しましょう！
位置エネルギーを求めるには
静電気力にも位置エネルギーが存在するということがわかったので，次に問題になるのはその計算方法です。
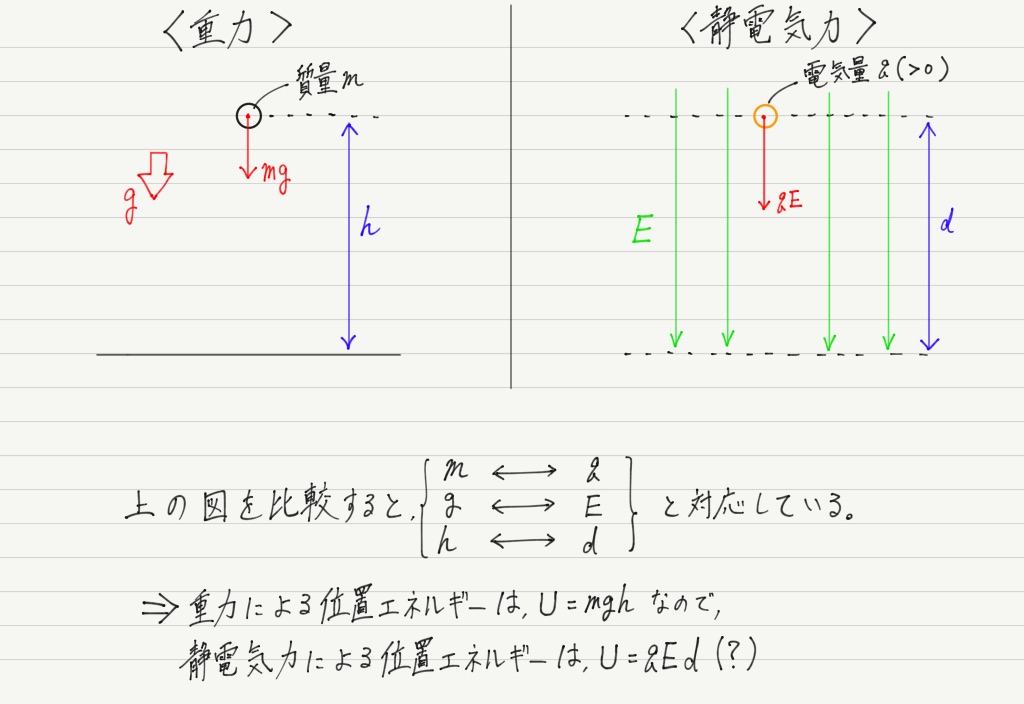
重力による位置エネルギーの場合はmgh，つまり，質量m，重力加速度g，高さhを用いて計算しましたが，静電気の位置エネルギーもまずは同じように考えてみましょう。
m，g，hに対応している文字をそのまま当てはめただけですが，結論から言うとこの式は正しいです。 しかし，注意すべきはこの式の見方。 重力による位置エネルギーの式mghは，m×g×hと見るのではなく，mg × hと見るのが正解。
もともと「エネルギー＝仕事」なので，重力mg × 距離hというわけです。 静電気力による位置エネルギーも同様に，静電気力qE × 距離dと考えられます。
…同じじゃねぇか！って？ いえ，ここからが大事。 実は静電気力による位置エネルギーには，もう1つの解釈があります！
それは，q × Edという見方です。
重力で同じ見方をしようとすると，m × ghなってしまって，「ghって何？？」って感じなのですが，電気の世界ではEdはとても重要な意味をもっていて，「電位」と呼ばれています。
電位は記号Vで表すことが多く，この記号を用いると，V＝Edとなります。
よって，位置エネルギーの式をVを用いて書き換えると，U＝qVとなります。
この式を見て分かるとおり，静電気力による位置エネルギーUは，電位が一定ならば電気量qに比例します！
また，q = 1Cを代入するとU = Vとなるため，「電位 ＝ 電荷1Cあたりの位置エネルギー」と解釈可能。
静電気力による位置エネルギーは「力 × 距離」と「電位Vを求めて，それをq倍する」という2通りの解釈が可能ということになります！
静電気力のする仕事
エネルギーが求められるようになったので，仕事も計算することができるようになりました！！
この仕事の式を少し変形させてみると…
さっき電位という言葉が出てきたとき，「電位差」というワードを思い浮かべた人が多いのではないでしょうか？ 電位差とは電圧の別名でしたね！
物理基礎では「電圧とは，電気の世界における高さ」と表現しましたが，なぜ「電圧＝高さ」なのか，ここでようやくその根拠が示されたことになります。
このイメージはこれから先（特に回路の問題）も大事にしてほしいと思います。
なぜ電位という概念を持ち出すのか
話は少し戻りますが，力学ではghに何の意味もないのに，電気ではEdにわざわざ「電位」という名前までつけて意味づけしているのはなぜでしょう？
それは，電位が直接測定できる量だからです。 力学でもしghを求めようと思ったら，まず高さhを測定して，その後gをかけ算して求めることになります。
ところが電気の場合，たとえば電気回路なら，電圧計を用いればEとdが分からなくても，電位Vを直接求めることができます。
つまり，仮に力学でghに何か名前をつけて記号を与えたとしても，位置エネルギーを求めようと思ったら，結局mとgとhをそれぞれ求めなければいけません。
一方，電気では必ずしもqとEとdを求める必要はなく，qとVでも求められる。 これが力学と電気の大きなちがいであり，わざわざEdに「電位」と名付けている理由でもあります。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
静電エネルギーという用語は，物理では別の意味で用いられます（いずれやります）。
次回予告
電位が分かれば位置エネルギーが求められるということなので，次回は電位の求め方を扱っていこうと思います。
