「電位＝1Cの電荷がもつ静電気力による位置エネルギー」だったので，電位が分かれば，静電気力による位置エネルギーを簡単に求められることになります。
と，いうわけで，今回は電位の求め方を学んでいきましょう！
点電荷のつくる電位を求める
空間中に点電荷が置かれると，そのまわりには電場が生じるのでした。 その電場の大きさは計算で求めることが可能です！
電場だけでなく，点電荷のまわりの電位も計算できるので，伝授しましょう！！
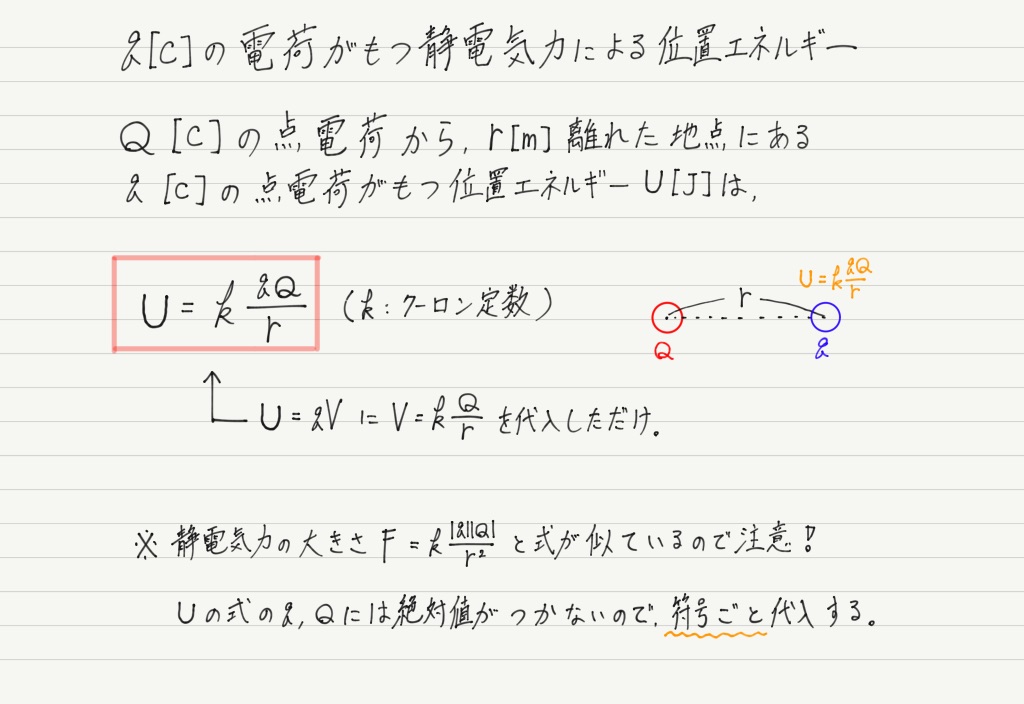
これを用いれば，電場の中に置かれた q［C］の電荷がもつ位置エネルギーも求めることができます。 電荷1Cあたりの位置エネルギーがVなので，q［C］の電荷なら，Vをq倍すればOKですね！
ところで，位置エネルギーといえば基準が大事になってきますが，今回のような2つの点電荷の間で位置エネルギーを考えるときは，無限遠を基準にとるのが一般的です。 なぜそんな変なところを基準にとるのかって？
その理由は，基準では位置エネルギーは0となるようにしたいからです！
もちろん同じ理由で，点電荷による電位Vの基準も無限遠になります。 無限と言われるとイメージしづらいですが，「無限遠でU = 0（V = 0）」だけ覚えておけば計算で困ることはありませんので，安心してください。
（万有引力による位置エネルギーのところでも同じような話をしているので，未読の方はこちらもぜひ。）
これで式の紹介はおしまい。 あとは例題をやりながらいくつか補足していきます。
例題① 複数の電荷がつくる電位
あれ… この問題どこかで見たような？ 細かいことは気にせず（笑），まずは上の公式を使って解いてみてください！
（3）のヒント。 電荷が複数ある場合，ある地点での電位は，それぞれの電荷がその地点につくる電位を足し合わせたもの（電位の重ねあわせ）になります。
解答です↓
さて，気づいた人もいると思いますが，この問題は電場のところで扱った問題をそのまま流用しました。 手抜きをしたいわけではなく，電場と電位のちがいを認識してほしかったからです。
電場＝（1Cあたりの）静電気 “力” なので，向きがあるベクトル量，
電位＝（1Cあたりの）位置 “エネルギー” なので，向きがないスカラー量。
ベクトルは向きを考えて足す必要がありますが，スカラーはただ数値を足すだけでOK。
力学で運動エネルギーと位置エネルギーを足して力学的エネルギーを求めるとき，向きなんて考えませんでしたよね？
（※ 電位の値が負になることもあるが，それは「逆向き」のマイナスではなく，「0（基準）より小さい」という意味でのマイナス）
電場を求める問題と，電位を求める問題 。 よく似ていますが，しっかり区別しておきましょう！
例題② 力学的エネルギー保存の法則
電位Vから静電気力による位置エネルギーUが求められるようになったので，エネルギーを用いた計算も可能になりました！ 使うのはもちろん力学的エネルギー保存の法則。
位置エネルギーが重力によるものでも，ばねによるものでも，静電気力によるものでも，運動エネルギーと足し合わせれば，それは力学的エネルギーになります。 問題の解答はこの下にあります。
解答です。
このように，力学的エネルギーが保存するという考え方は電気の世界でも活きてきます（力学的エネルギーが保存する条件には注意すること！）。 適用範囲の広さこそ物理最大の武器！！
解答にも書き込みましたが，点電荷の問題で力学的エネルギーを用いる場合，重力による位置エネルギーは考えない（質量が非常に小さいので影響が無視できる）のが普通ですので，自分で問題を解く際にも気をつけてください。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
今回例題のところで，電場と電位のちがいが登場しました。 両者はもちろん異なるものですが，密接に関係しているのもまた事実。 次回はその辺りに焦点をあててみましょう！
