前回の講義では触れませんでしたが，万有引力は保存力の一種です。 ここで，「保存力には必ず位置エネルギーが付随する」ことを思い出しましょう。
このことから，重力による位置エネルギーや弾性力による位置エネルギーのように，「万有引力による位置エネルギー」も存在することが導かれます！
いったいどのようなエネルギーなのか，詳しく見ていくことにしましょう。
万有引力による位置エネルギーの式
では早速ですが，万有引力による位置エネルギーを求める公式を伝授しましょう。
どこからこの式が出てきたのかはさておき，まずはこの式をちゃんと覚えてください。
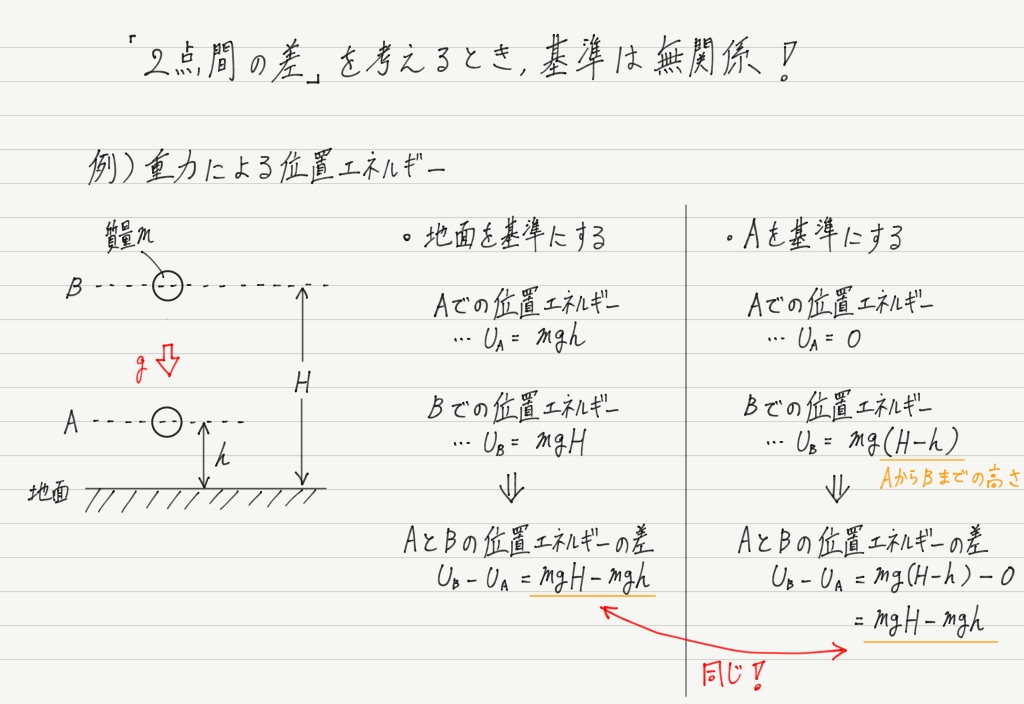
それから，位置エネルギーにおいては「どこを基準にするか」が重要です。 大事なのは，物体が基準にあるとき，位置エネルギーが0であること。 これを踏まえた上で，基準を探ってみましょう！
無限に遠い地点が基準…？
不自然な感じがするのは否めませんが，位置エネルギーが0になる地点がそこしかないので諦めましょう笑
そもそも位置エネルギーというものは，2点間の差を考えたときにはじめて意味をなす概念なので，基準はどこにとっても変わりません。
「どこにとっても変わらないなら適当でいいじゃん？」ではなく，「どこにとっても変わらないなら計算しやすい基準のほうがよくね？」と考えた結果が，基準＝無限遠なのです。
位置エネルギーにマイナスがつく理由
公式を紹介した時点で今回の内容は終わったと言ってもいいのですが，多くの人が引っかかるポイントについて補足しておきます。
「なんで万有引力による位置エネルギーの式にマイナスがついてるの？？」ってやつです。
教科書や参考書ではご丁寧に仕事の概念を持ち出して説明していますが，その説明でわかるレベルの人はそもそも疑問に思っていないんじゃないかっていう(^_^;)
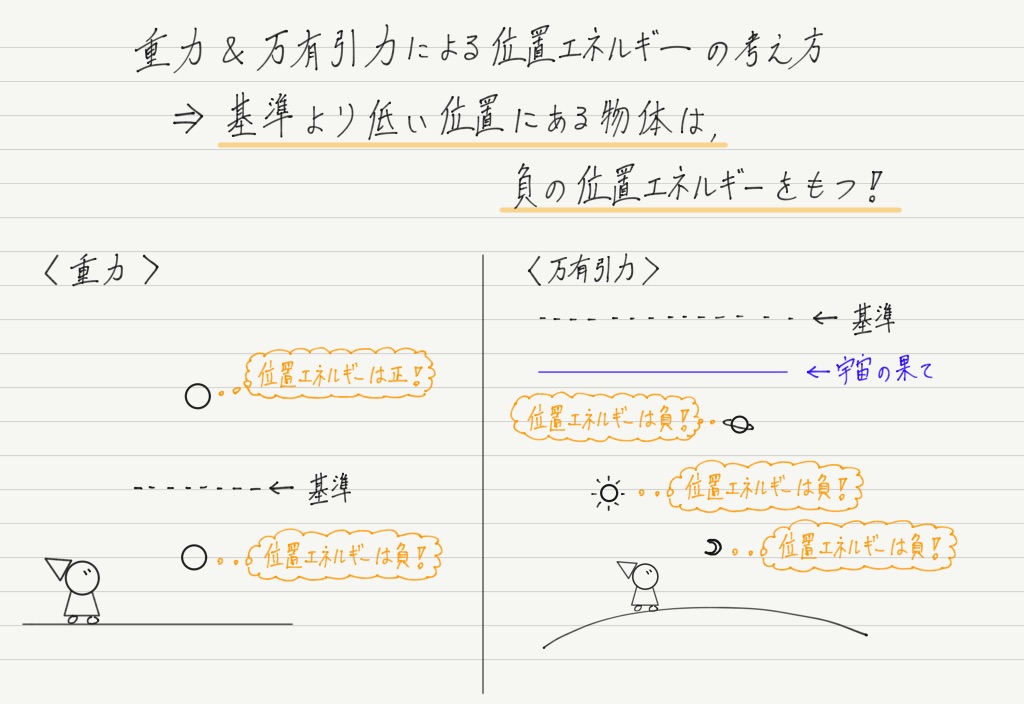
この疑問に対する私の答えはズバリ，「基準より下にあるから」
前回の講義で，「地球の万有引力と重力はほぼ同じもの」という説明をしましたが，だったら位置エネルギーの考え方も共通してるはずです。 思い出してほしいのは，重力による位置エネルギーでは，基準より下にある物体がもつ位置エネルギーが負の値をとるということ。
万有引力の位置エネルギーの場合，基準は無限の彼方なので，地球上にいる我々から見たとき，この世のすべての物体は基準より低い位置にあることになります！！
位置エネルギーの基準に対して物体がどこにあるのか，ただそれだけの話なのです。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
長きに渡った力学も，いよいよ最終講を迎えます。 最後は万有引力が関係する運動の問題に挑戦しましょう！
