電場と電位。似た用語ですが,全く別物。
前者はベクトル量,後者はスカラー量ということで,計算上の注意点を前回お話しましたが,今回は電場と電位がお互いにどう関係しているのかについて学んでいきましょう。
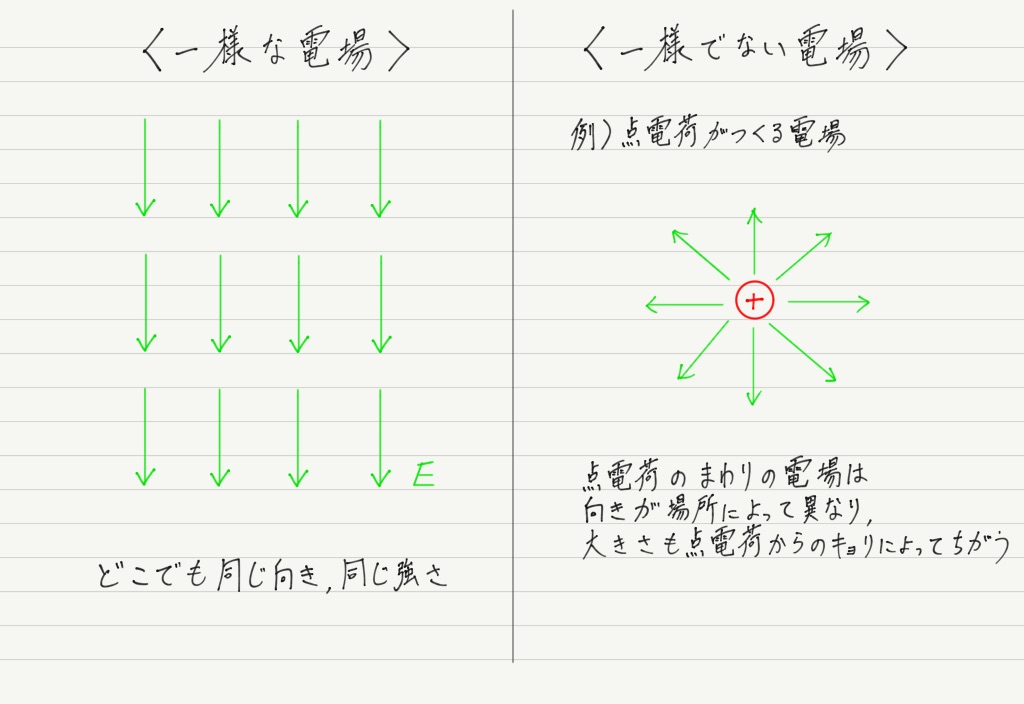
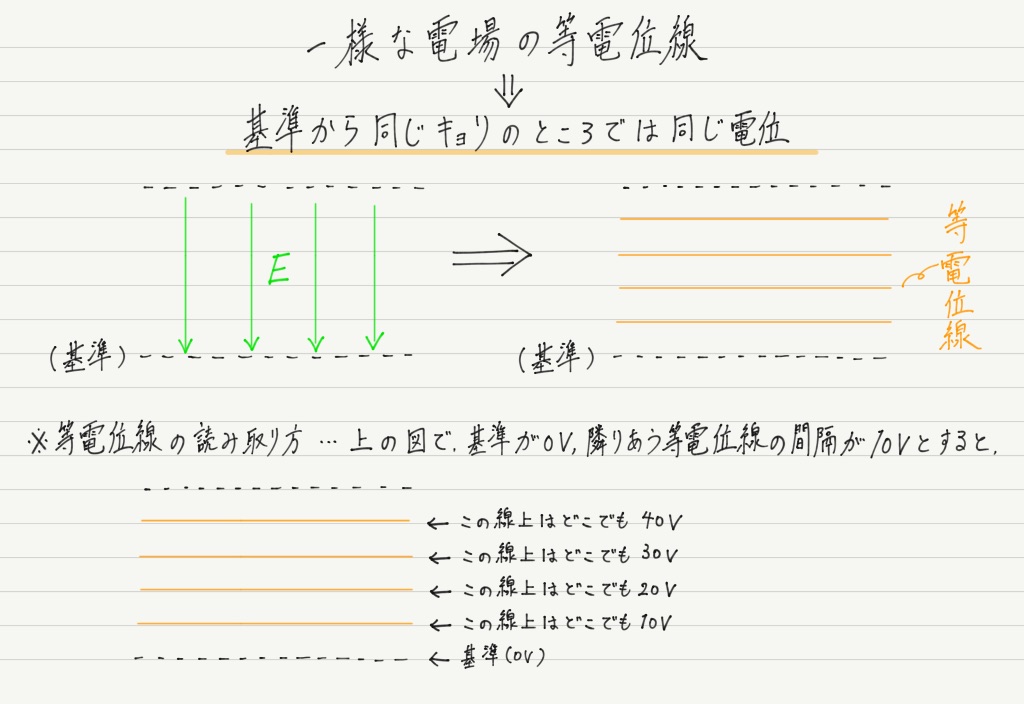
一様な電場の場合
「一様な電場」とは,大きさと向きが一定の電場のことです。
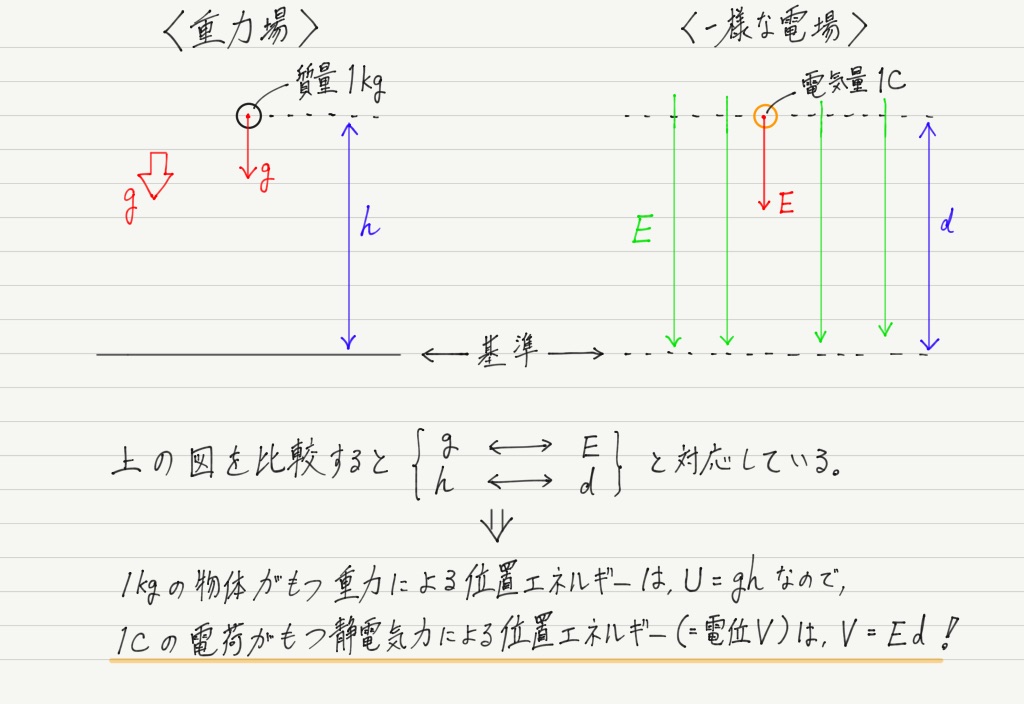
一様な電場と重力場を比較してみましょう。
電位Vと書きましたが,今回は地面(?)を基準に考えているので,「(基準からの)電位差V」が正しい表現になります。
V=Edという式は静電気力による位置エネルギーの回で1度登場しているので,2度目の登場ですね!
忘れている人,また,電位と電位差のちがいがよくわからない人は,ここで一度復習しておきましょう!
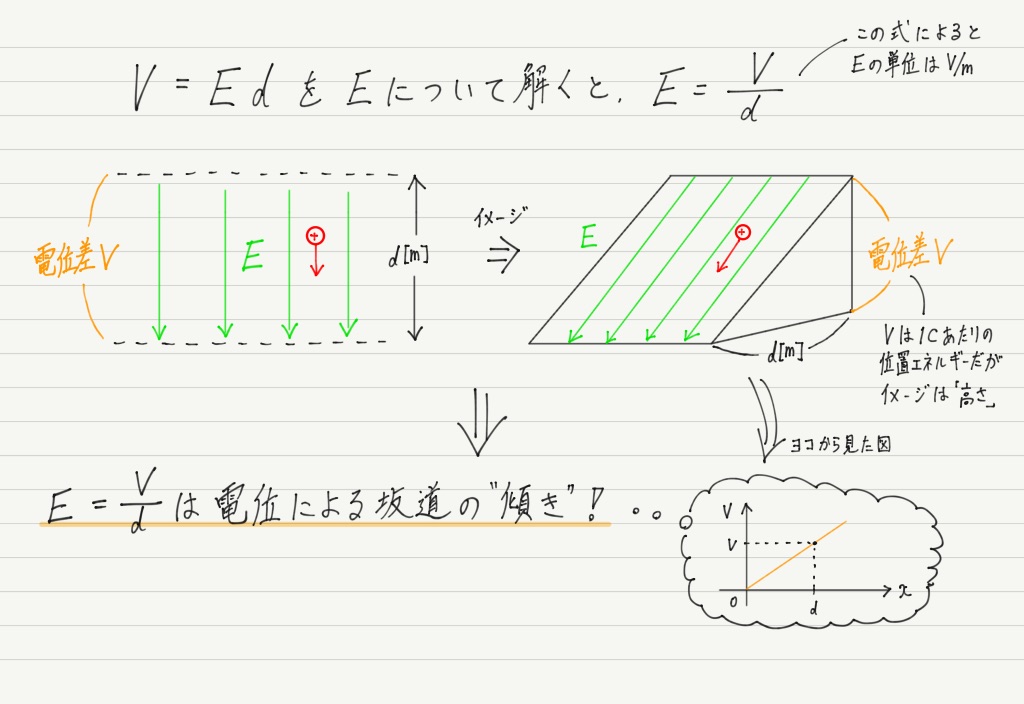
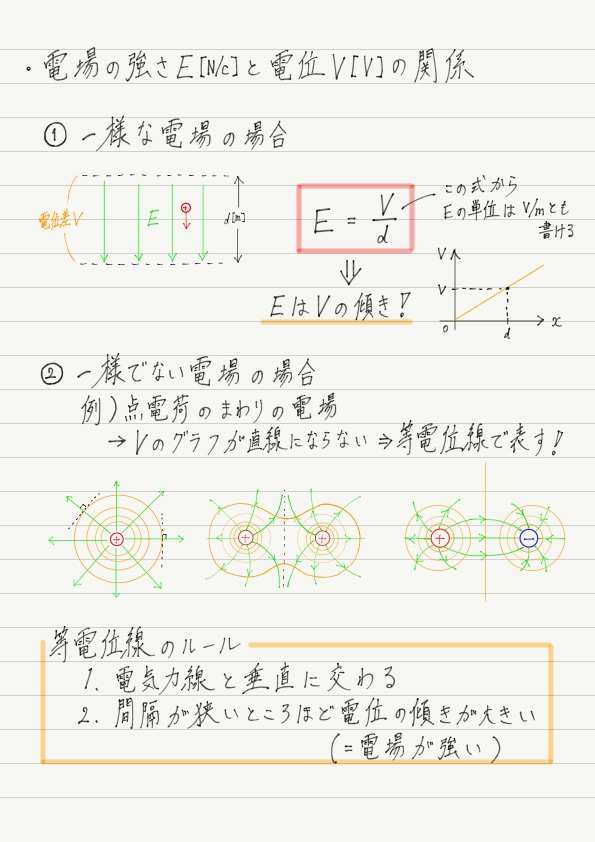
一様な電場Eと電位差Vとの関係式V = Edをちょっとだけ式変形してみると…
電場の単位はN/CとV/mという2種類があるということは,電場のまとめノートにすでに記してあります。
N/Cが「1Cあたりの力」ということを強調した単位だとすれば,V/mは「電位の傾き」を強調した単位です。
もちろん,どちらを使っても構いませんよ!
電気力線と等電位線
いま見たように,一様な電場の場合はEとVの関係は簡単に計算することが可能!
一様な電場では電位の傾きが一定だからです。
じゃあ,一様でない場合は?
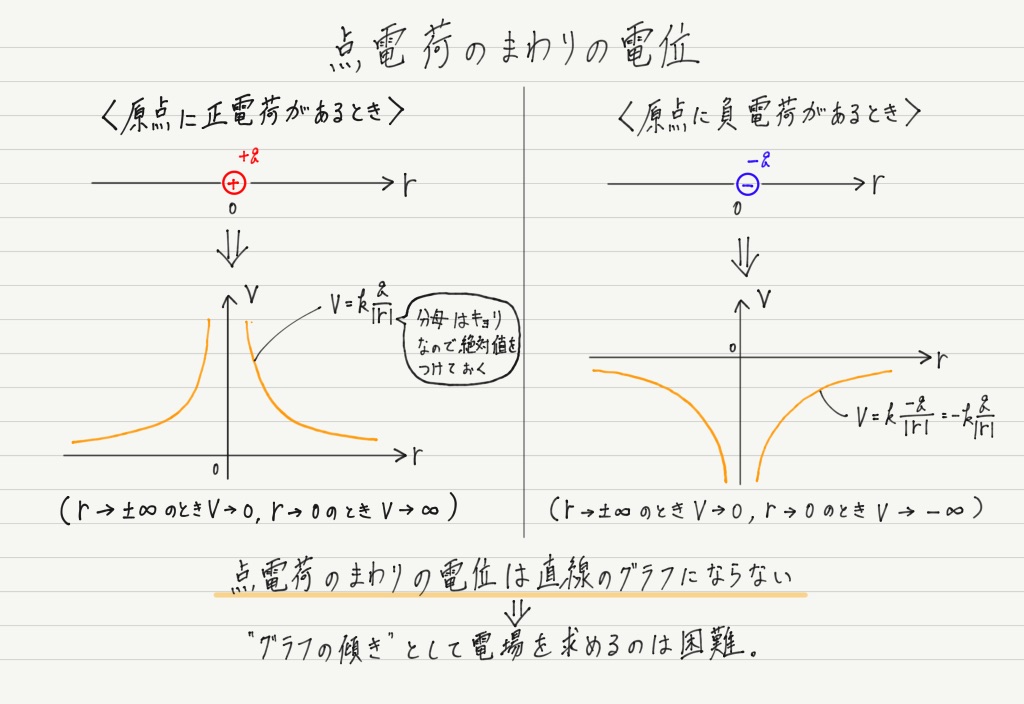
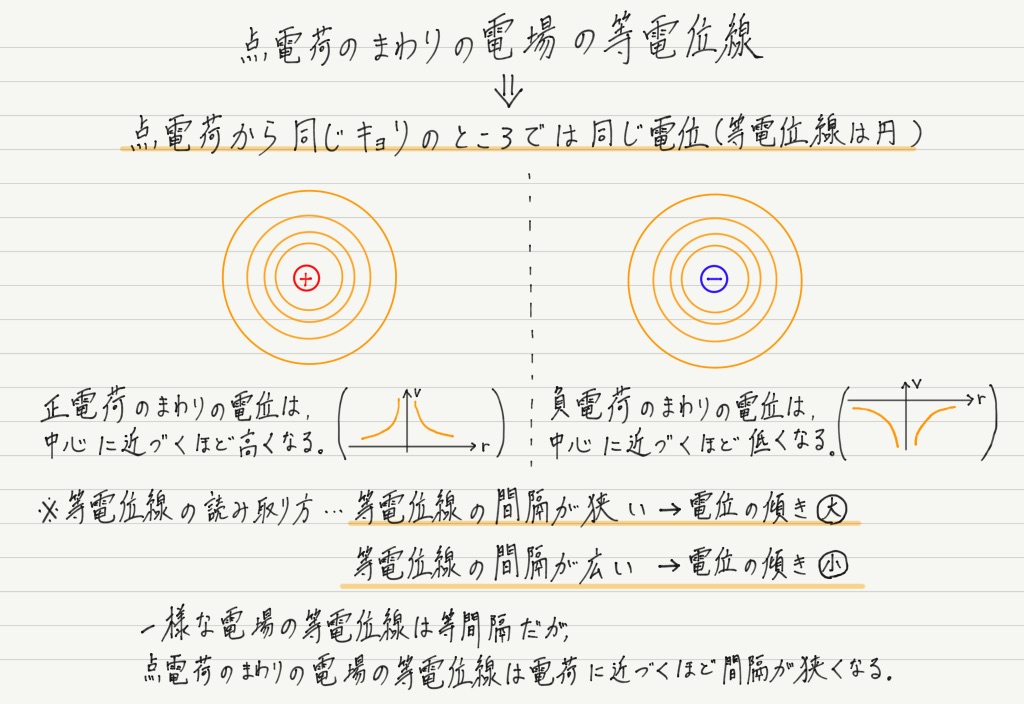
例として点電荷のまわりの電場と電位を考えてみましょう。
この場合も電位の傾きとして電場が求められるのでしょうか? 電位のグラフを書いてみると…
うーん,グラフが曲線になってしまいましたね(^_^;)
このような「曲がったグラフ」の傾きを求めるのは容易ではありません。
(※ 数学をある程度学習している人は,微分すればよいということに気付くと思いますが,このサイトは初学者向けなのでそこまで踏み込みません。)
というわけで計算ではなく,視覚的に捉えることにしましょう。
電場を視覚的に捉えるには電気力線が有効でした。 電位を視覚的に捉える場合には「等電位線」を用います。
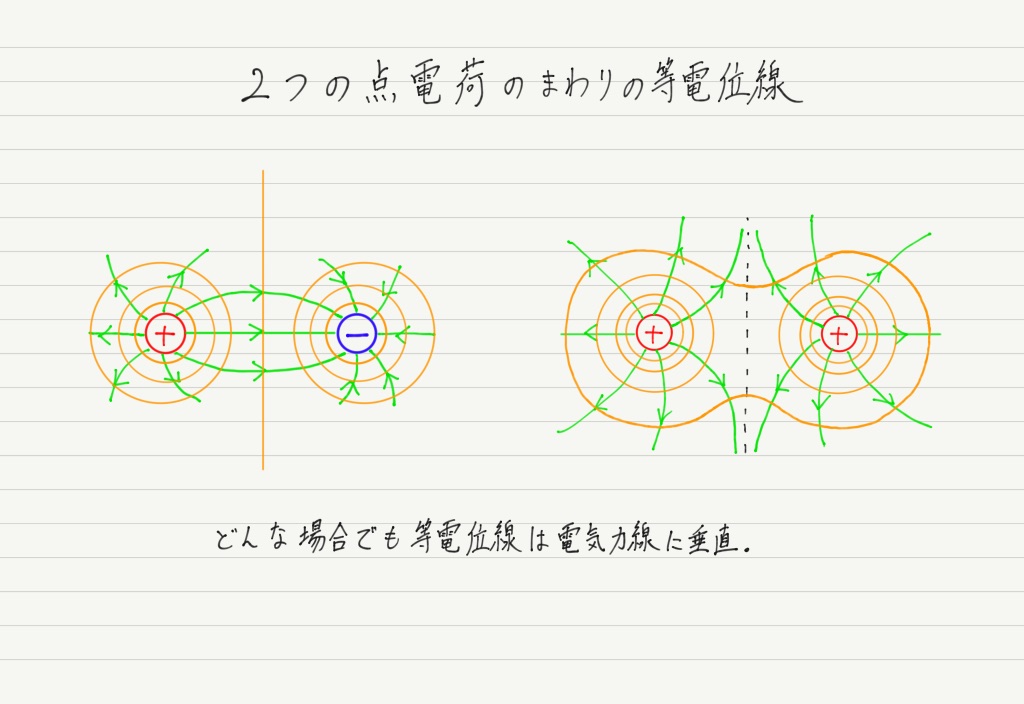
その名の通り,「等しい電位をつないだ線」のことです! いくつか例を挙げてみます↓
もう気づいた人もいると思いますが,等電位線は地図の「等高線」とまったく同じ概念です!
等高線も間隔が狭いほど,急な斜面を表します。
そもそも電位のイメージは “高さ” だったわけで,そう考えれば電位を山に見立て,等高線を持ち出すのは自然です。
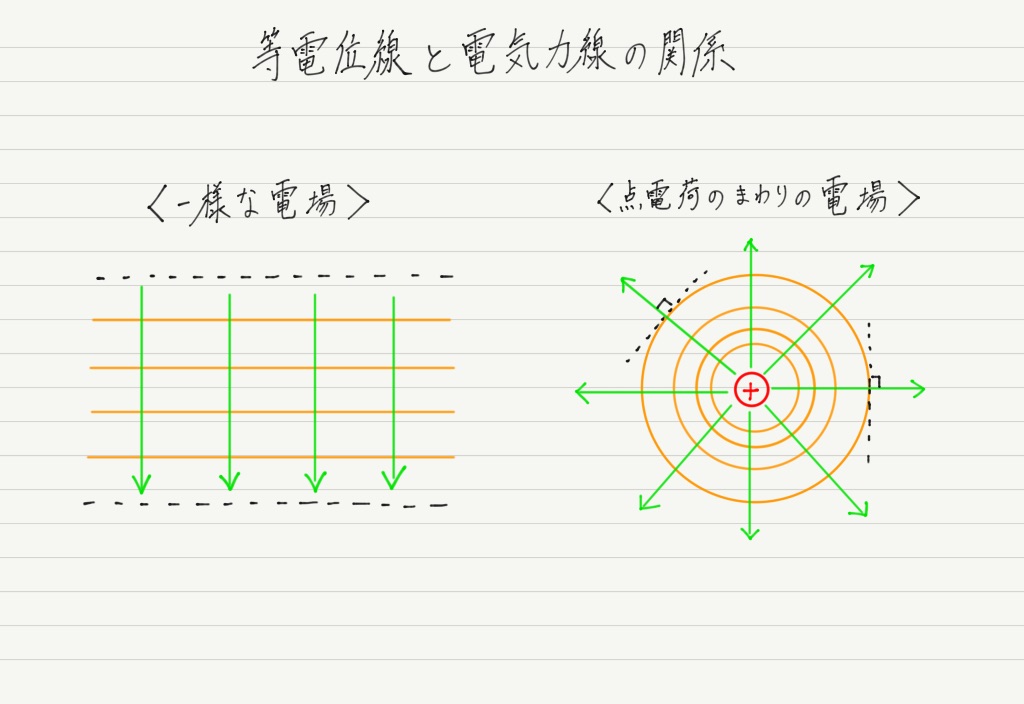
ここで,先ほどの等電位線の中に電気力線も一緒に書き込んでみましょう!
…気付きましたか? 電気力線と等電位線(の接線)は必ず垂直に交わります!!
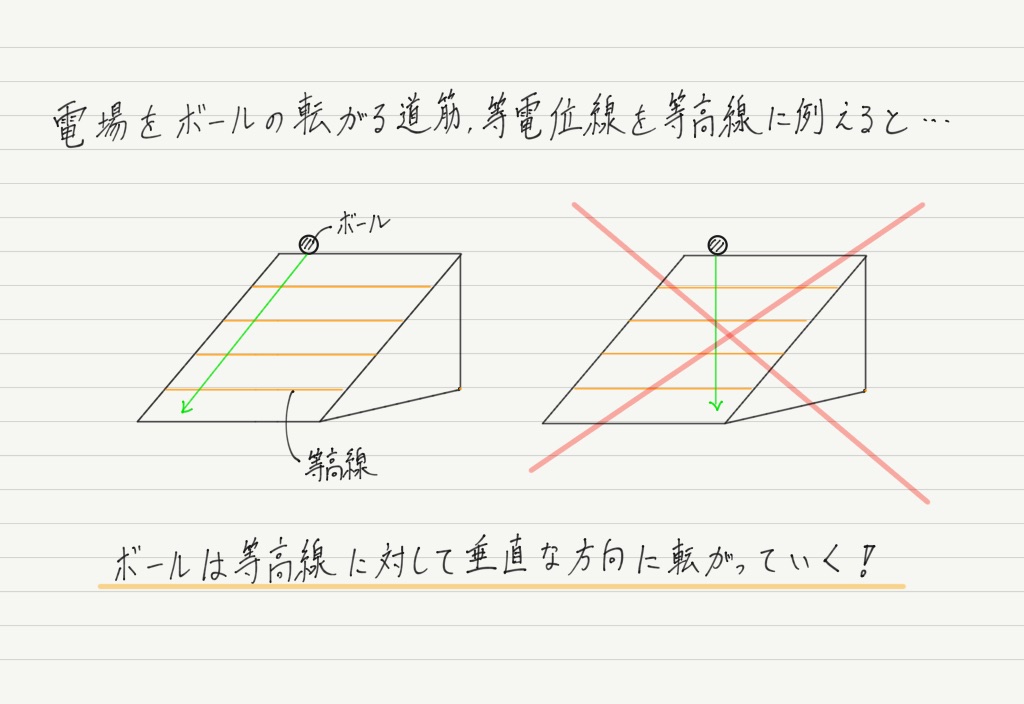
電気力線とは正電荷が動く道筋のことだったので,山の斜面を転がるボールの道筋をイメージすれば,電気力線と等電位線が必ず垂直になることは当たり前!!
等電位線が電気力線と垂直に交わるという事実を知っておけば,多少複雑な等電位線も書くことができます。
今回のまとめノート
電場と電位は切っても切り離せない関係にあります。
電場があれば電位も存在するし,電位があれば電場が存在します。
両者の関係について,しっかり理解できるまで問題演習を繰り返しましょう!
次回予告
電場の中にあるのに,電場がないものなーんだ?
なぞなぞみたいですが,れっきとした物理の問題です。
この問題の答えを次の記事で解説します。お楽しみに!!