こんな波のグラフの問題,見たことありませんか?
この「y-xグラフが与えられていて,それをもとにy-tグラフを書く」という問題,物理基礎の波の分野の中でも特によくわからないと評判(?)です。 今回はこのタイプの問題へのアプローチの仕方を伝授しましょう!!
波のグラフを書くのに必要な情報を集める
よくわからない問題に出会ったときこそ,シンプルに考えましょう。 今回はグラフを書けという問題なので,どうしたらグラフが書けるのかを考えます。
たとえば1次関数のグラフを書けと言われたら,グラフの形は直線だと分かっているので,あとは傾きと切片さえ分かれば書くことができます。
2次関数のグラフなら形は放物線なので,あとは頂点の座標と上に凸か下に凸かさえ分かれば書くことができます。
そして今回書けと言われているのは波のy-tグラフ。 y-tグラフの形は正弦波であることはすでに分かっています。
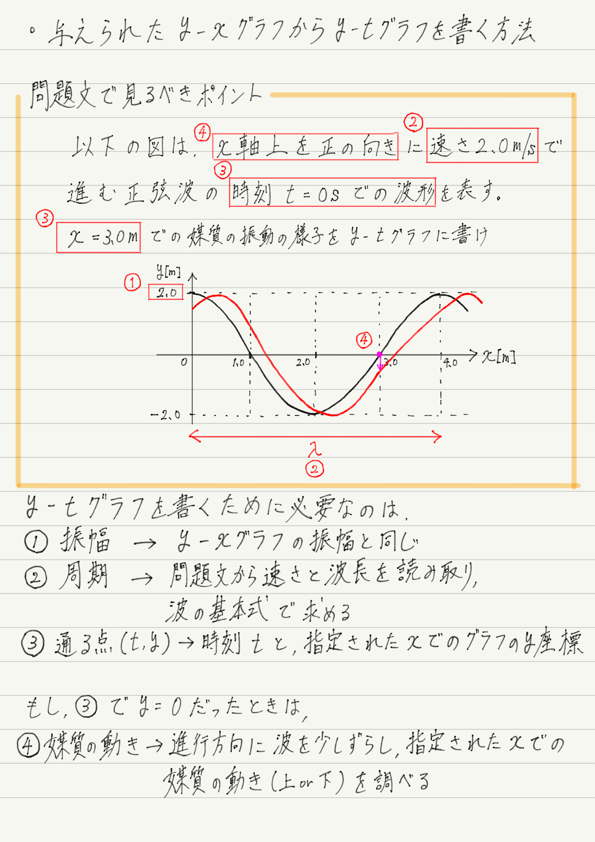
グラフの形が分かっているので,あとは「山の高さ(=振幅)」,「山と山の距離(=周期)」,「通る点」さえ分かれば,グラフが完成します!
問題文のここを見ろ!
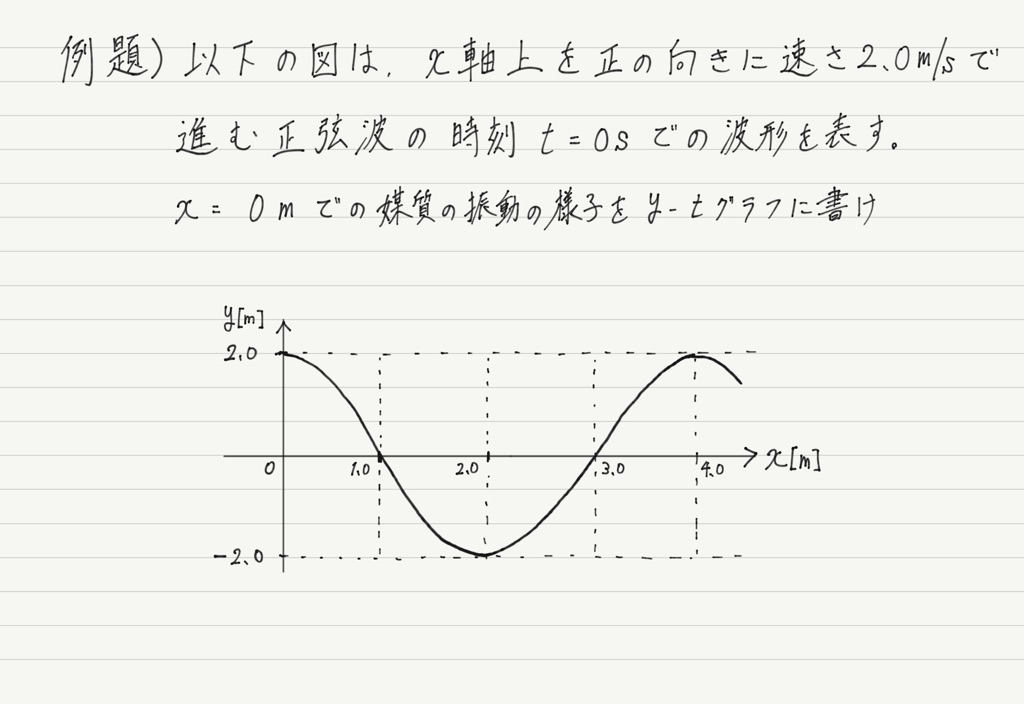
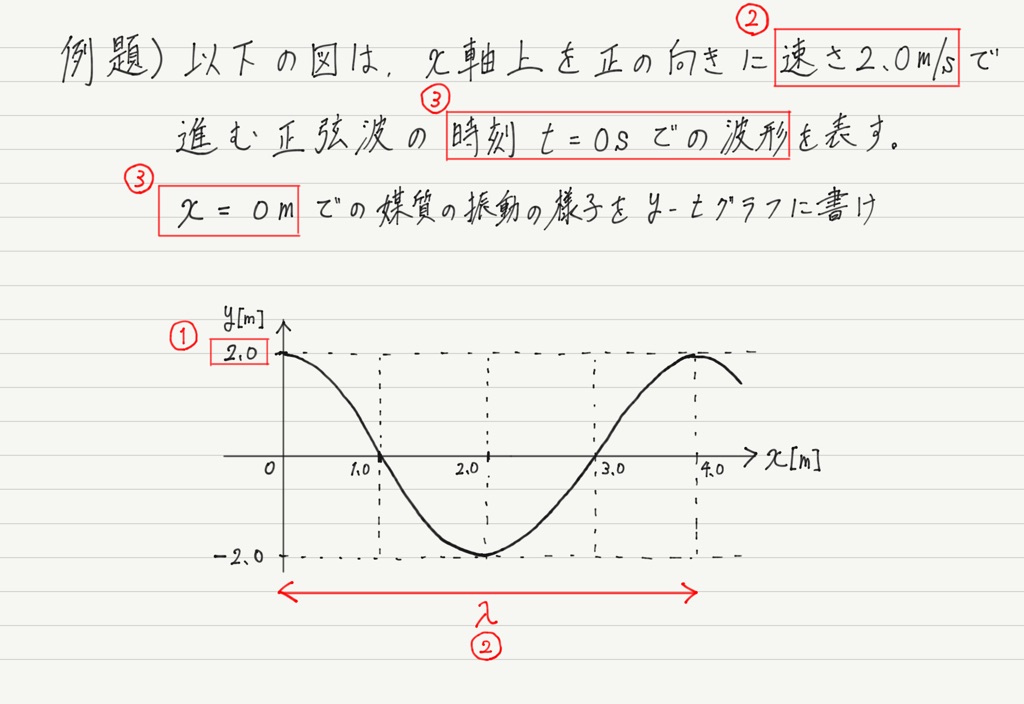
では,①山の高さ,②山と山の距離,③通る点をそれぞれ求めていきます。
どの問題もそうですが,問題文はしっかり読みましょう。
①〜③を求めるのに注目すべき箇所を記しておきます。
ではひとつずつ見ていきましょう。
まず①山の高さですが,波のグラフにおける山の高さとは振幅のことです。
振幅はy-tグラフでもy-xグラフでも共通なので,与えられたy-xグラフの振幅を読み取って,それをそのままy-tグラフの振幅として使います。
次に②山と山の距離ですが,これは①とちがって「y-xグラフの山と山の距離を読み取って,それをそのまま使う」ということはできません!
なぜなら,y-xグラフの山と山の距離=波長なのに対し,y-tグラフの山と山の距離=周期だからです。
y-tグラフを書くためには波長ではなく周期が必要ですが,問題文には書いてありません。
書いてなければ計算で求めるまで。 そう,波の基本式ですね!
これで周期が求められました。
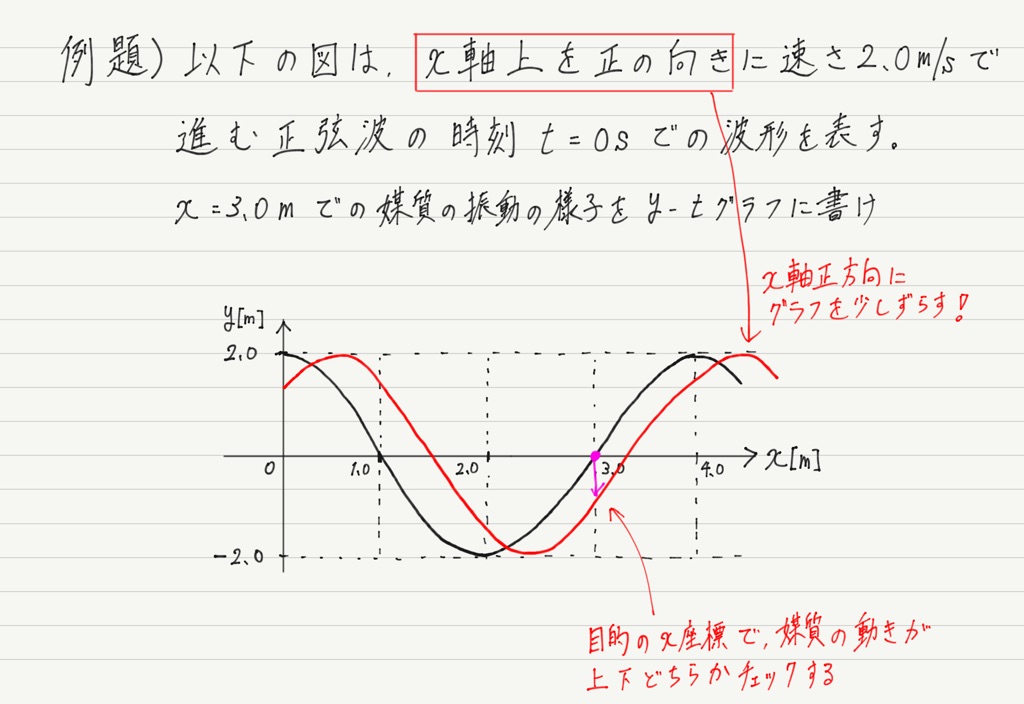
最後に③の通る点です。 このタイプの問題は,問題文に必ず「x=◯◯での振動の様子を〜」と書いてあるので,そこに注目します。
問題文で指定されたxにおけるグラフのy座標(波の高さ)を読み取りましょう。
今回の問題は「x=0mでの〜」とあるので,x=0mでの波の高さを読み取ると,y=2.0mです。
さらにもうひとつ,問題文で注目すべき箇所があります。 それは,「時刻 t=◯◯での波形〜」という部分。 y-xグラフとは波の “写真” に例えられるのでした。
問題文のt=◯◯とは,カメラのシャッターを押した時刻です。 この情報がなければy-tグラフは書けません。
今回は時刻t=0sとあります。
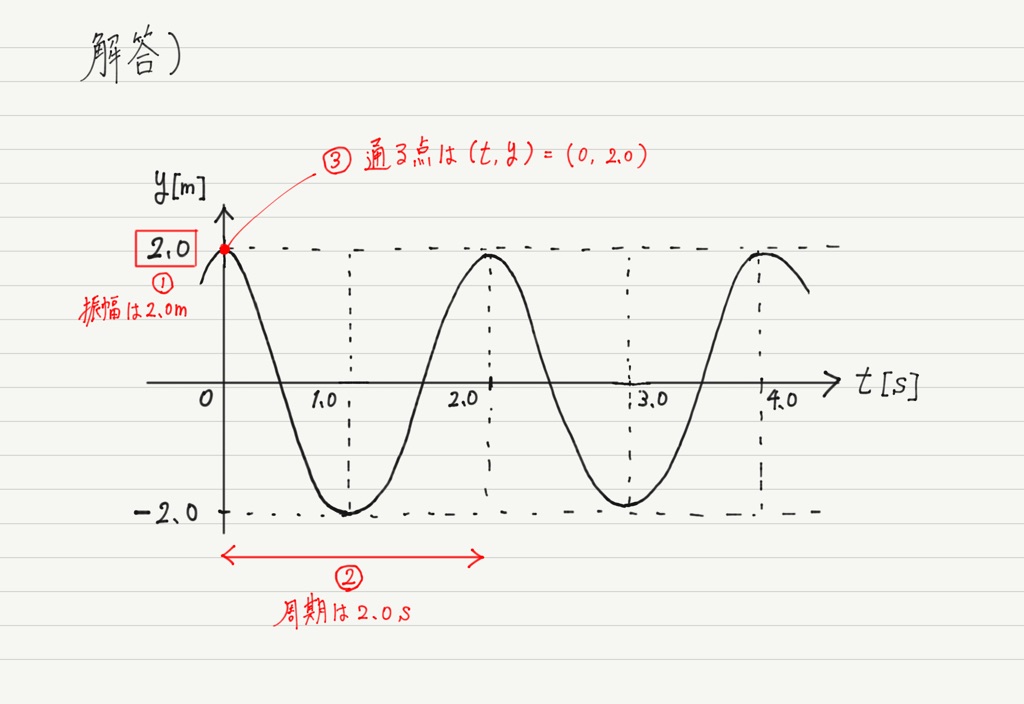
先ほどの座標の情報と合わせると,この問題文とグラフからは「時刻 t=0sのとき,x=0mでの波の高さは y=2.0m」という情報が読み取れます。
ただ,今回私たちが書きたいのはy-tグラフなので,xに関する情報は消してしまいましょう。
すると,「時刻 t=0sのとき,波の高さはy=2.0m」となります。 これがy-tグラフの通る点です!
以上をまとめると,答えは,
となります。
もう1つの例題
上で学んだことをもとに,もう1問やってみましょう。
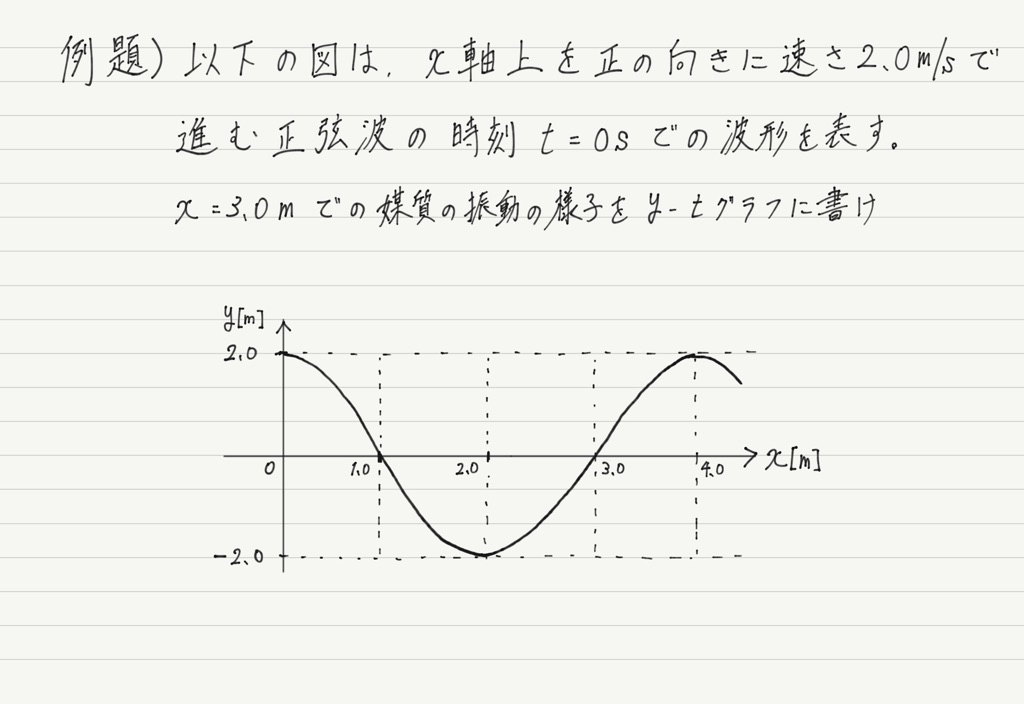
先ほどと同じ設定ですが,x=◯◯の部分を変えてあります。
さっきと同じやり方で必要な情報を読み取っていくと,
①山の高さ(振幅)→ 2.0m
②山と山の距離(周期)→ 2.0s
③通る点 → 時刻t=0sのとき, y=0m
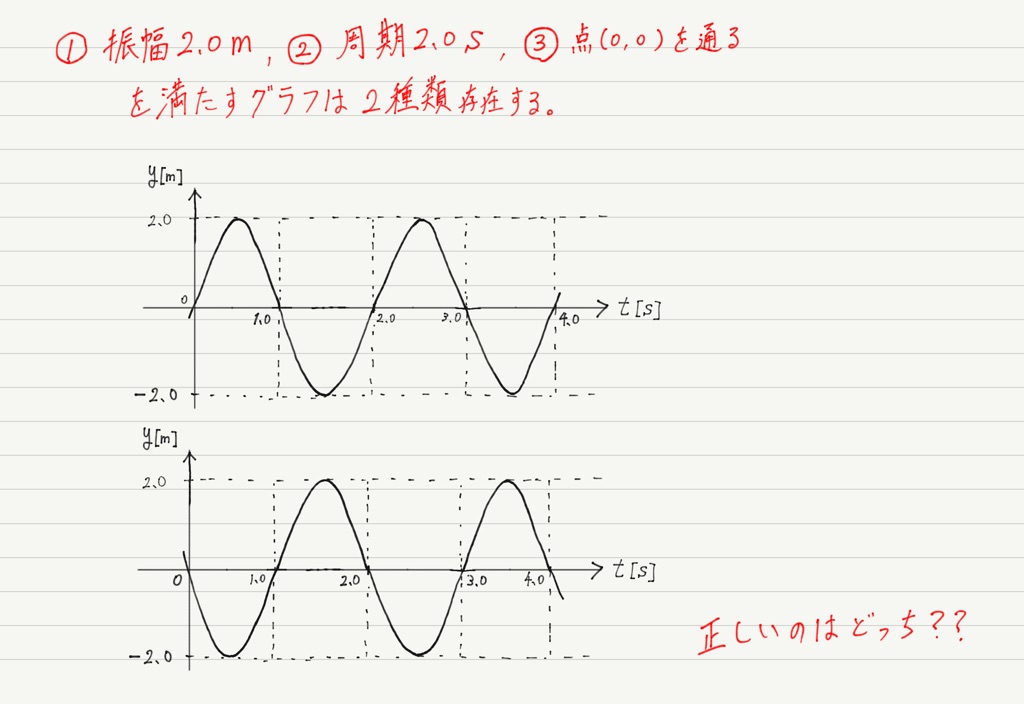
となりますが,今回はこれだけではグラフが書けません。
なぜなら,上の①〜③の条件を満たすグラフは1つではないからです!
最初にやった例題のように,通る点が山(or 谷)ならそのままグラフが書けますが,今回のように通る点が真ん中(y=0)にある場合は,次の瞬間にグラフが上に行くのか,それとも下に行くのか,得られた情報だけでは判断できません。
これは1つのアイデアで解決できます。 前回の補講を思い出してください。
この補講で学んだ,「グラフを進行方向に少しずらす」という方法を使えばうまくいきそうじゃないですか?
実際にやってみましょう。
今回はx=3.0mにおけるy-tグラフを書きたいので,与えられたグラフを進行方向に少しずらします(問題文の進行方向はこのために書いてある!)。
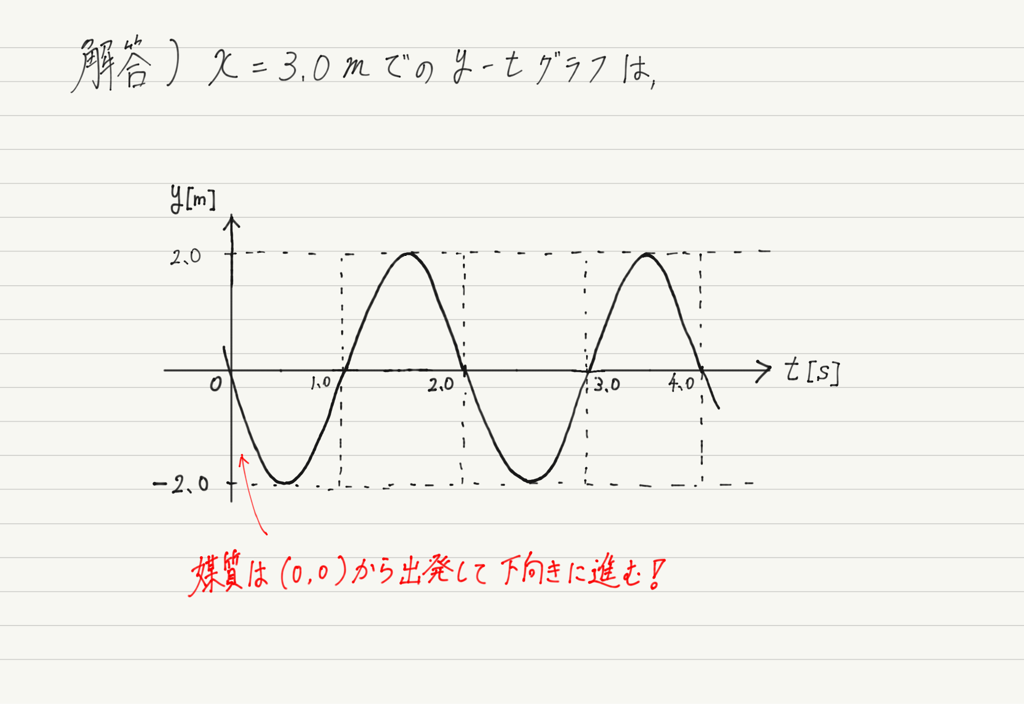
この図の通り,x=3.0mの地点にある媒質は次の瞬間には下に動くことが分かります。
よって正解のy-tグラフは,
となります!!
今回のまとめノート
説明は長くなってしまいましたが,問題文の見るべきポイントを押さえれば,実際に問題を解くのはそれほど大変ではないはず。 類題を解いて慣れてしまいましょう!