今回と次回は波をグラフで表すことを考えましょう!
なぜ2回分使うのかというと,波のグラフは一筋縄ではいかないから。 これまで皆さんが数学で習ってきた,いわゆる “普通のグラフ” とは異なる点があるのです。
1変数関数と2変数関数
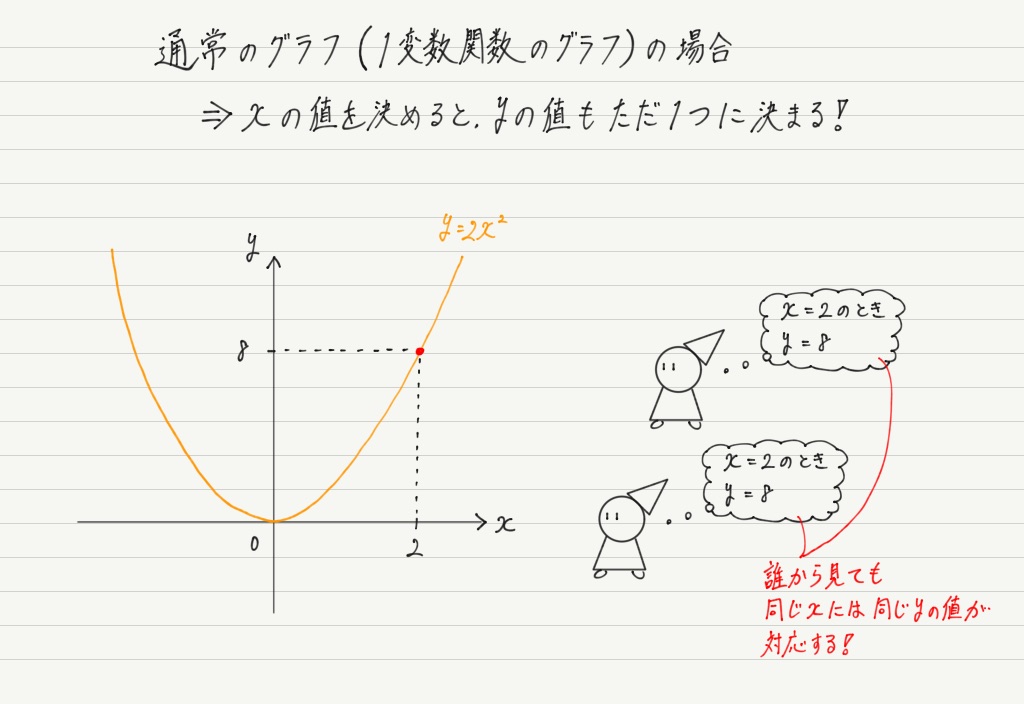
まず “普通のグラフ” についておさらいしましょう。
これは「xの値を決めると,それに対応するyの値がひとつ決まる」という性質があります。
これを関数,特に「1変数関数」と呼びます。
高校までの数学で習う関数はすべてこの1変数関数です。 これに対して,波のグラフはどうでしょうか。
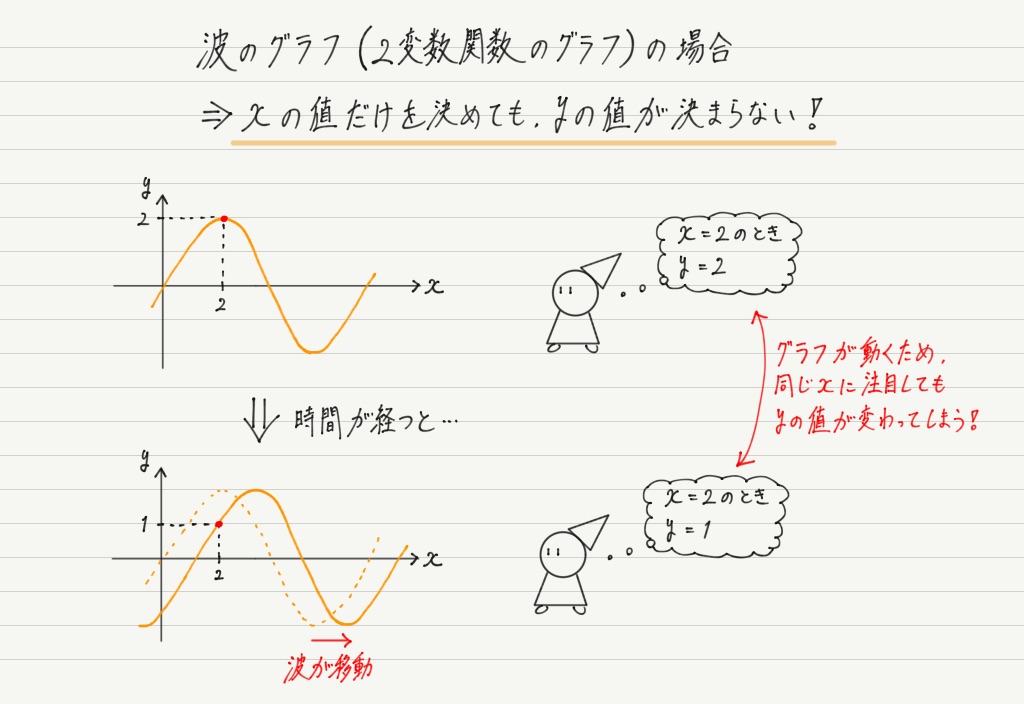
このように,波のグラフの場合はxを決めたとしても,yの値が決まりません! これは大変!
原因はもちろん波が動いていること。 つまりyの値をちゃんと伝えようと思ったら,xの値だけではなく,そのグラフを見た時刻まで言わなければいけないのです!!
まとめると,波のグラフではyの値を決めるためには,x(位置)とt(時刻)という2つの変数を指定する必要があります。
このような関数を「2変数関数」と言います。
波のグラフをどう書けばいいか
波のグラフが普通のグラフとちがうということが分かってもらえたと思います。 ゴチャゴチャ説明しましたが,要するに「波は動くので,そのままグラフにはできない」ということです。 動くグラフなんて書きようがありません。
しかし,書けないから書かないというのでは話が進まないので,どうにかして書くことはできないか考えてみましょう。
もとを正せば,波のグラフが書けない原因は変数が2つあるから。 もし変数が1つならば,いつも数学でやっている通り,グラフを書くことができます。
そこで,波のグラフを書くためにこのように考えます。
「本当は変数が2つあるけど,片方を定数だと思ってしまえ!!」
変数を定数だと思っていいのか?と疑問に感じる人もいると思いますが,思うのはその人の勝手!
ともかく,2つあった変数のうち1つを定数ということにしてしまえば,変数が1つ減って,いつもの1変数関数として取り扱うことが出来ます。
y-xグラフの意味
さあ,これでようやく波のグラフが書けます!
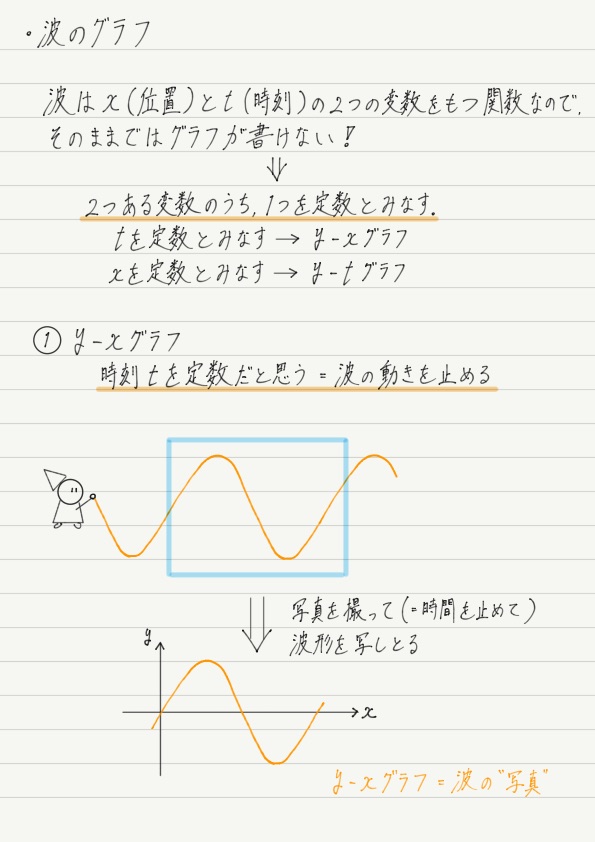
まずは2つある変数のうち,t(時刻)を定数だと思うことにします。
時刻を定数にするということは,すなわち「時を止める」ということですが,難しく考えず,「動く波を写真に収めた」と思ってください。
写真の中では波は動きません。 つまり時が止まったのと同じです。 止まっていればグラフにすることができる!
たとえば,時刻t=5sでのy-xグラフを書けと言われたら,時刻を数え始めてから5秒後の波を写真に撮れば,それが求めるy-xグラフということになります。
写真に写った波形をそのままグラフにしたものがy-xグラフ。
ここまでの内容をまとめておきましょう。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
長くなりましたので,この話の続きは次回に持ち越します!