本編の波のグラフの読み取りでは振幅や波長など，数値の読み取りをメインとして解説しました。
今回は数値ではなく，媒質の動きを読み取ってみましょう。
例題
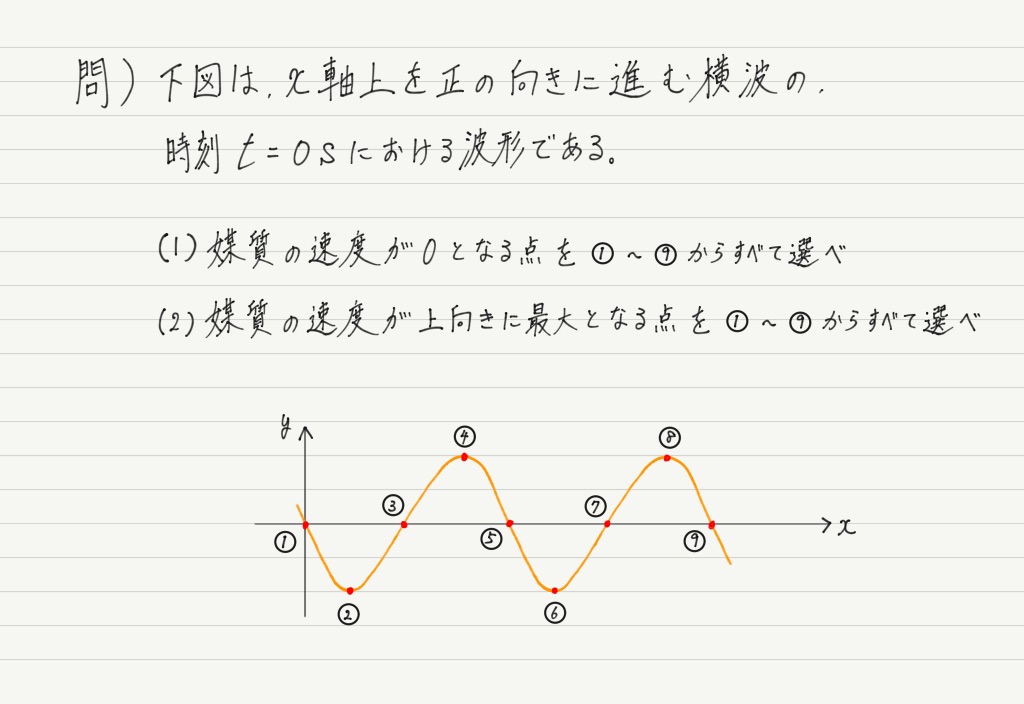
今回扱う問題はこれです！
数値を問われているわけではないので，グラフのどこを見ればいいのかわからない！という人が多いです。 さっそく解説していきましょう！！
問われているのは “媒質の” 速度
まず，問題文をよく読まずに勘違いしている人へ。
この問題で問われているのは “媒質の” 速度であって，波が進む速度ではありません！！
そもそも波は（媒質が変わらなければ）等速で運動するので，速度が0になる場所なんてありません。
媒質の速度を聞かれているということは，波の動きではなく媒質の動きに注目すればOK！ いつものロープを伝わる波の例もいいですが，媒質の動きが一番わかりやすいのはコレ↓
これはウェーブマシンと呼ばれる実験装置です。すだれのように並べられた棒が揺れを伝えて，波を観察することができます。
学校の授業で見たことがある人はその動きを思い出してください。 見たことがないという人はYouTubeで検索すれば動きを見ることができるので，一度確認してください！
ウェーブマシンの動きは頭に入りましたか？
では（1）から。媒質の速度が0になる点ということですが，ウェーブマシンの媒質とは並んだ1本1本の棒のこと。
つまりこの問題を解くには，「ウェーブマシンの棒の動き」に注目すればいいのです！
ウェーブマシンを見るとどうしても「全体の動き（＝波の動き）」を見てしまいがちですが，ぐっとこらえて「1本の棒の動き」だけを追ってください。
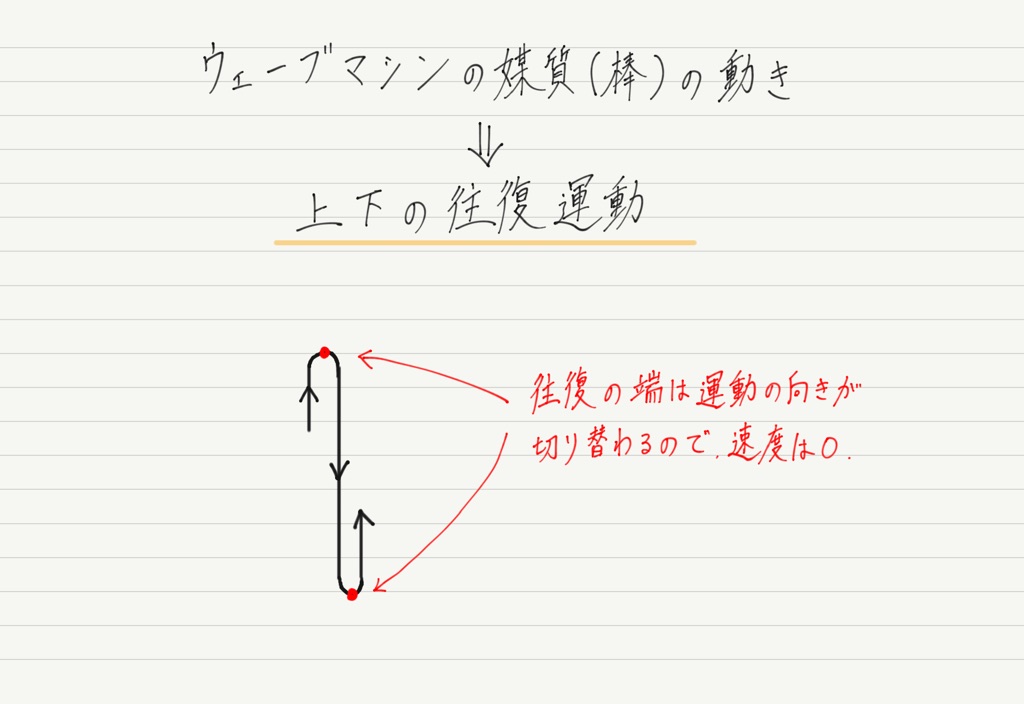
すると，棒は上下に往復しているだけということに気づくと思います。 これに気づけば問題はもう解けたようなもの。
往復運動の中で速度が0になる地点は一番上と一番下に決まっています！！
よって（1）の答えは，波の一番上（山）と一番下（谷）。 ②，④，⑥，⑧が答えです！
媒質の動く向きの調べ方
次に（2）。 今度は上向きの速度が最大となる場所を探します。 （1）で，一番上と一番下で速度が0だと分かりました。
これは，「上に行くと減速して，一番上で一瞬静止する。また，下に行っても減速して，一番下で一瞬静止する。」ということを意味しています。
上に行っても下に行っても減速するのなら，一番速く動いているのはどこでしょうか？
そりゃもちろん，ど真ん中ですよね！！
よって，速さが最大の点は x軸との交点，①，③，⑤，⑦，⑨になります。
まだ終わりじゃありません。 問題は「上向きの速度が最大となる点」なので，向きも考えなければいけません。
さぁ，考えてみよう！ …と言いたいところですが，これはやり方を知らないと多分できないやつ笑
もちろんグラフから読み取るのですが，y-xグラフとは動いている波の時間を止めて書いたグラフ（＝波の “写真” ）なので，媒質がどう動いているかなんてわかるはずありません。
解決策は「次の瞬間の写真を撮って比較する」です！
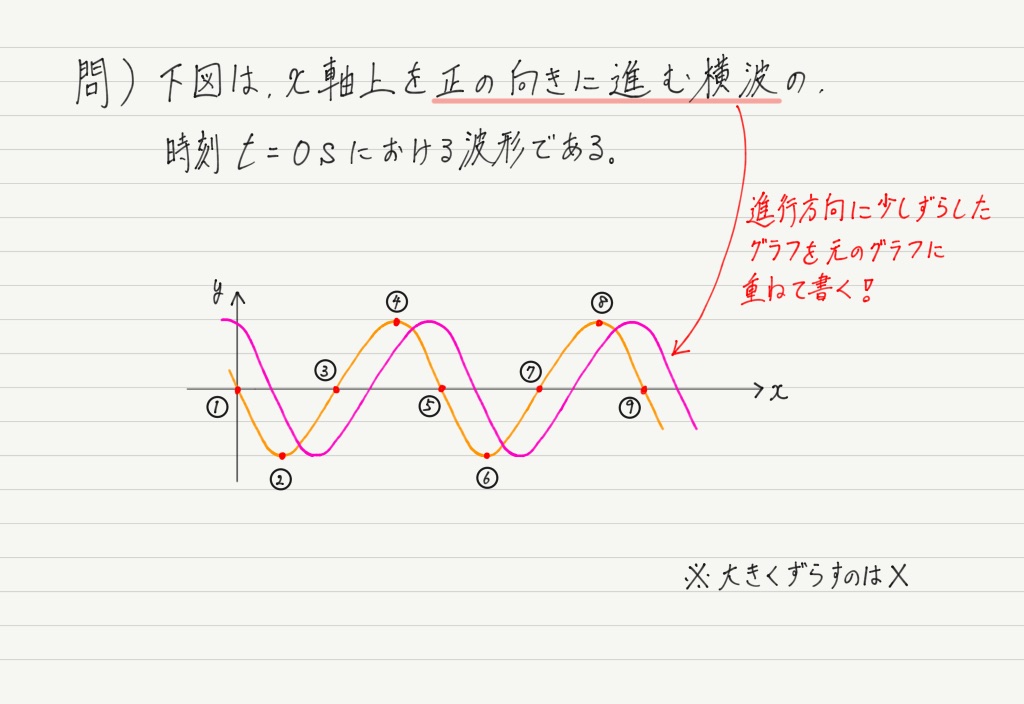
もちろん写真は比喩なので，具体的には次の瞬間のy-xグラフを書きます。 問題文に波の進行方向が記されているので，この方向に波を少しだけずらしてみましょう！
問題文に与えられたグラフは “ある瞬間の” 波形で，ずらして書いたのが “次の瞬間の” 波形になります。
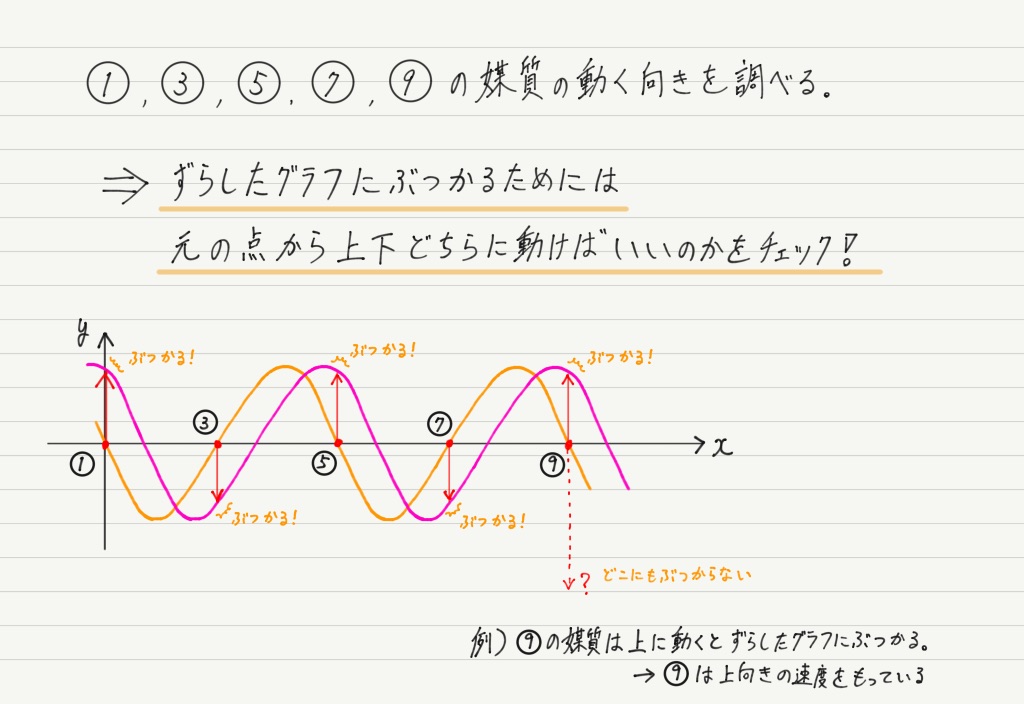
では，このグラフがウェーブマシンの波を表していると思ってください。 最初にある波が動いた結果，ずらした波になるわけですが，①，③，⑤，⑦，⑨にある棒の動きはどうなるでしょう？
棒は上下にしか動けないことを忘れずに。
これでそれぞれの棒が上下どちらに動いたのかが分かりましたね！
（2）の答えは速さが最大の①，③，⑤，⑦，⑨のうち，矢印が上を向いているもの。つまり，①，⑤，⑨です！
上の例では横波を扱いましたが，横波表示された縦波のグラフも全く同様に考えることができます。
ただし縦波のグラフは，本来ならx軸に沿った変位を，むりやりy軸方向にして書いたものなので，そこだけ注意が必要です。
もし先ほどの例題が縦波なら，（２）の答えは「媒質の速度が右向きに最大となる点」を表します（縦波の右方向はグラフに書くときは上方向になっていることに注意）。
波の問題の中には今回のように，媒質の動きをしっかり理解していないと解けない問題もあります。 ロープでもウェーブマシンでも何でもいいので，媒質の具体的な動きを常に頭に思い描けるようにしておきましょう！
演習問題も用意してあるので，ぜひチャレンジしてみてください！ より一層理解が深まります。
