剛体の運動は一見すると複雑に見えます。 例として三角定規の斜方投射を考えてみましょう。
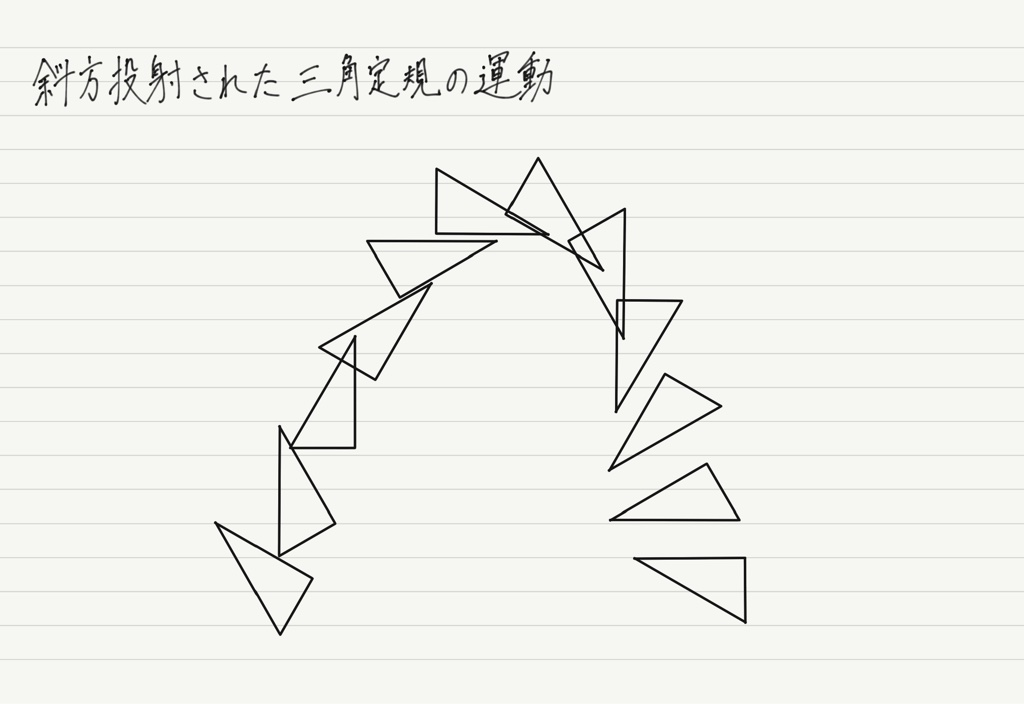
空中に放り投げられた三角定規は下図のように回転しながら落下します。
ね? すごくめんどくさい運動に見えるでしょ?
このような運動を調べる方法は存在するのでしょうか?
これまでに学んだ知識をフル活用して考えてみましょう。
重心に着目せよ
剛体の運動がこのように複雑に見える原因はもちろん,剛体が大きさ(と形)をもっているから。
もし大きさがなければ,つまり斜方投射されたのが三角定規ではなく質点だったら,ただの放物運動ということになってめちゃくちゃ簡単ですよね?
さぁ,ここで重心の回で学んだことを思い出してください。
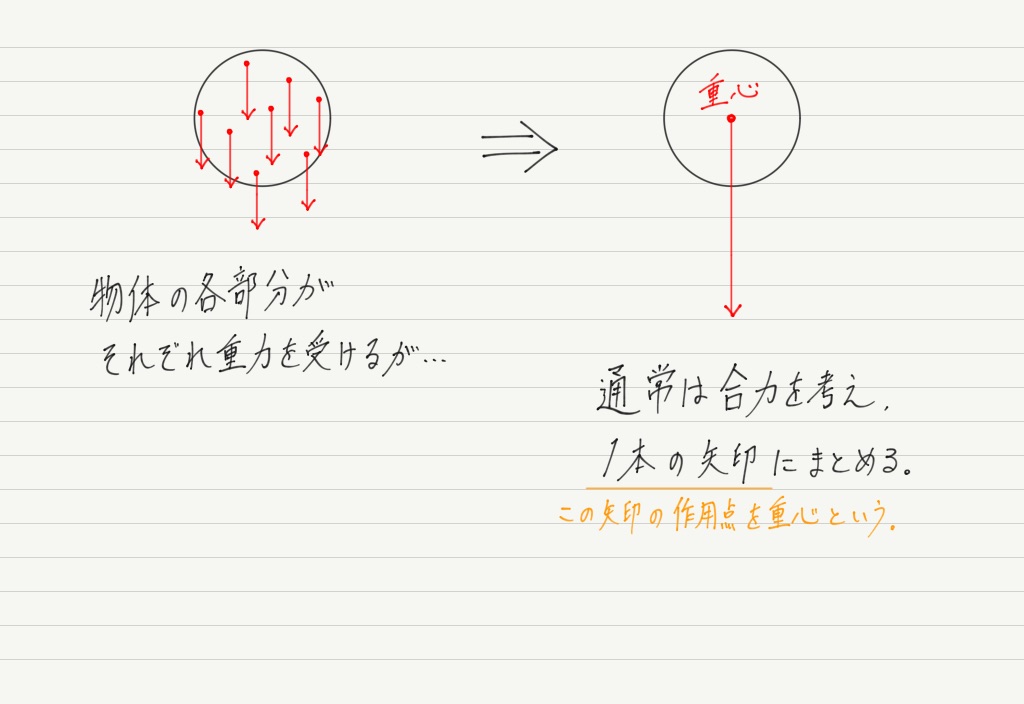
重力は本当は物体の各点にはたらいていますが,物体の質量がすべて重心に集まっていると考えて,「重心にのみ重力がはたらいている」とみなしてOKなのでした。
つまり重心とは,その物体を代表する特別な点と言えるわけです。
ここで斜方投射された三角定規の話に戻りましょう。
三角定規の全体を見るとたしかに複雑な運動に見えますが,重心のみに注目すると…
なんと! 重心だけに注目するときれいに放物運動をしているのです! 質点と同じ運動!
このように一見複雑に見える剛体の運動ですが,その重心に着目すると案外単純な運動をしていたりします。
さて,この三角定規の重心以外はどんな運動をしているでしょうか?
重心の運動についてはもうわかったので,重心は除いて考えたい…!
そんなときに便利なのが相対運動の考え方。 つまり,三角定規の重心に観測者がいると想像するのです。
すると観測者自身は「自分は静止している」と思えるので,その観測者からは純粋に三角定規の重心以外の運動を観測できます!
(相対運動がよくわからない人はこちらの記事で復習してください。)
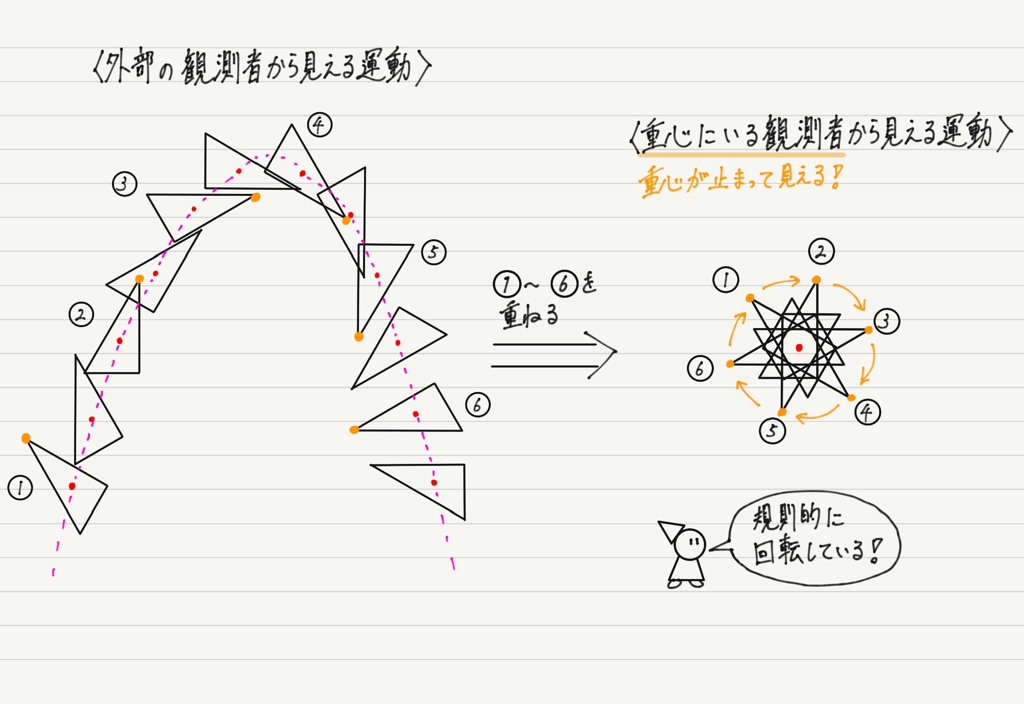
では,重心にいる観測者から三角定規の運動がどう見えるかを調べてみましょう。
この観測者からは重心が止まって見えるので,重心を重ねてみるのがよさそう。
このように,重心にいる観測者からは三角定規が一定のペース(=一定の角速度)で回転して見えるのです!
つまり,重心以外は回転運動ををしていたということになり,これまた非常にシンプルな運動ですね!
このように,剛体の運動は一見すると複雑に見えるけれど,重心とそれ以外の部分で分けて考えると,実は単純な運動になっていたりするのです。
重心から見た物体系の運動
「運動を重心とそれ以外に分けて考える」という方法が使えるのは剛体に限った話ではありません。
この方法が最も威力を発揮するのは物体系の運動を扱うときです!
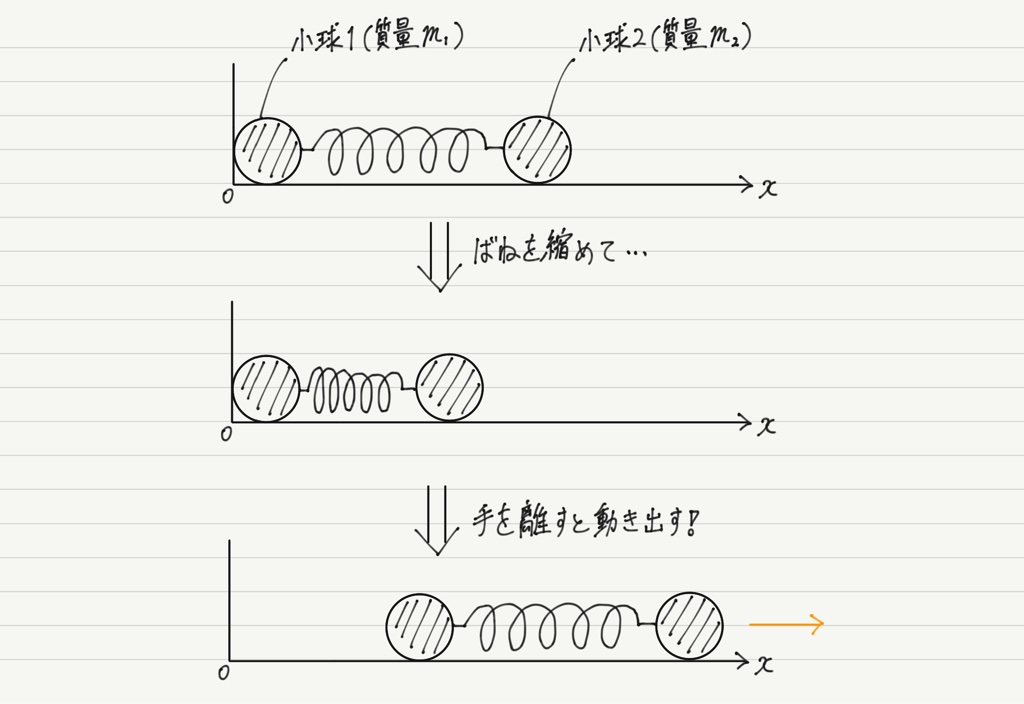
物体系の例として,2つの小球をばねでつないだものを考えてみましょう。
一端を壁につけ,ばねを縮めて手を離すと,ばねが伸び縮みを繰り返しながら運動を始めます。
この運動もまた,一見するとけっこう複雑。
物体系全体を見れば右向きに進んでいきますが,それぞれの小球を見るとばねによって振動しているからです。
そんなわけではまずはこの物体系の重心に着目してみましょう。
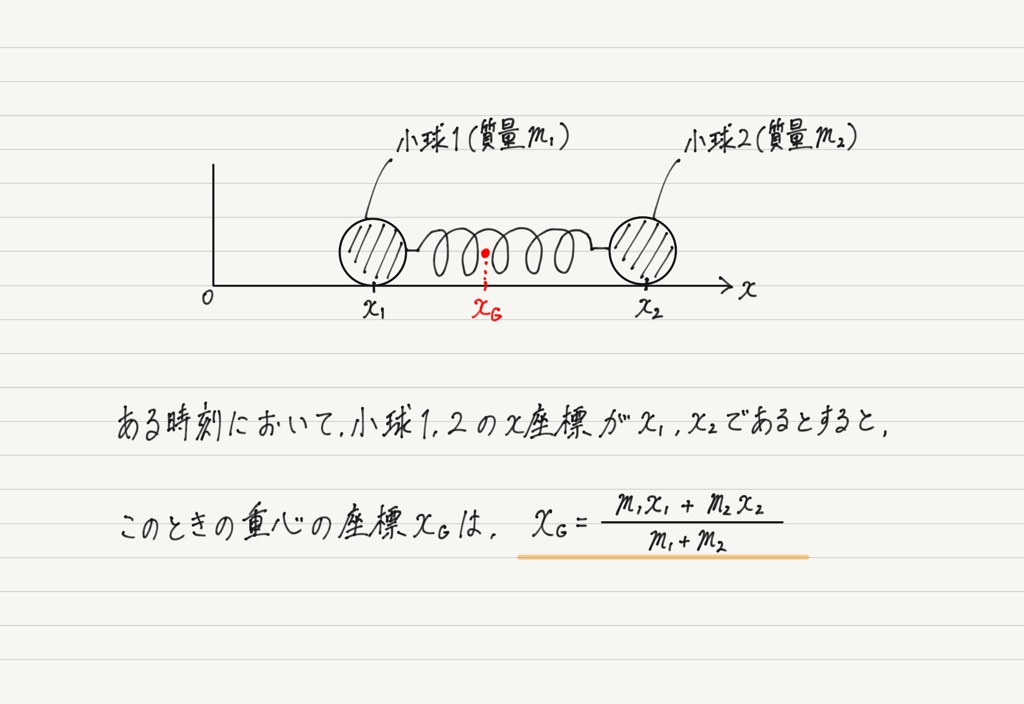
…おっと,その前に重心の場所を求めるのが先ですね。
重心がどこにあるのかわからないと着目できません。
重心の場所がわかったところで(公式に当てはめただけですが笑),重心の運動を調べていきましょう!
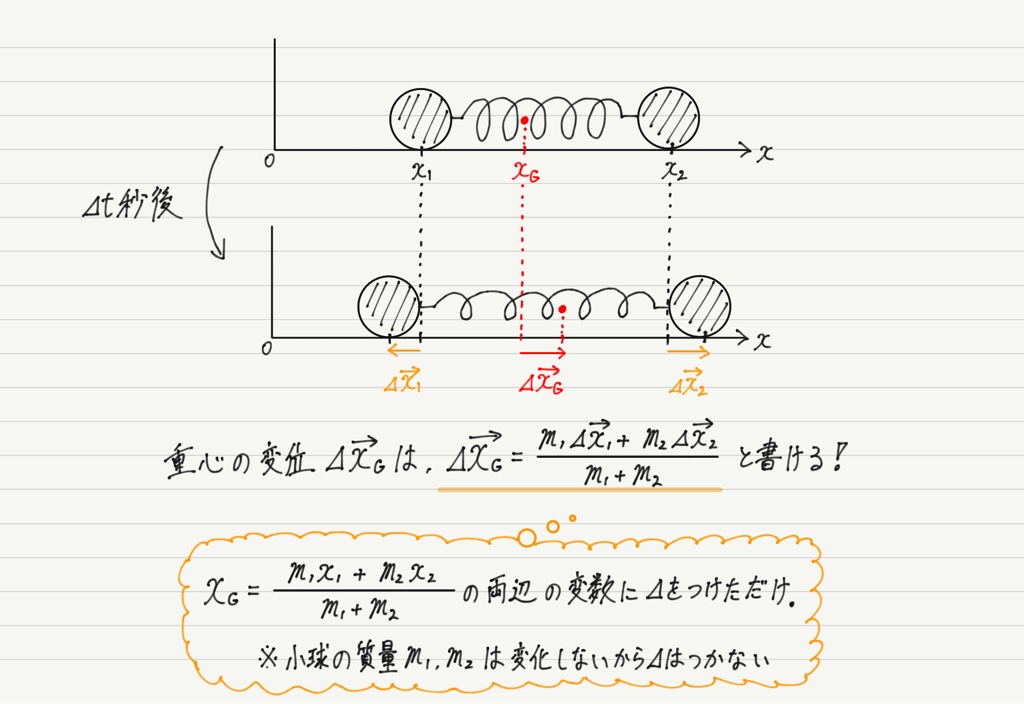
重心の⊿t秒間の変位⊿xGは,小球1の変位⊿x1と小球2の変位⊿x2を用いて次のように表せます。
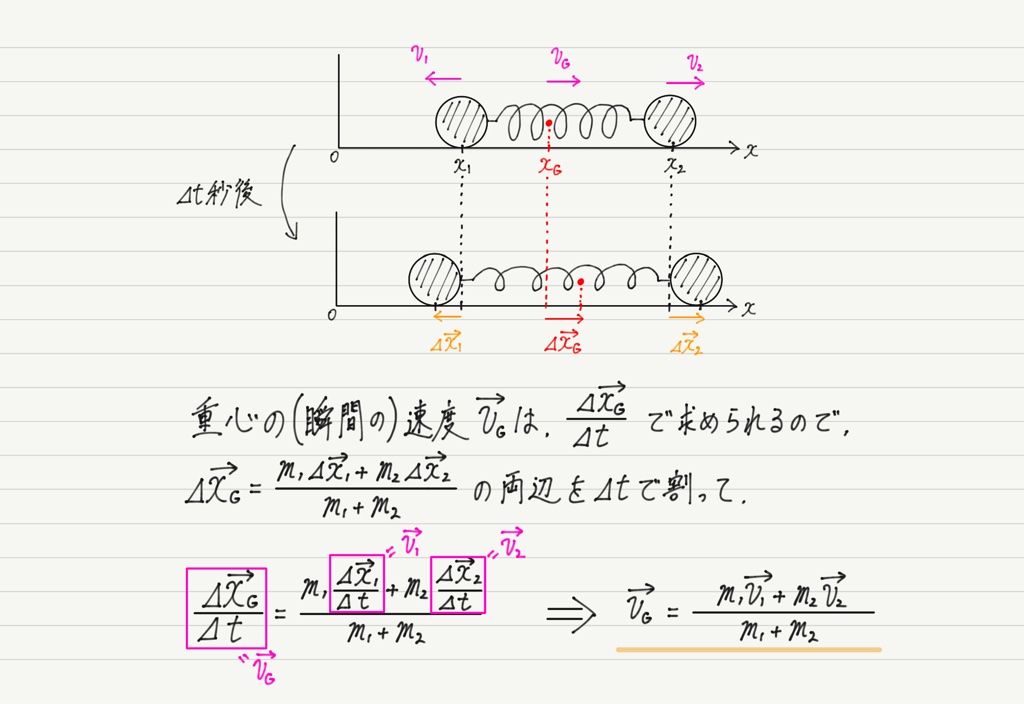
次に重心の(瞬間の)速度を求めてみます。
速度を求めるには変位をかかった時間で割ればOK!
これでvGを求めることができましたが,よく見るとこの式,けっこう面白いことになっています。
右辺の分子に注目してください! これって物体系全体の運動量ですよね!?
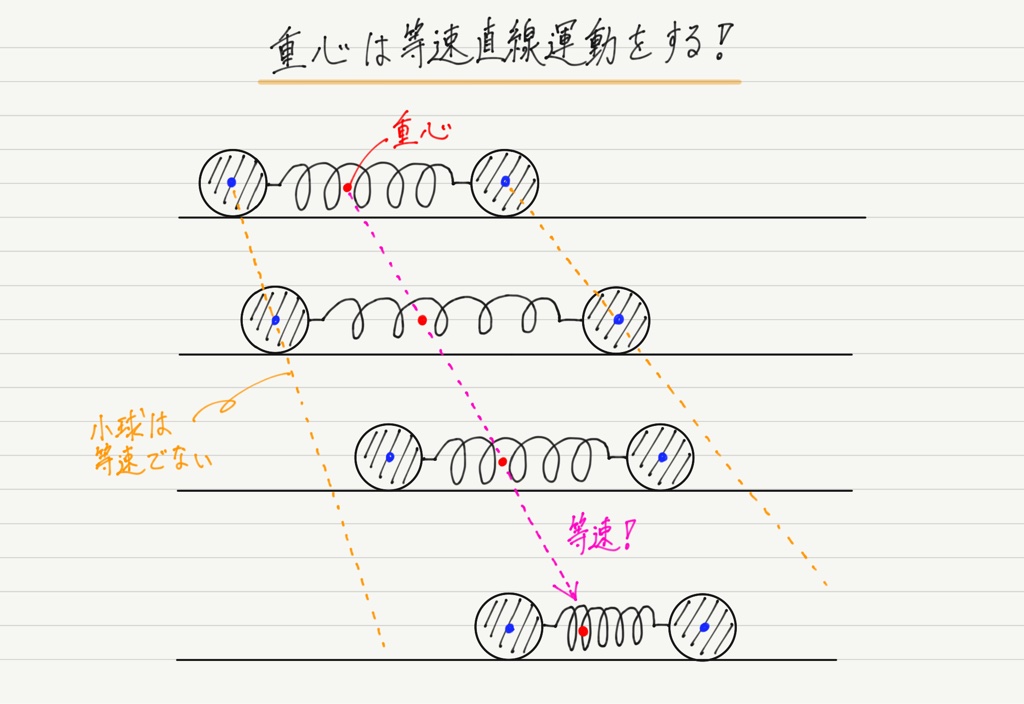
今回考えている「ばねにつながれた2物体からなる物体系」には外力がはたらいていない(=運動量保存則が成り立っている)ので,重心は等速直線運動をします!
一見複雑に見えるばねでつながれた2物体の運動も,やはり重心だけに注目すると非常に単純な運動だということがわかりました。
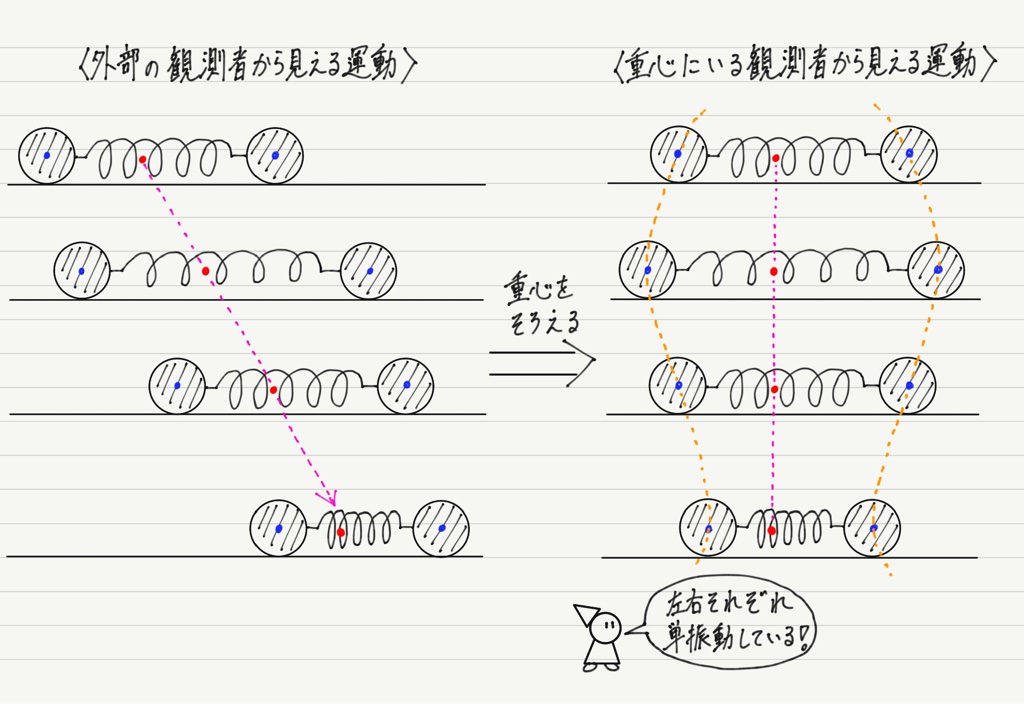
あとは重心以外の運動を調べればOK。 さっきと同様に重心に観測者を置いて考えましょう。
この観測者から見ると重心は止まって見えるので,重心の位置を固定してみます。
重心にいる観測者から見るとそれぞれの小球は単振動しているだけ!
これで重心は等速直線運動,各々の物体は単振動と,よく知っている運動に分けることができました!
ここまで来ればあとは計算でいろいろ求めることもできそうですが,具体的な計算はここでは割愛します(演習問題編で扱うのでそちらを参照)。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。