剛体の力学のラストを飾るのは「重心」のお話です。 重心という言葉自体はこれまでの記事にも何度か登場しているのですが,ここで改めて解説していこうと思います。
重心と重力
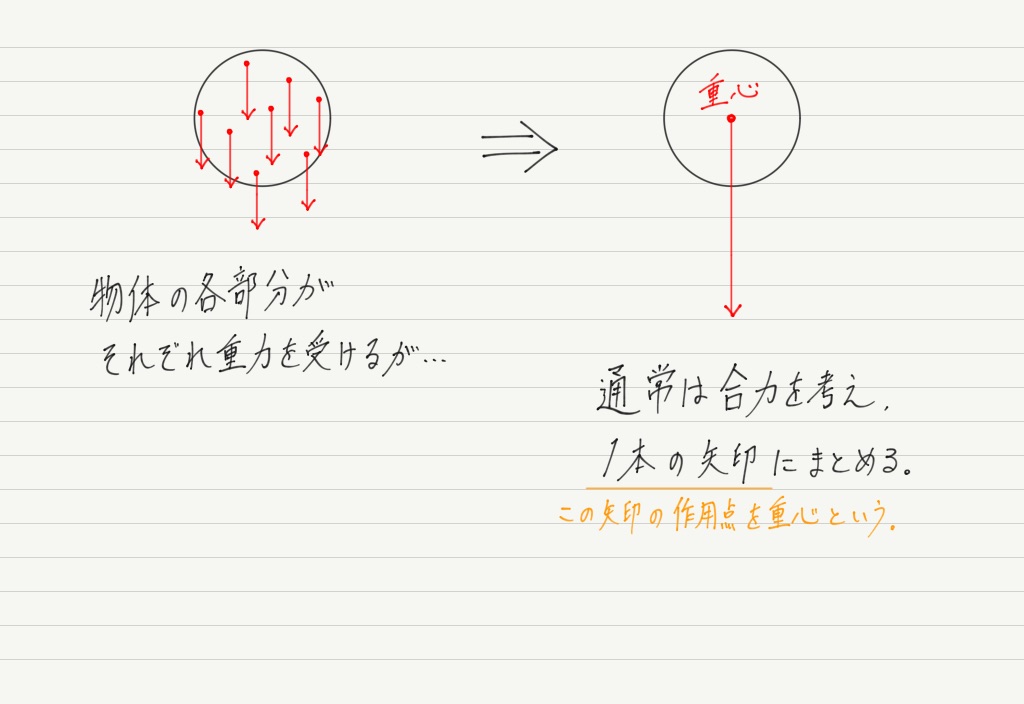
中学校の理科で「重力は物体の真ん中から矢印を書き始める」と教わりますが,大きさのある物体の場合,重力は物体の各部分にはたらきます。
ただ,それらをすべて書くのは面倒,というか不可能なので,それらの合力を考えて重力を1本の矢印で表しています。
重力を1本の矢印で書くということは,物体全体に質量が分布しているのではなく,「重心に,その物体のすべての質量が集まっている」と考えていることになります。
そう聞くと,「え?それって大丈夫なの?」と疑いたくなりますが,実際に大丈夫であることはニュートンによって証明されていますので,ご安心を。
あとで問題を解くときにこの考え方を使って解いていきます。
重心はどこにある?
では,その重心は具体的にどこにあるのでしょうか?
先ほど「物体の真ん中」という言い方をしましたが,物理の問題に登場するほとんどの物体の重心は真ん中です。
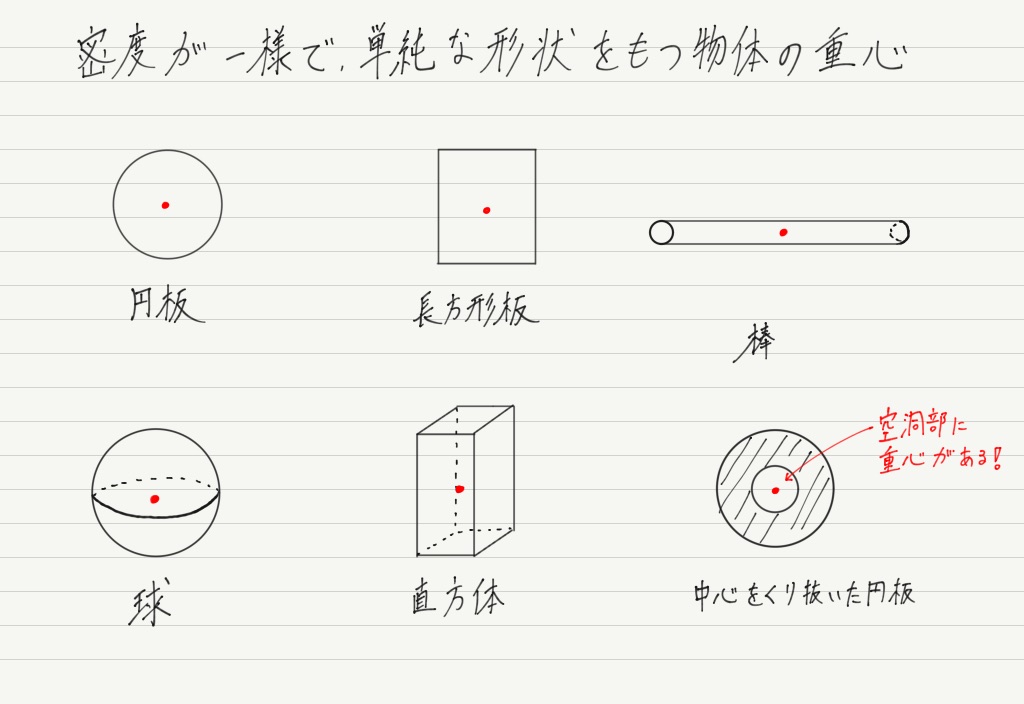
もう少し正確に表現すると,「円(球),棒,長方形(直方体)」の形をした,「密度にムラがない(“密度が一様”という)」物体ならば,重心は物体の真ん中にあります。
では,それ以外の場合,重心の位置をどのようにして特定すればいいでしょうか?
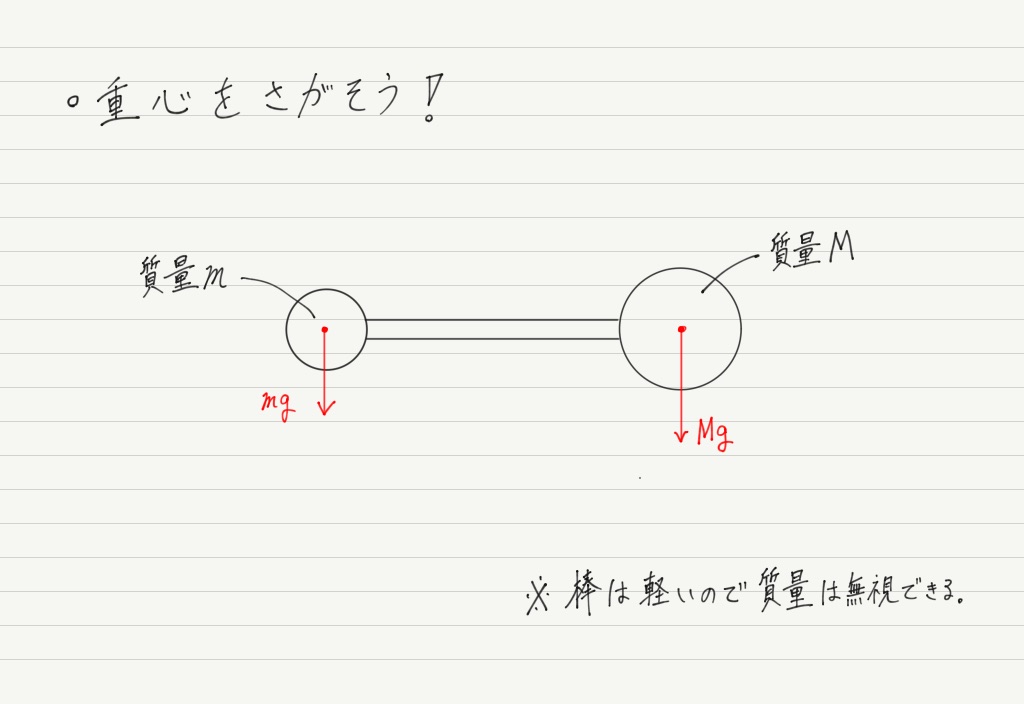
一番簡単な場合として,軽い棒の両端に質量の異なるおもりを取り付けた物体の重心を求めてみましょう。
「重心は重力の作用点」というのがポイントになります。
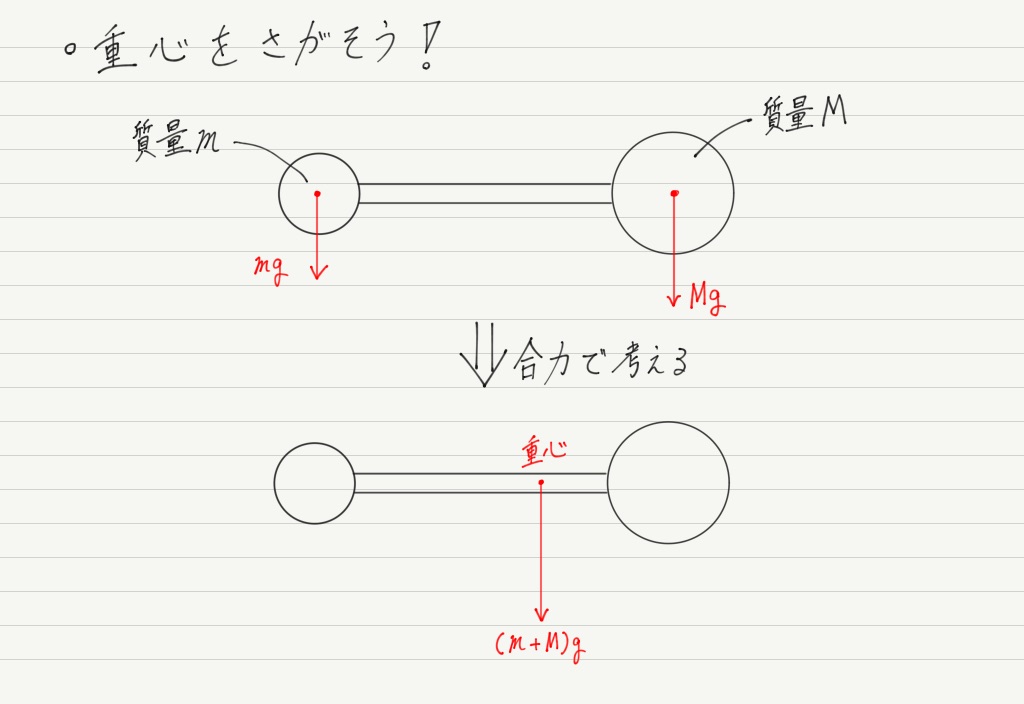
棒の両端のおもりにそれぞれ重力がはたらきますが,その合力がはたらく位置が全体の重心になります。
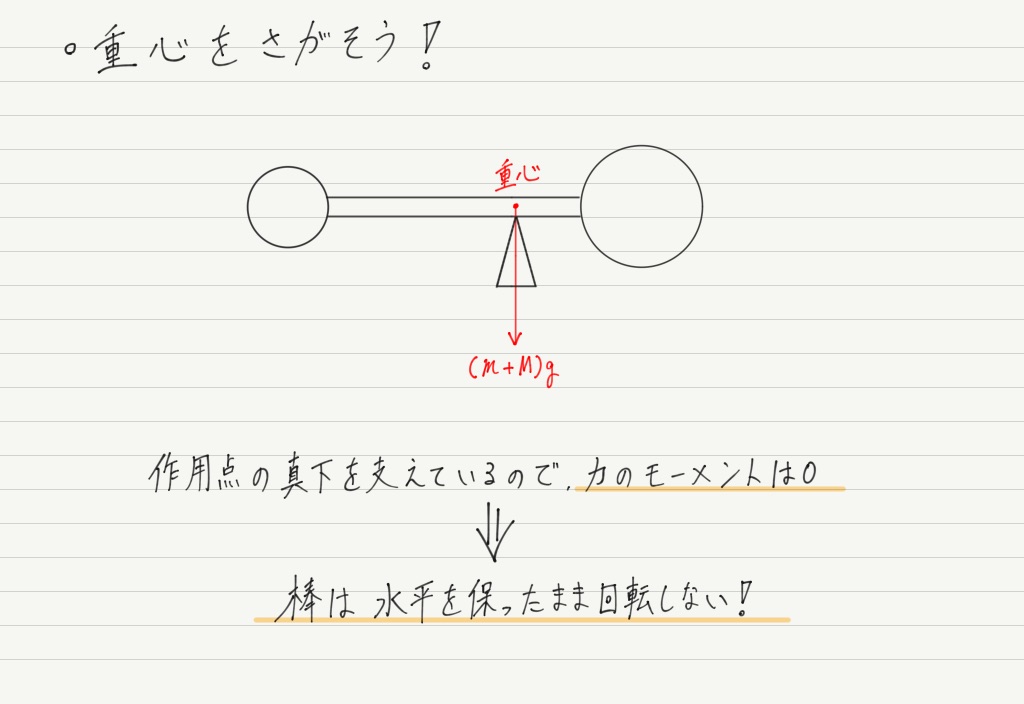
2つのおもりにはたらく重力をまとめて1つにしたら,今度はそこを支点にして棒全体を持ち上げてみましょう!
重心を支えると物体はバランスをとって倒れませんが,その理由がこれです!!
いよいよ重心の位置を計算していきますが,合力という見方をやめて,再び両端のおもりにはたらく重力で考えましょう。
見方を変えても現象は変わらないので,当然棒はバランスを保ったままです。
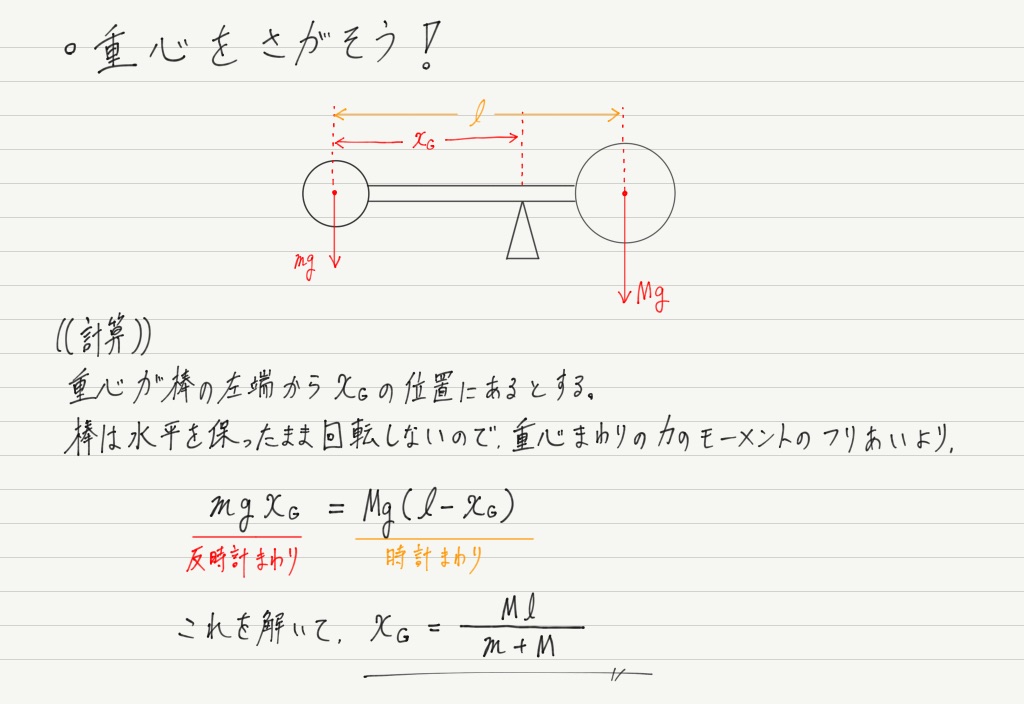
重心を支えると棒が傾かないということは,重心まわりの力のモーメントがつりあっているということを示しています!
(モーメントのつりあいがよくわからない人は前回の記事を参照してください。)
これで,重心の位置を求めることができました!
いまの例は棒だったのでx座標しか出てきませんでしたが,板などの場合はx座標とy座標に分けて,それぞれ計算することになります。
物体が2つだけじゃなく,もっとたくさんある場合はモーメントで解くのはちょっと大変です。
そこで,物体が複数ある場合にも使える重心の座標を求める公式を紹介しておきます!
使い方にコツがいる(?)ので,例題へGO!
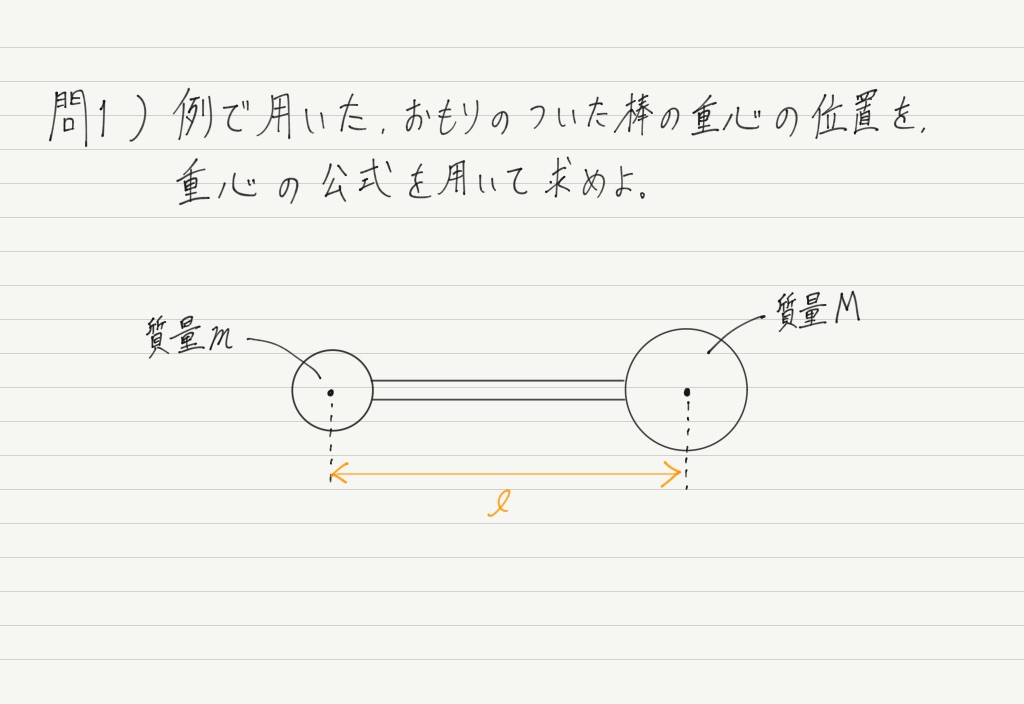
例題
では,例題いってみましょう!
もちろん答えは力のモーメントで解いたときと同じになるはずですが…
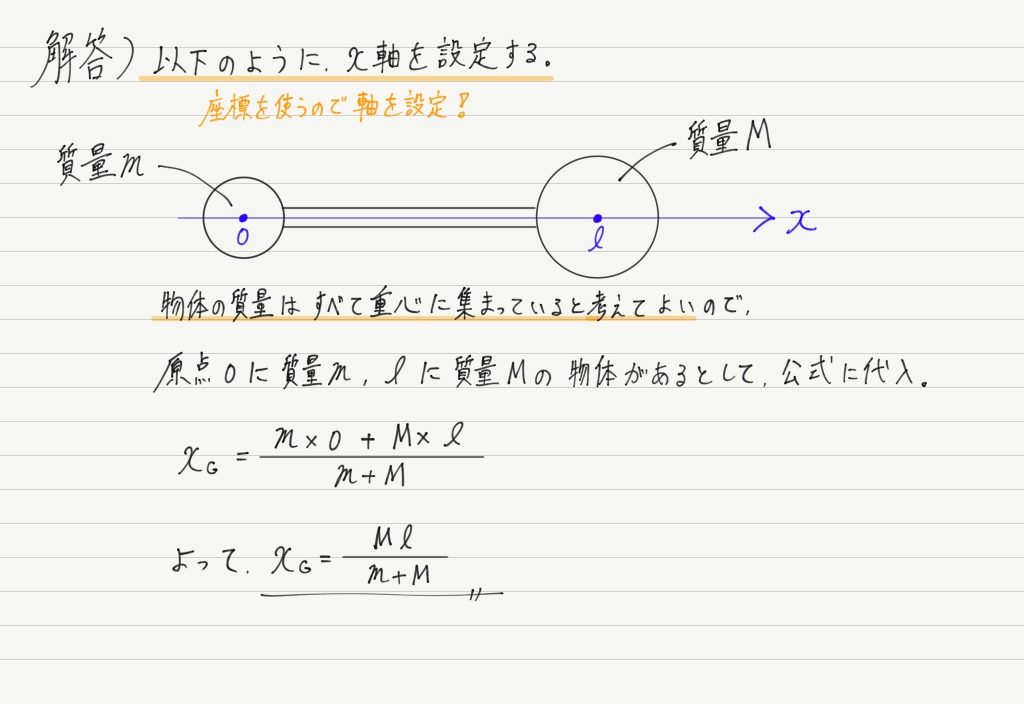
では解答です!
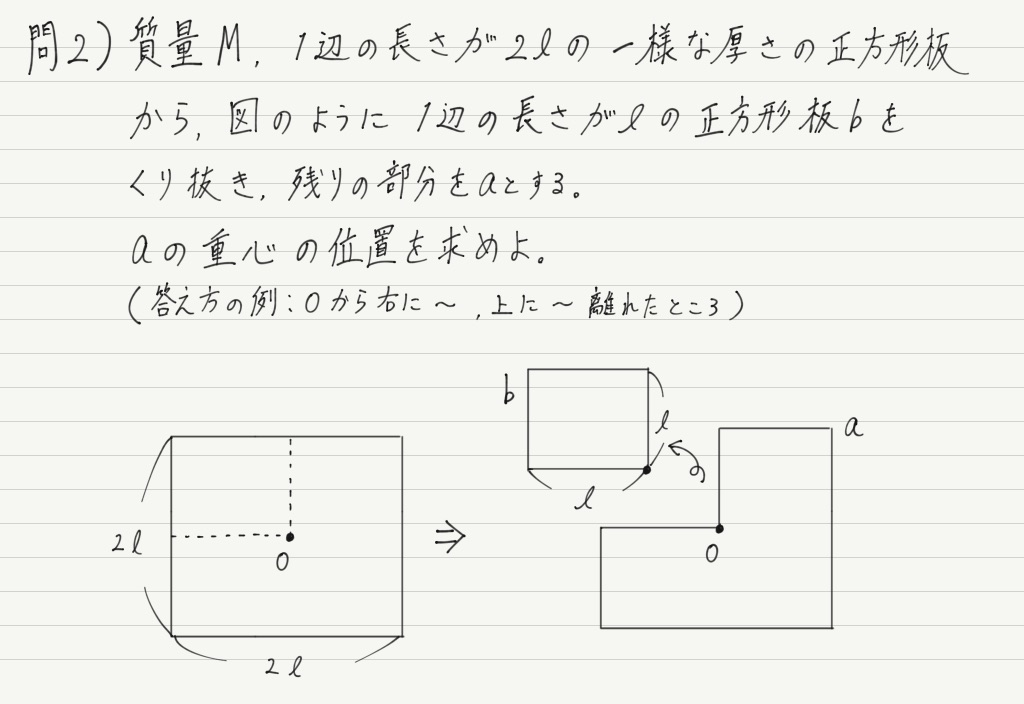
次はやや応用編。 物体の一部を取り除くタイプの問題です。
公式の中のxやyは,「距離」ではなく「座標」であることに注意して考えてください。
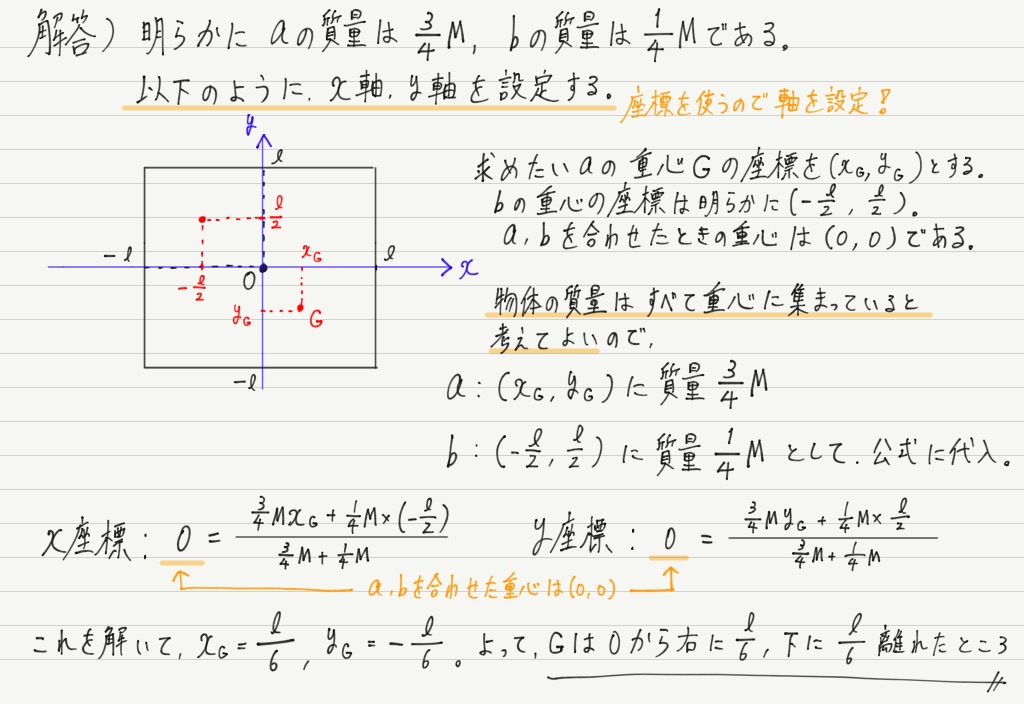
では,解答をどうぞ。
公式がわかっていても,一発で正解までたどり着けた人は少ないと思います。
自力で答えが出せるようになるまで,しっかり復習しておいてください。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
剛体の力学のお話はこれにておしまい。 次回からは再び質点の力学に戻ります。
いよいよ力学的エネルギーと双璧をなす概念,「運動量」の登場です!