質点にはたらく力が分かれば運動方程式を立てて運動の様子を調べることができたように,剛体では力のモーメントが分かれば,回転運動の様子を調べることができます。
…が,運動しているより,止まっている方が調べるのが簡単です。
そのため,物理基礎では運動方程式をやる前に,力のつりあいについて学習しました。
質点が動き出さない条件は,質点にはたらく力がつりあっていることです。
今回は「剛体が動き出さない条件」について考えてみましょう。
質点とのちがい
さて,剛体と質点で動き出さない条件にちがいはあるでしょうか?
質点と同様,はたらく力がつりあってさえいれば動き出さないような??
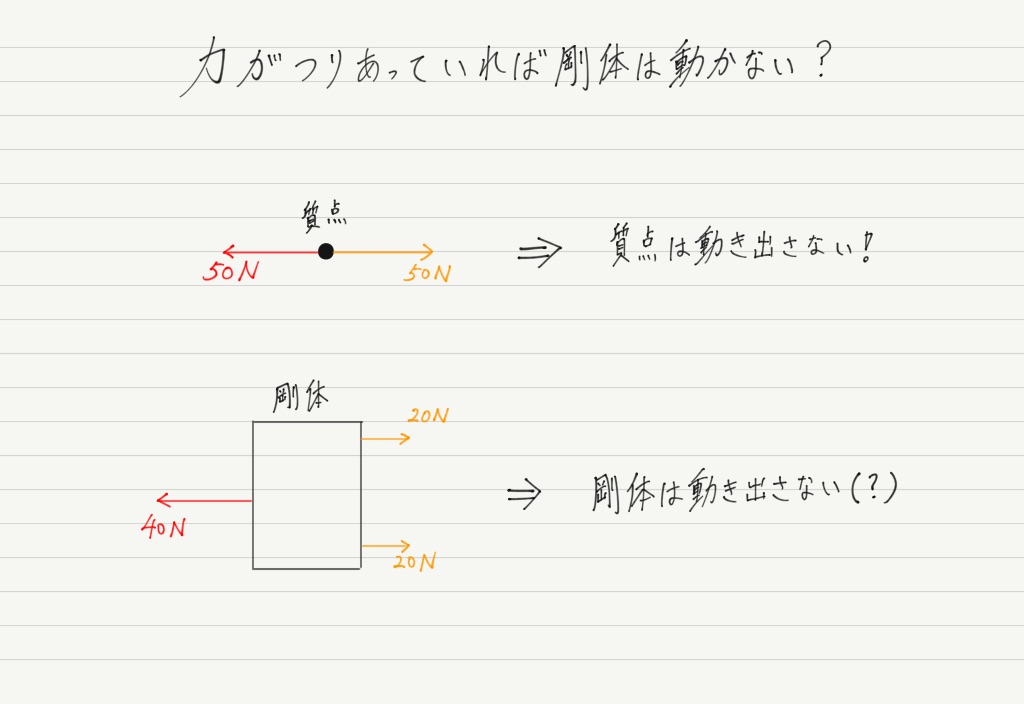
では,下の図を見てください。
右方向に引っ張る力が50N,左方向に引っ張る力も50Nなので,この剛体にはたらく力は確かにつりあっています。
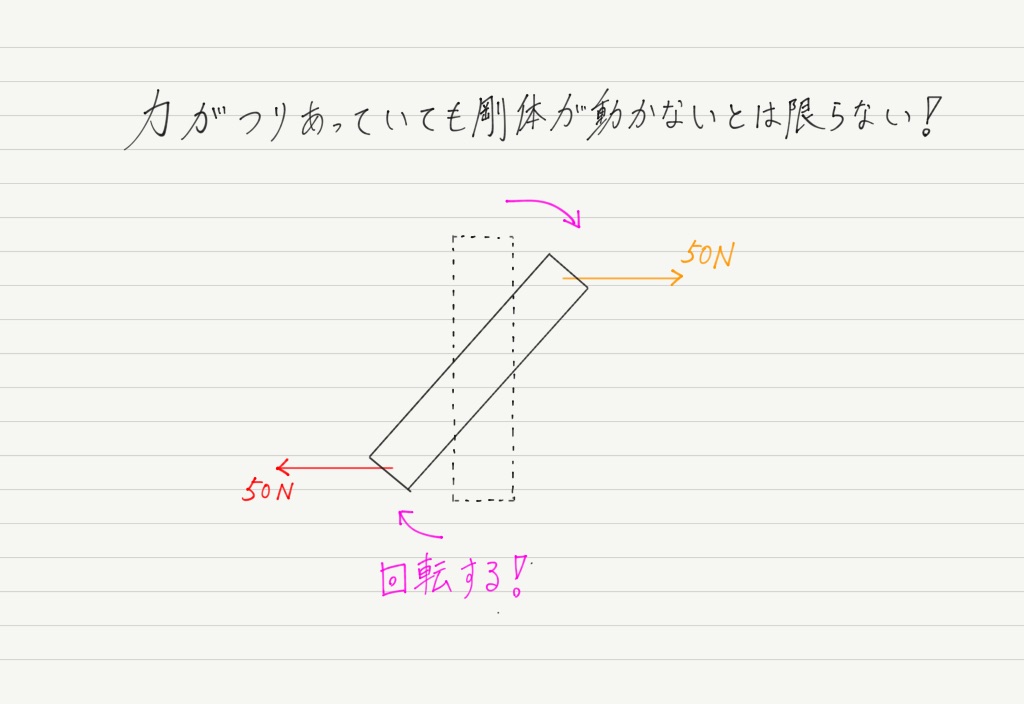
ところが,頭の中で想像すればわかるとおり,この状態だと剛体は動き出します!
そう! 回転し始めるのです!
剛体の運動は質点の運動に比べると複雑です。
それは,物体が向きを変えずにただ平行移動するだけの「並進運動」に加えて,上で見たような「回転運動」が加わるから。
(※ 質点は “点” なので回転するという概念がなく,並進運動しかしない)
なんだか難しそうな気配を醸し出していますが,果たして…?
2つのつりあい
剛体の運動は並進運動と回転運動の組み合わせで出来上がっているので調べるのは大変そうですが,そんなときはこの有名な言葉を思い出してください。
「困難は分割せよ」by デカルト
いろいろな要因が組み合わさると物事は複雑に見えますが,個々の要因自体は単純,というのはよくある話です。
剛体の運動もこれに当てはまります。
つまり,並進運動と回転運動を別々に捉えてしまえばよいのです!
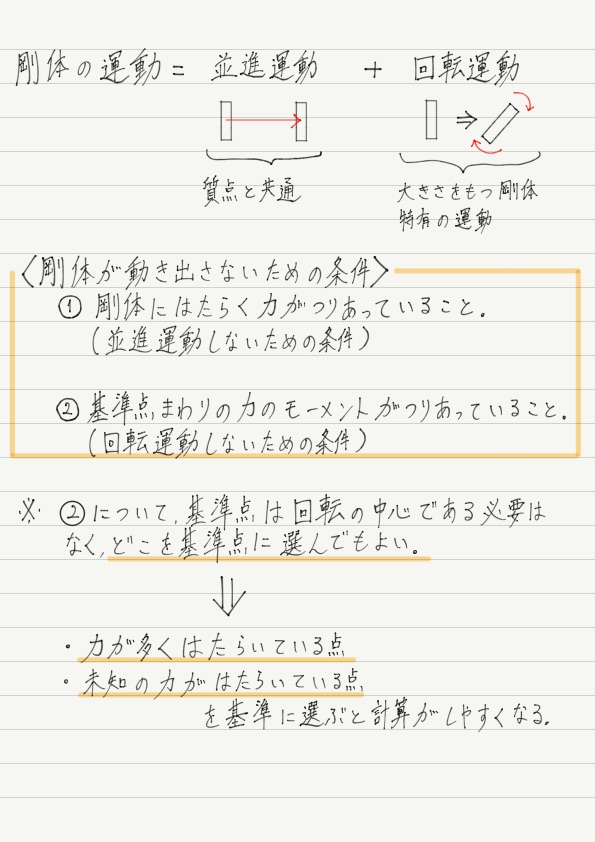
いま我々は剛体が動き出さない条件を考えたいわけですが,デカルトの言葉通り「剛体が動き出さない=剛体が並進運動せず,回転運動もしない」というふうに分割して考えます。
それぞれの条件を考えてみましょう。
まず,質点でやったとおり,「並進運動しない条件=力がつりあっていること」です。
物体が右に動き出すには,右向きの力の大きさが左向きの力の大きさを上回っていなければいけません。
これは質点に限らず,剛体でも同じことが言えるはずです。
次に回転しない条件ですが,回転の原因は何だったか思い出してください。
そう! 力のモーメントでしたよね!
では,剛体を時計まわりに回転させようとする力のモーメントと,反時計まわりに回転させようとする力のモーメントが同時に存在したらどうなるでしょう?
このように,逆方向のモーメントがある場合,大きさが大きい方に回転しようとします(当たり前!)。
言い換えると,時計まわりの力のモーメントと,反時計まわりの力のモーメントが同じ大きさ(この状態を「力のモーメントがつりあっている」という)ならば,剛体はどちらにも回転しないことになります!
よって,「回転運動しない条件=力のモーメントがつりあっていること」です。
「力のつりあい」と「力のモーメントのつりあい」,2つのつりあいの式が同時に成り立つことが,剛体が動き出さない条件になります!!
例題
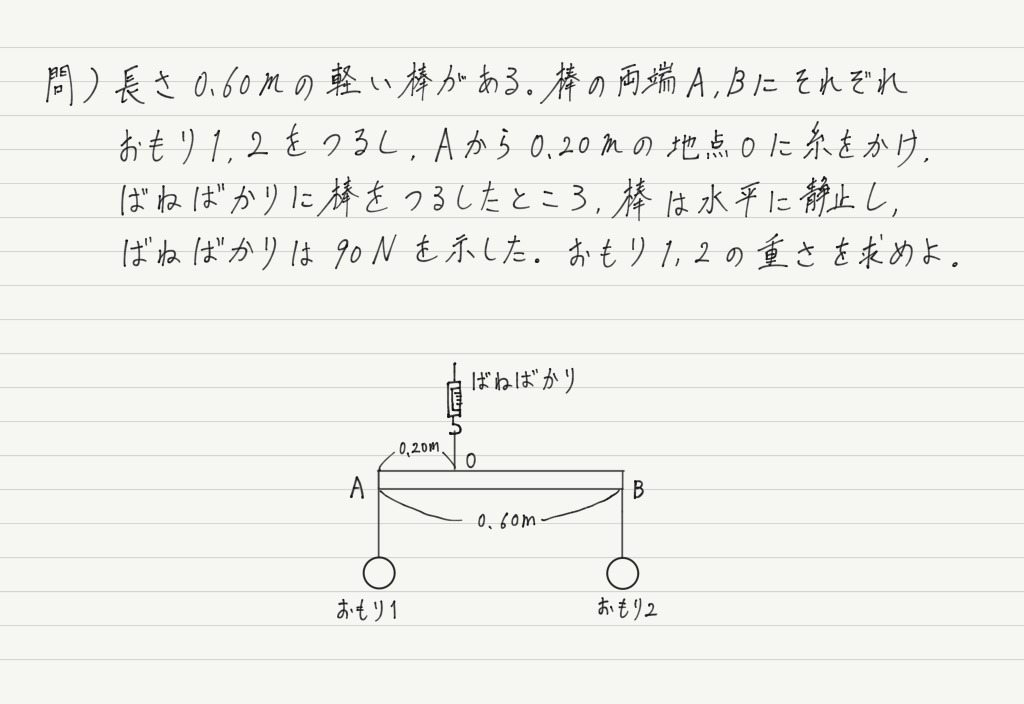
実際に問題を解いてみるのが一番手っ取り早いので,さっそくやってみましょう。
ここでいったん読むのををやめ,手を動かして解いてみてください。 答えはこのすぐ下です。
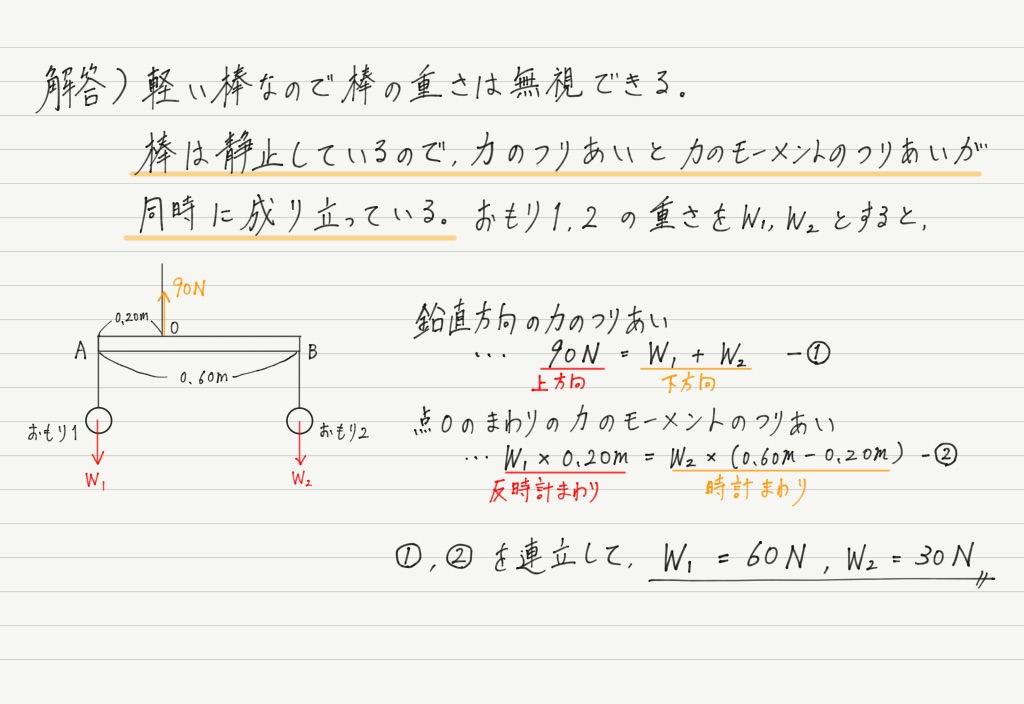
では,答え合わせしてみましょう!
力のモーメントのつりあいばかりに気を取られて,力のつりあいを忘れる人が結構多いので注意しましょう!
問題が解けたので一件落着ですが,もうひと踏ん張り。
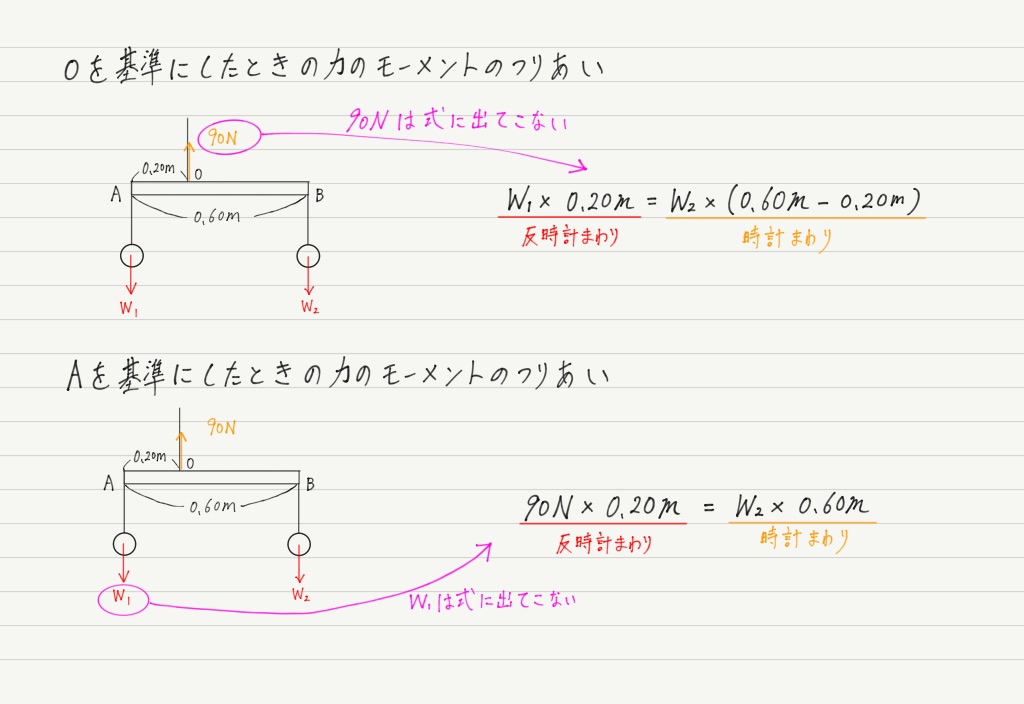
多くの人が上の解答のように,「点Oのまわりの力のモーメント」を考えたと思います。
では,点Aのまわりの力のモーメントで考えたらどうなるでしょうか?
なんと,これでも問題が解けてしまいました!!
今回の例題は2つのおもりのうち,どちらかの重さが少しでも変化すれば,棒は点Oを中心にどちらかに傾きます。
ですが,だからといって点Oをモーメントの基準にする必要はありません。
実際,点Aのまわりの力のモーメントを考えても問題を解くことができました。
なぜ回転の中心以外を基準にしても解けるのでしょうか?
それは,この問題では静止した剛体を扱っているから。
力のモーメントの基準を決めることは,「そこを中心に物体が回転すると仮定する」ことに等しいです。
ところがこの問題では剛体は静止しているので,どこを回転の中心だと仮定しても一向に構いません。
どうせ回転しないんだから。
よって,モーメントのつりあいを計算するときは,どこを基準にしてもよいという結論になるのです!
基準の決め方
モーメントの基準をどこにとってもいいのであれば,なるべく計算が簡単になるように選びたいですよね!
時間も短縮できるし,何より計算ミスのリスクが減ります。
基準の選び方のポイントは,「基準にはたらく力は,力のモーメントのつりあいに含まれない」ということです。
先ほどの例題で確認してみましょう。
基準にはたらく力は,剛体を回転させるはたらきをもたない(=力のモーメントが0)ので,モーメントの式に出てこないのです(シーソーの支点をいくら押しても,シーソーが動かないのと同じこと!)。
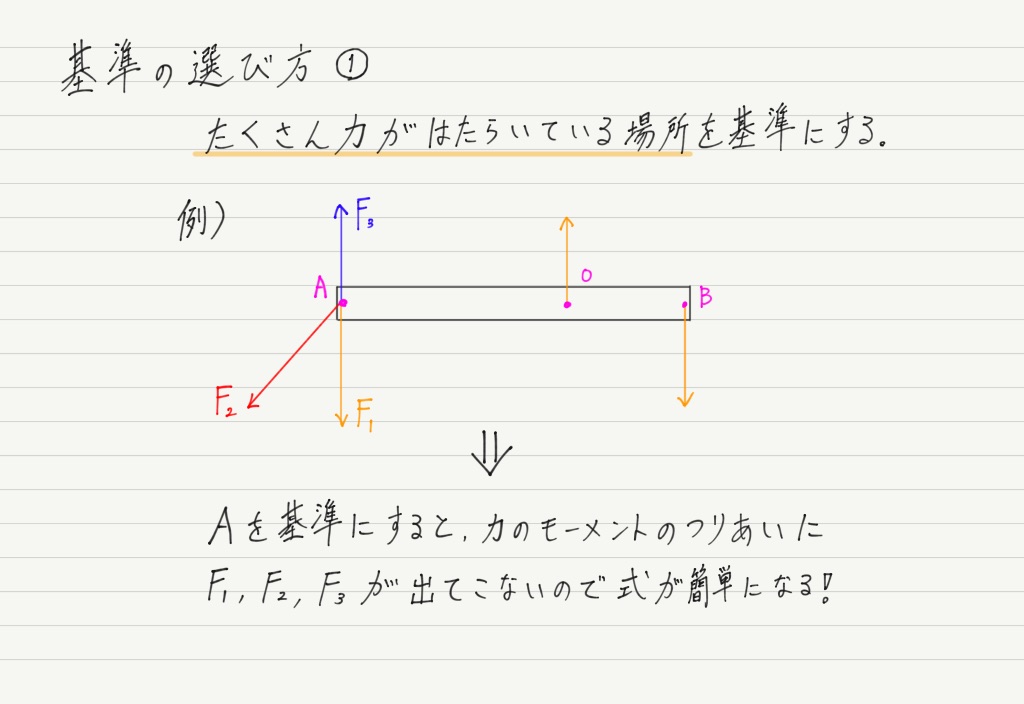
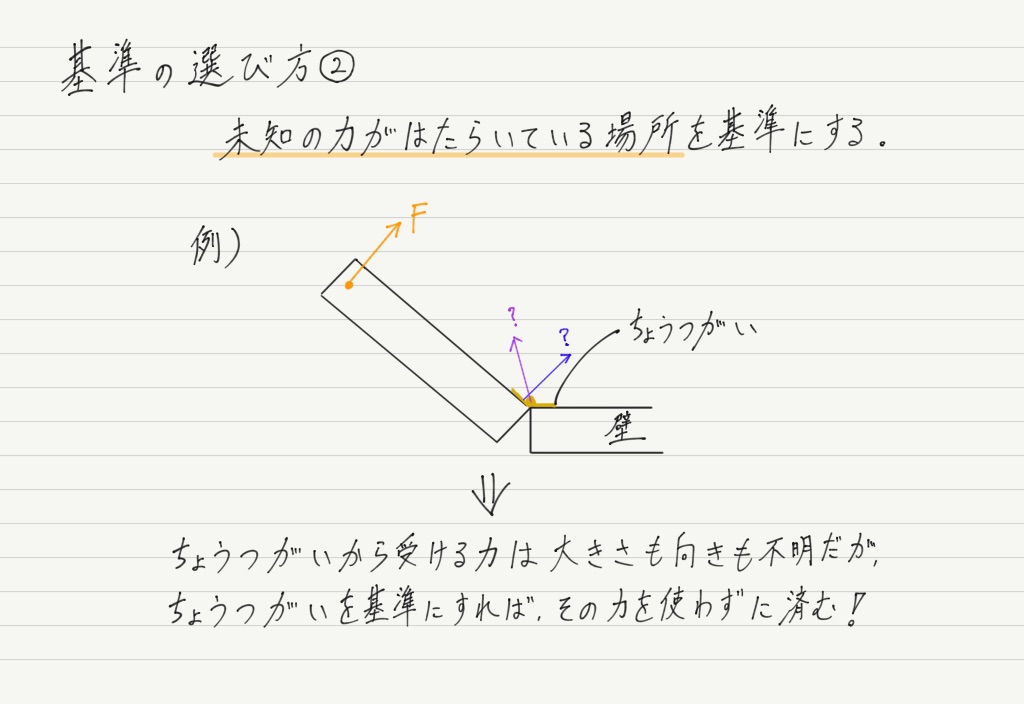
これらのことを踏まえて,具体的な選び方を伝授します。
問題文に指定がなければ,この方針に沿って基準を決めましょう!
今回のまとめノート
補足:一番最初に例に挙げたような,平行で逆向き,同じ大きさの2力を「偶力」といいます。
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
今回「剛体が動き出さない条件」をやったから,次回はいよいよ回転運動だと思うじゃないですか!?
ところが残念!! 高校物理では「動かない剛体」しか扱いません。
回転運動は大学でのお楽しみということにして,次回は剛体の力学の締めとして「重心」に関する話題です!