今回は光の反射・屈折の話題でよく問われる「全反射」という現象について解説していきます。
前回の記事の補足のような感じですので,前回の記事を未読の方はまずそちらをどうぞ。
全反射とは何か
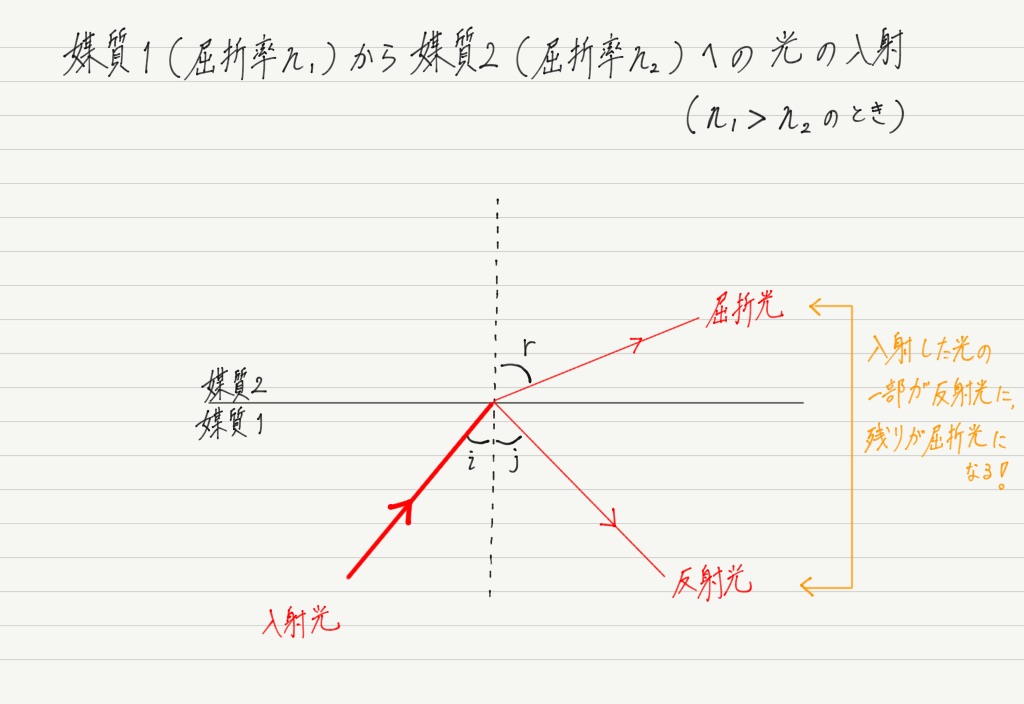
屈折率の異なる物質に光を入射したとき,その境界面で,光の一部は反射し,残りは屈折します。
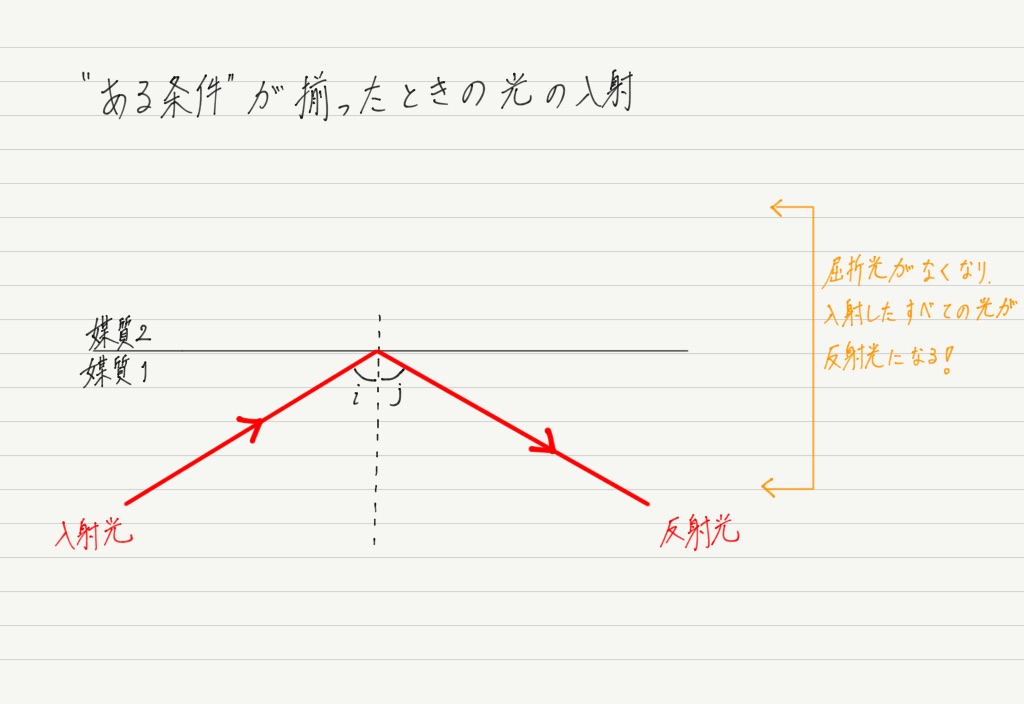
ところが,“ある条件” が揃うと屈折光がなくなり,すべて反射してしまいます。
これが全反射と呼ばれる現象です。
屈折しないで全部反射するから “全”反射。 そのまんまのネーミングでわかりやすいですね笑
全反射が起こる原理
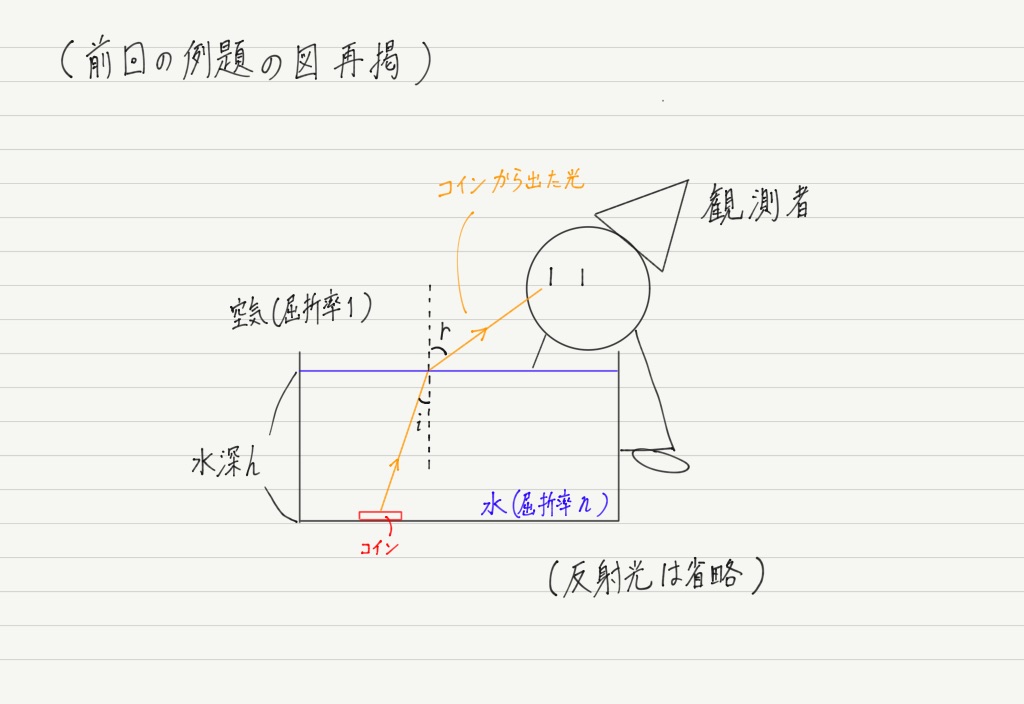
水中のコインを上から覗く,という前回の例題の設定を思い出してください。
観測者がコインに近い場所にいる場合,コインは実際の位置よりも浅いところにあるように見える,という問題でした。
ところが,観測者が水槽から徐々に離れていくと,ある地点でコインが見えなくなります。
(※水槽のフチが邪魔になって見えない,という話ではありません。念のため。)
なぜ急にこんな話を持ち出したかというと,この現象の原因が全反射だからです。
順を追ってみていくと,
観測者が離れることで “ある条件”が揃う
→コインから出た光が全反射する
→屈折光がなくなるので,光が観測者の目に届かない
→コインが見えない
という理屈です。
では,そろそろ全反射が起こるための “ある条件” を解明していきましょう!
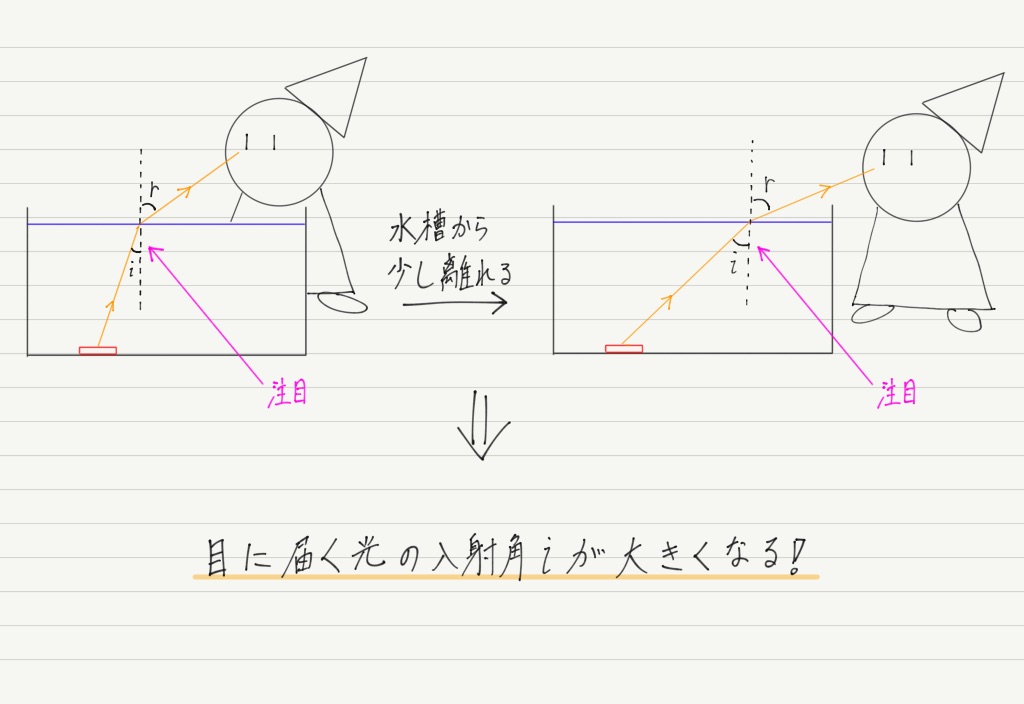
観測者が水槽から遠ざかるときに何が起こるか。
それは,コインから出て目に向かう光の入射角の変化です。
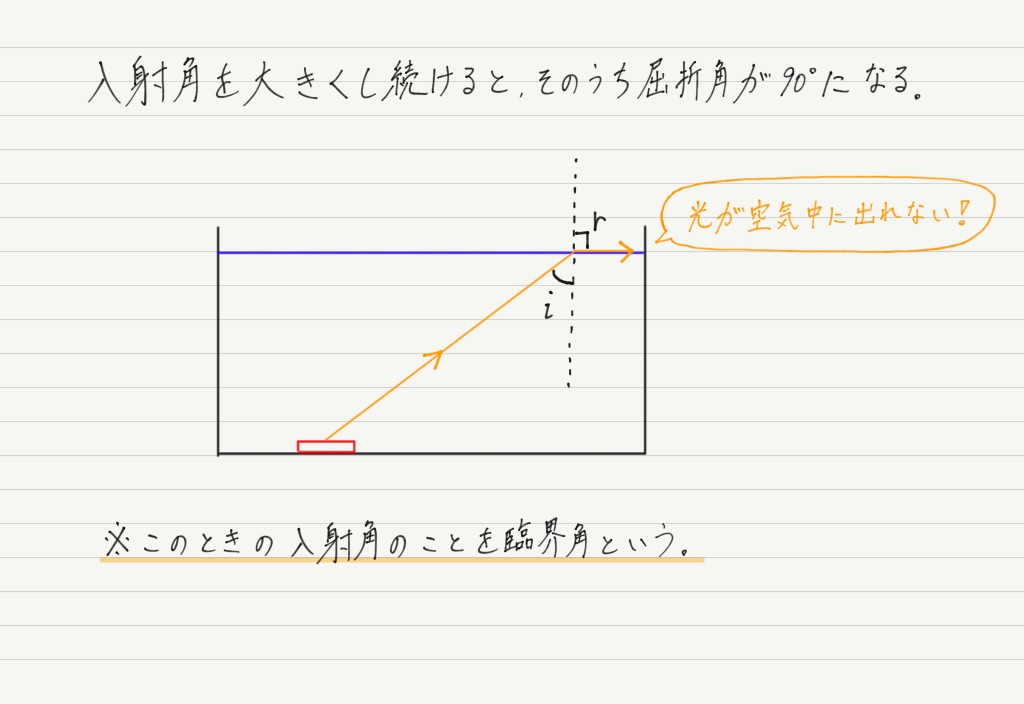
下図のとおり,水槽から離れれば離れるほど,入射角は大きくなっていきます。
入射角が変化すれば,それに伴って屈折角も変化しますが,そこが今回の最大のポイント!!
屈折率が大きい物質から小さい物質へ光を入射させる場合,入射角より屈折角のほうが必ず大きくなります。
このことを頭に入れた上で,先ほどの話をもう一度考えてみましょう。
観測者が水槽から離れることで,光の入射角が大きくなる。
→それに伴って屈折角も大きくなる。
→どこかのタイミングで屈折角が90°になる!!
屈折角が90°ということは,光は屈折して水面を進みます。
その結果,屈折光は空気中に出ることができず,目に届かなくなります。
要するに,臨界角とは屈折が起こるギリギリの入射角のこと。
なので,入射角が臨界角を超えると,屈折そのものが起こらなくなります。
全反射が起こる条件
話をまとめると,全反射が起こるための条件は,
① 屈折率が大きい物質から小さい物質に向かって光が入射していること。
② 入射角が臨界角を超えていること。
の2点です。
残る問題は,臨界角って具体的にどれぐらいなの?ってこと。 さっそく計算で求めてみましょう。
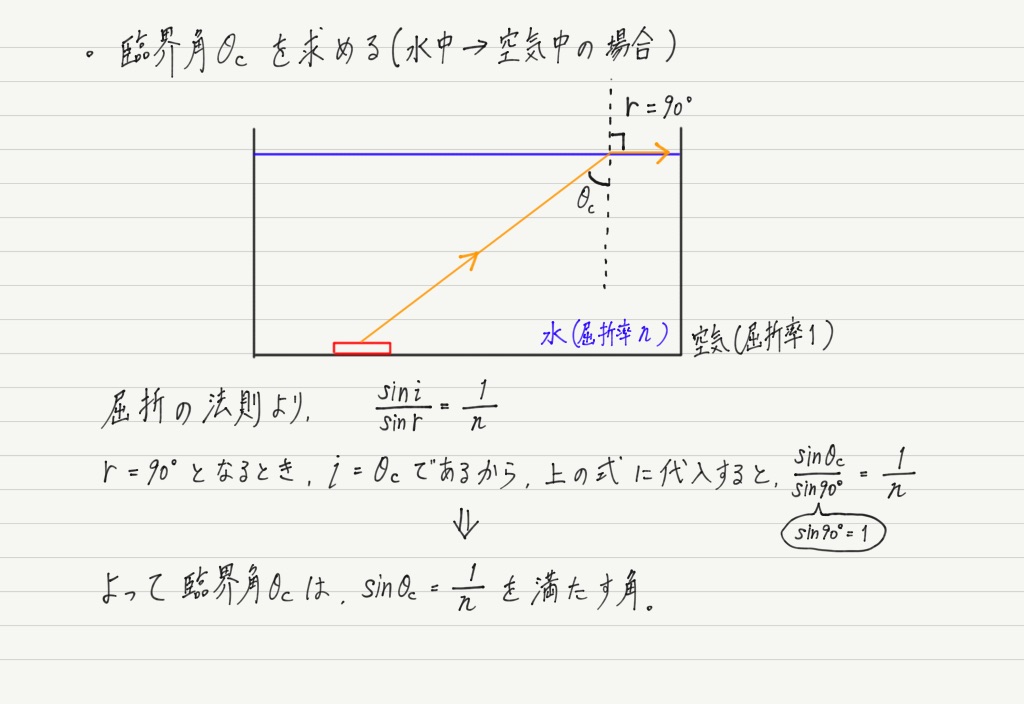
「臨界角=屈折角が90°になるときの入射角」のことなので,屈折の法則を適用してみると…
教科書や問題集でよく見る式が出てきました!
これを「全反射の式」とか言って暗記している人がいますが,それはナンセンス。
いま見たとおり,これは屈折の法則に r=90°を代入しただけ。
全反射の原理をしっかり理解していれば(仮にど忘れしても),自分で導けるはずです。
「全反射の式,ど忘れして問題解けなかったぁー」とかありえないからね!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は身近に利用されている光の屈折の例として,レンズについて学んでいきましょう!