以前,反射の法則・屈折の法則の説明はしていますが,ここでは光に限定してもう一度詳しく見ていきたいと思います(反射と屈折は高校物理では光に関して問われることが多い!)。
反射と屈折の法則があやふやな人は,まず復習してください!
問題ない人は先に進みましょう!
入射した光の挙動
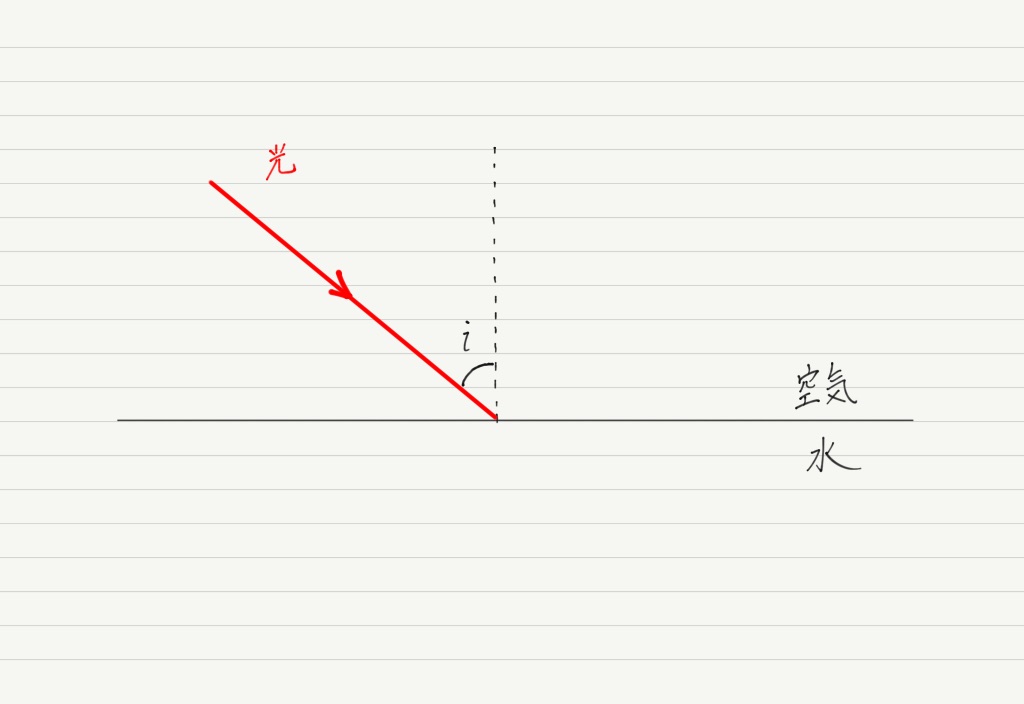
ではさっそく,媒質1(空気)から媒質2(水)に向かって光を入射してみます(入射角i)。
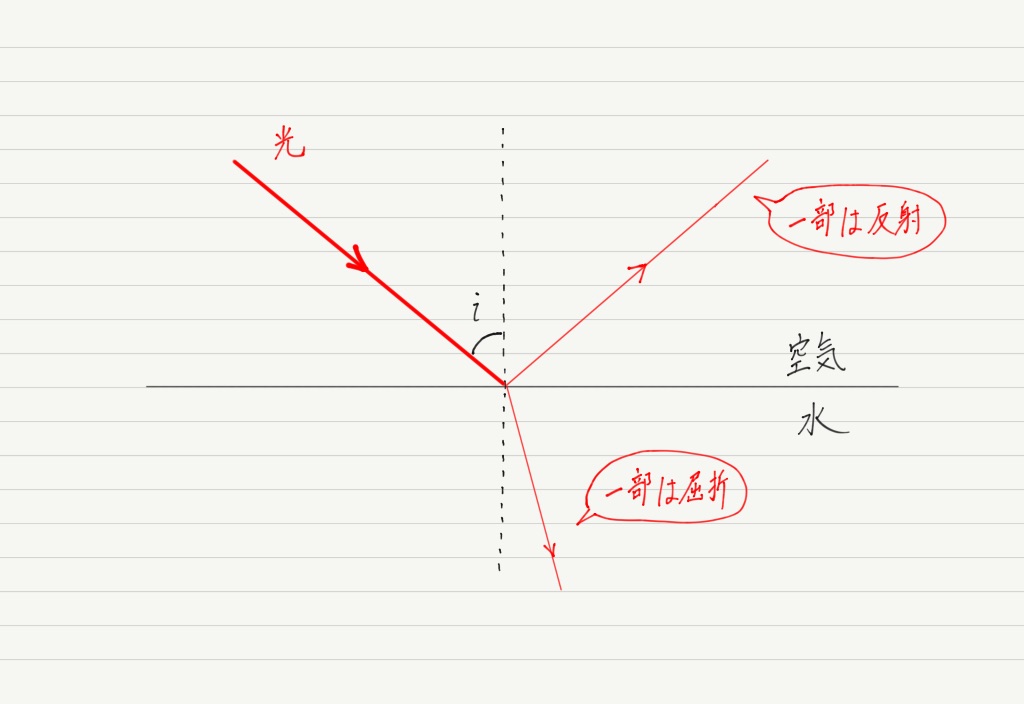
このとき光はどのように進むでしょうか? 屈折する? それとも反射?
答えは,「両方起こる」です!
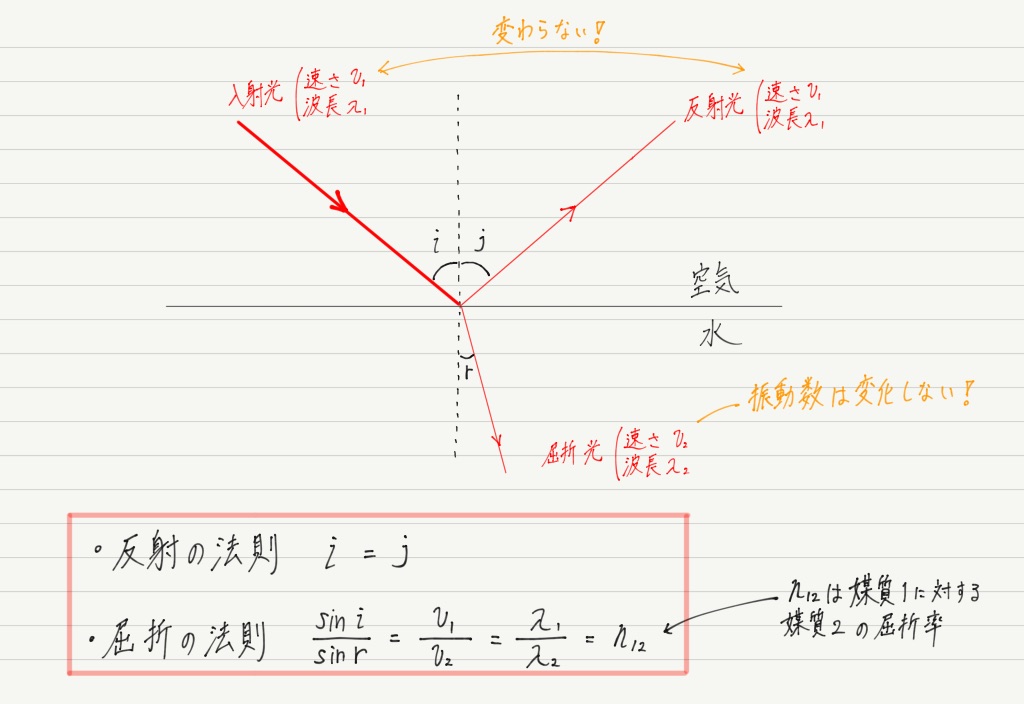
また,光も波の一種(かなり特殊ではあるけれど)なので,他の波と同様に反射の法則と屈折の法則に従います。
ここまでは特に目新しい話はナシ笑
絶対屈折率と相対屈折率
さて,屈折の法則の中には,媒質1に対する媒質2の屈折率,通称「相対屈折率」が含まれています。
“相対”屈折率があるのなら,“絶対”屈折率もあるのかな?と思った人は正解。
光に関する考察をするとき,真空中を進む光を基準にすることが多いですが,屈折率もその例に漏れません。
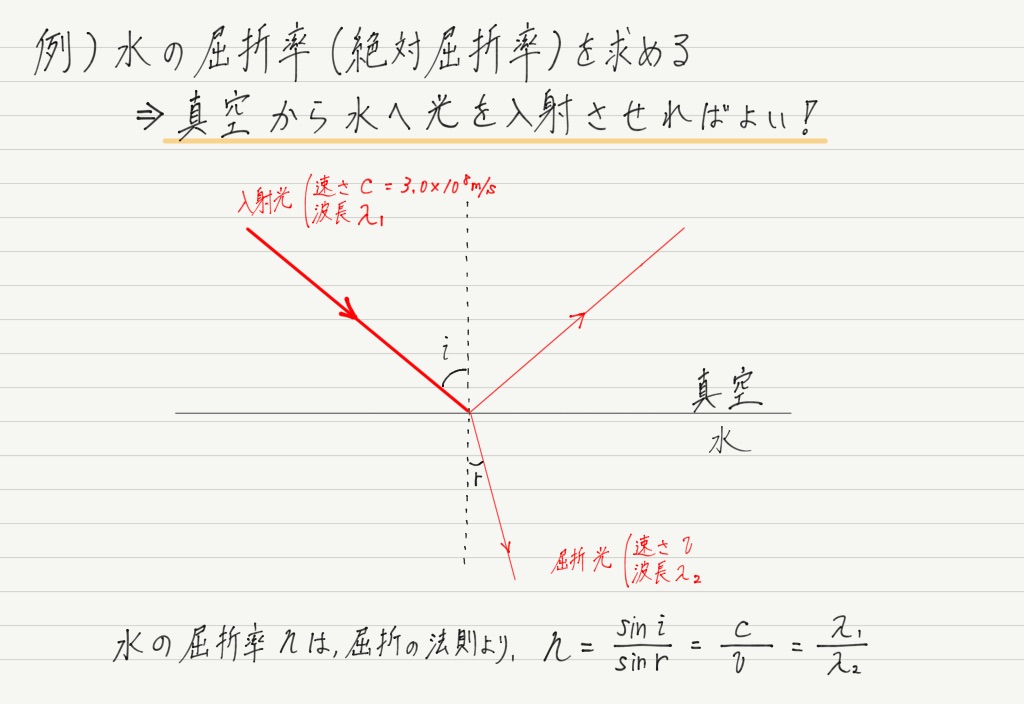
すなわち,真空に対する媒質の屈折率のことを「絶対屈折率」といいます。
相対屈折率は「水に対するガラスの屈折率」のように入射側と屈折側の2つの媒質がないと求められないのに対し,絶対屈折率は媒質単独で求めることが可能。
例えば,「水の屈折率」というような感じです。
媒質の絶対屈折率がわかれば,そこから相対屈折率を求めることも可能です!
この関係を利用して,以前やった屈折の法則を,絶対屈折率を用いた形に書き換えてみましょう!
問題集を見ると気づくと思いますが,屈折の問題はそのほとんどが光の屈折です。
そして,光の屈折では絶対屈折率を用いて計算することがほとんどです。
つまり,出番が多いのは圧倒的に絶対屈折率ver.になります!!
ではここで簡単な問題。
問:絶対屈折率ver.のほうが大事なのに,なぜ以前の記事で相対屈折率ver.を先にやったのか。
そしてその記事ではなぜ絶対屈折率に触れなかったのか。その理由を考えよ。
そんなの書いた本人にしかわからないだろ!なんて言わないでください笑
これまでの話が理解できていればわかるはず。
答えはこのすぐ下にありますが,スクロールする前にぜひ自分で考えてみてください。
答えは,「光以外の波は真空中を伝わることができない(必ず媒質が必要)から」です!
真空を伝わらないので,そもそも絶対屈折率を求めること自体不可能。
「真空を基準にする」というのは媒質を必要としない光だからこそできる芸当なので,光の分野じゃないと絶対屈折率は説明できないのです。
例題 〜ものの見え方〜
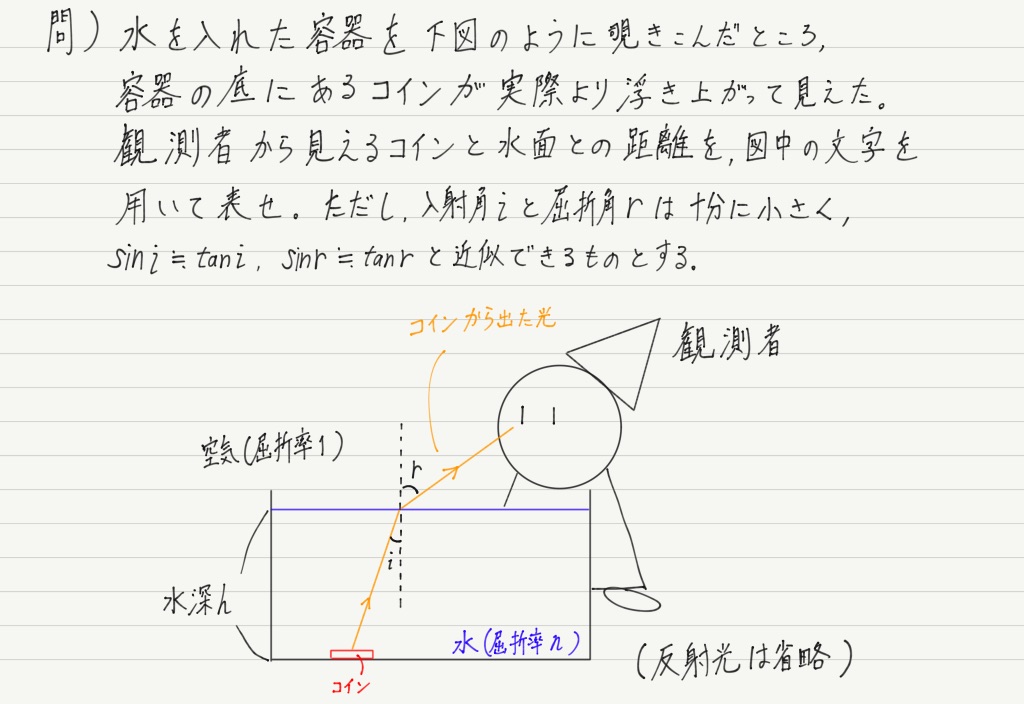
ひとつ例題をやっておきましょう。
(コインから出た光は水面で一部屈折,一部反射しますが,上の図のように普通は反射光は省略する。)
これはよく見るタイプの問題ですが, 屈折の法則だけでなく,「ものの見え方」について理解していないと解くのは難しいと思います。
というわけで,まずは屈折と見え方の関係について確認しておきましょう。
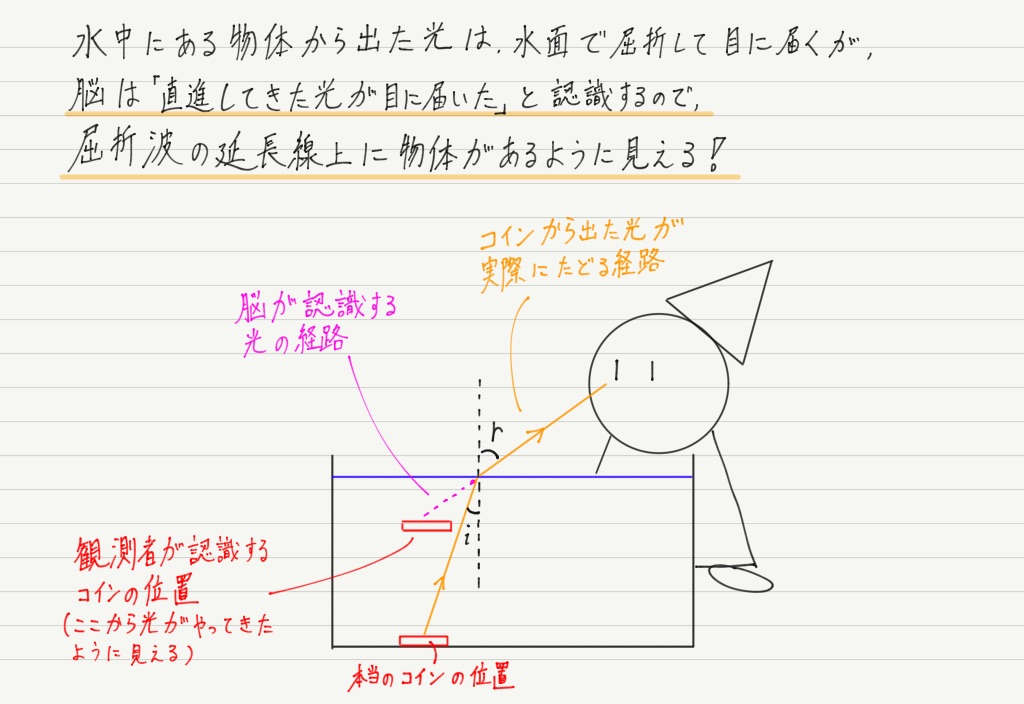
物質から出た光(物質で反射した光)が目に入ることで,我々は「そこに物質がある」と認識します。
肝心なのは,脳は「光は直進するもの」と思いこんでいることです!
これを踏まえた上で,先ほどの例題を考えてみてください。 答えはこの下に載せておきます。
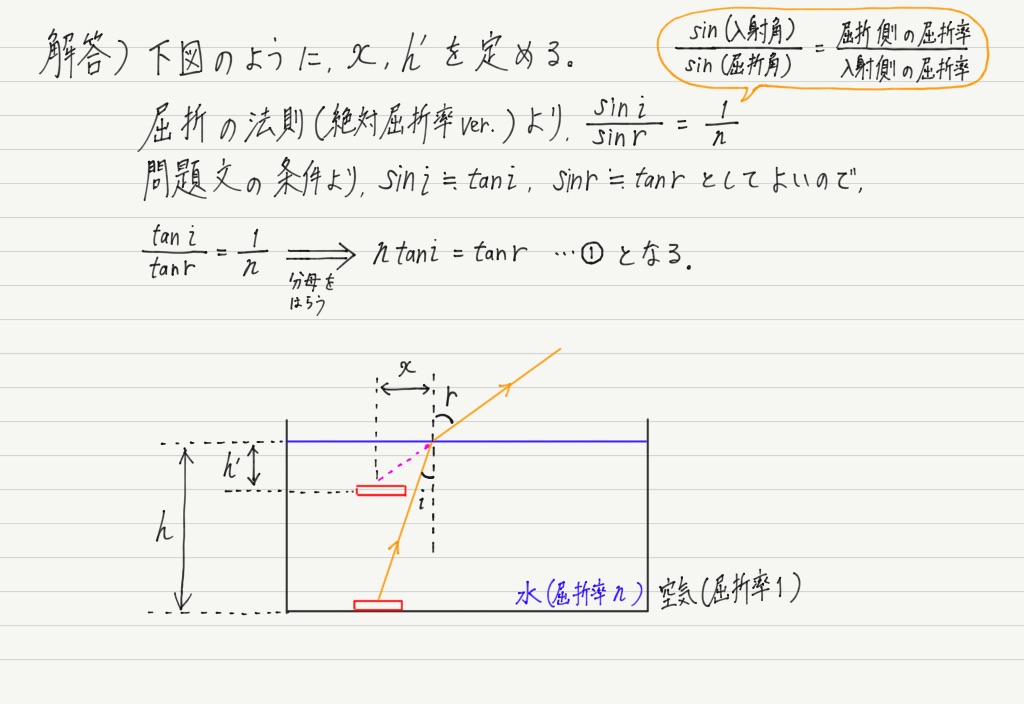
では解答を確認してみましょう。
近似式の扱いにも徐々に慣れていきましょうね!
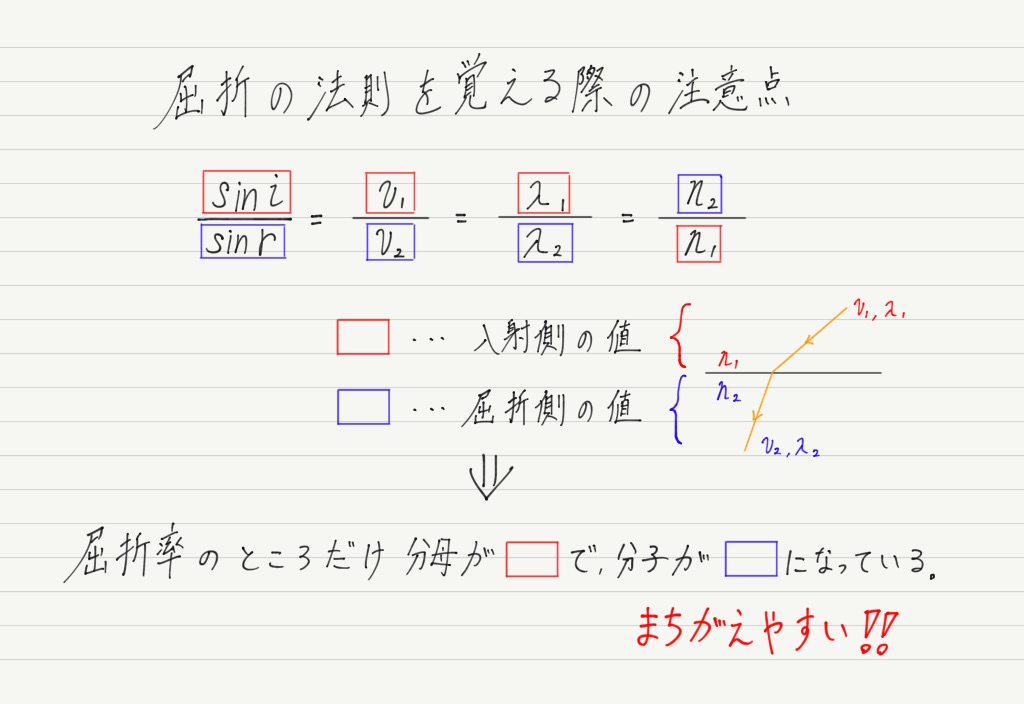
おまけ 〜屈折の法則の覚え方〜
個人的にですが,教科書に書いてあるこの屈折の法則(絶対屈折率ver.)って,ちょっと覚えにくいと思うんですよね…
屈折の法則の表記には改善の余地があると思っています。
具体的には,
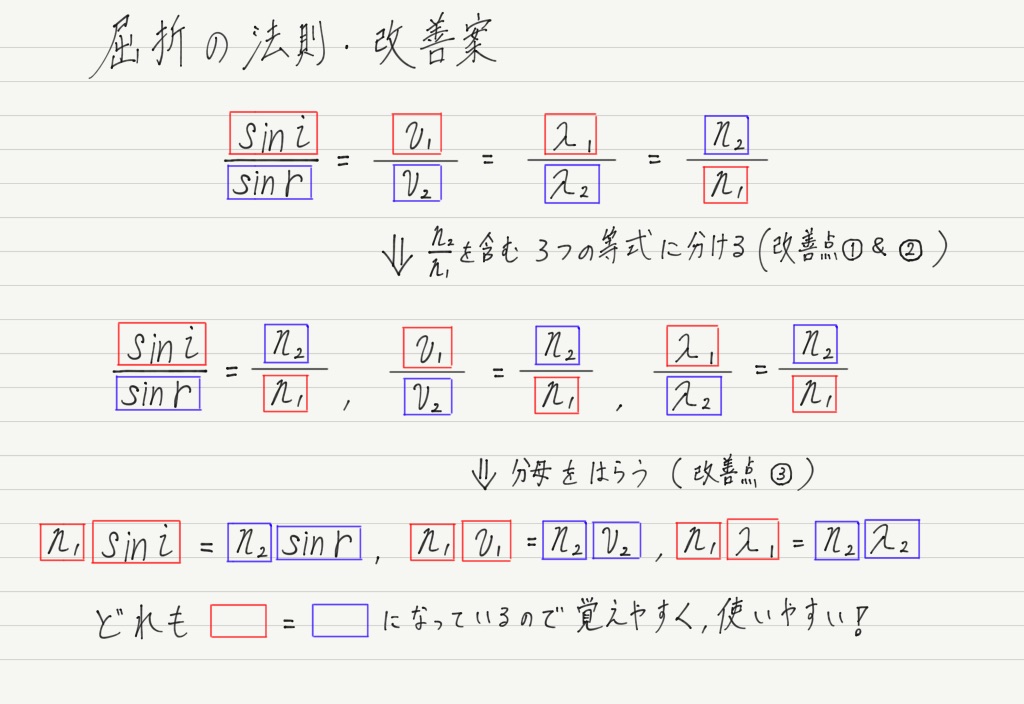
改善点①:計算するときは4つある分数のうち2つを選んで◯=△という形で使うので,4つの分数すべてをイコールでつなぐ必要はない。
改善点②:4つある分数の出番は対等ではなく,実際に問題を解くときは屈折率の出番が多い。
改善点③:計算するとき分母をはらうので,そもそも分数の形にしておく意味がない。
の3つです。
それを踏まえて,こんなふうに式変形した形で覚えるのはどうでしょうか?
このほうが覚えやすいし,実際使いやすいので,この形で覚えておくことを強くオススメします!
最後にひとつだけ注意事項があります。
今回の記事では絶対屈折率の考え方を強調したかったので,毎回「“絶対” 屈折率」と書いていましたが,
いちいち “絶対” と書くのは面倒なので普通は省略されます。
教科書や問題集で,単に「屈折率」と書いてある場合は絶対屈折率のことを指すと解釈してください。
私も今後は「屈折率」とだけ書くことが増えると思います。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は全反射という現象について詳しく解説していきます!
今回の内容と密接に関連しているので,よく復習しておいてください。