物理【波】第9講『全反射』の講義内容に関連する演習問題です。 講義編を未読の方は問題を解く前にご一読ください。
全反射屈折率の異なる物質に光を入射すると，境界面で一部反射して残りは屈折しますが，“ある条件” が揃うと屈折光がなくなり，すべて反射します。その条件を探ってみましょう。...
問題
[Level.1]
屈折率が3.0の物質Aから屈折率が1.5の物質Bに光を入射させたときの臨界角を求めよ。
[Level.2]
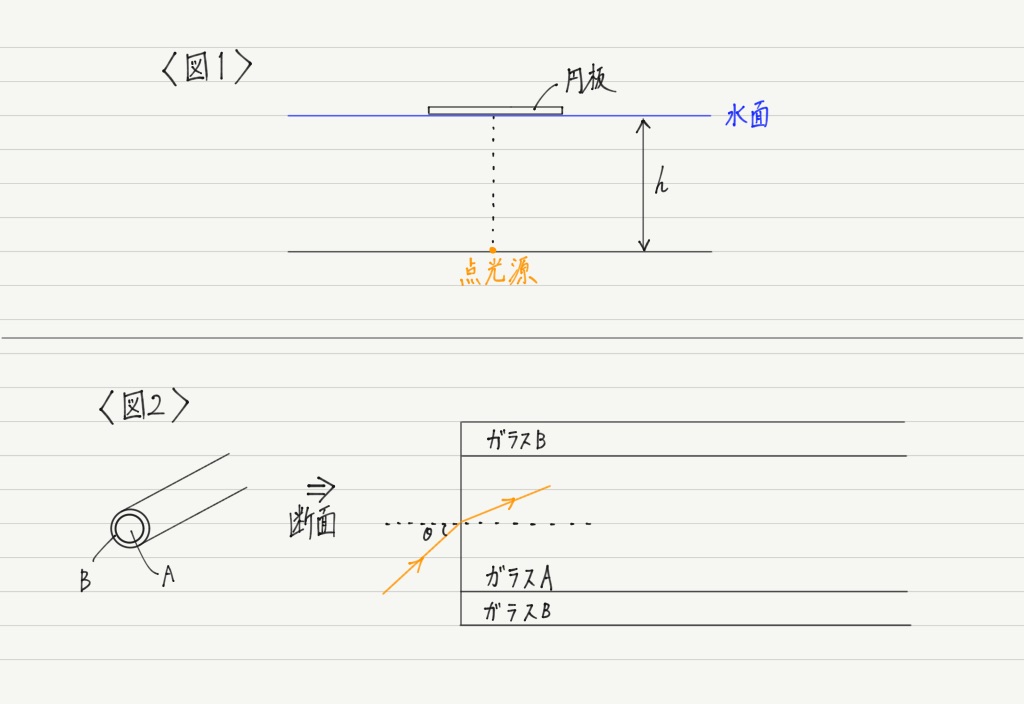
図1のように，水面からの深さhの地点に点光源を置く。 水面に円板を置くことで，点光源が外部のどの位置からも見えないようにしたい。 このために必要な円板の最小半径を求めよ。 ただし空気の屈折率を1，水の屈折率をnとする。
[Level.3]
屈折率nAのガラスAの外周を，屈折率nBの別のガラスBで覆った円柱状の物体があり，図2はその断面図を表している。 円柱の中心軸に入射角θで入射した光が，ガラスA中を進み続けるためには，sinθはいくらより小さくなければいけないか。 ただし，nA＞nBであり，物体は空気中（屈折率1）に置かれているものとする。
この下に答えを載せていますが，まずは自力で考えてみましょう。
答え
[Level.1]
30°
[Level.2]
\(\frac{h}{\sqrt{n^{2}-1}}\)
[Level.3]
\(\sqrt{{n_{A}}^{2}-{n_{B}}^{2}}\)
Sponsored Link
