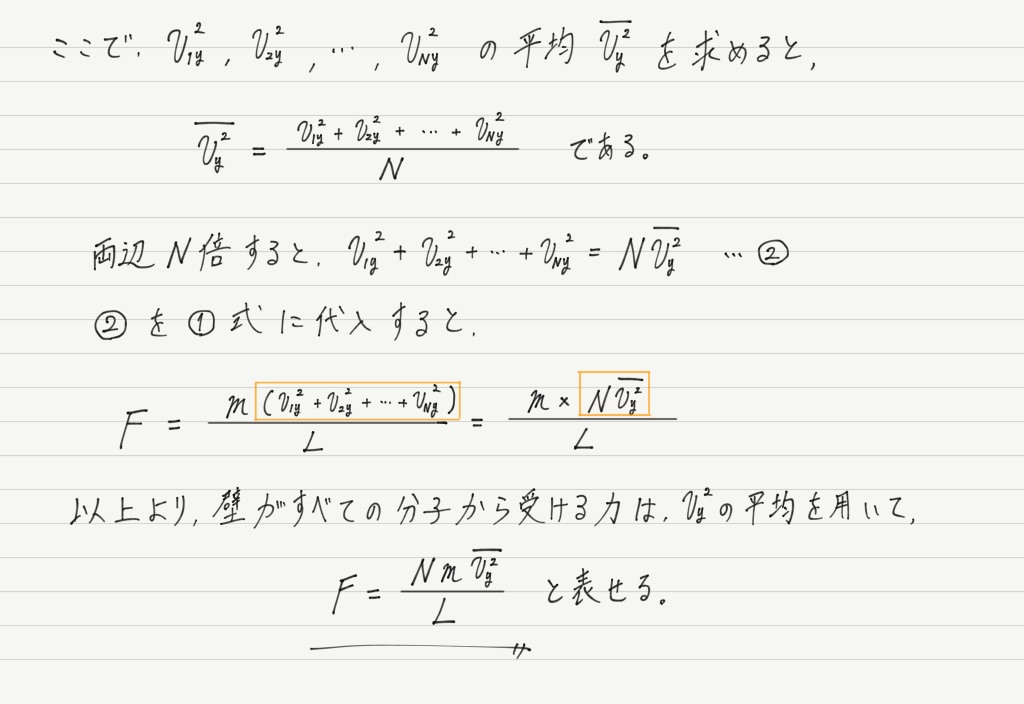前回の記事の続きです。 未読の方はまずは①に目を通してください。
前回得られた計算結果を使って，さらに話を進めていきましょう！
目次
手順５：すべての気体分子が壁に与える力を求める
手順4で，1個の気体分子が壁に与える力を求めましたが，容器には全部でN個の分子が入っているので，
ここでは壁が受ける力の合計を求めましょう。
平均を用いるのがポイントです。
ただし，「vの平均の2乗」ではなく，「vの2乗の平均」であることに注意してください。
足して2で割る平均（相加平均）ではなく，かけてルートをとるタイプの平均（相乗平均）はあまり見慣れないかもしれませんが，2乗平均速度は分子の速さを表す目安として熱の分野ではよく用いられます。
手順６：壁が受ける圧力を求める
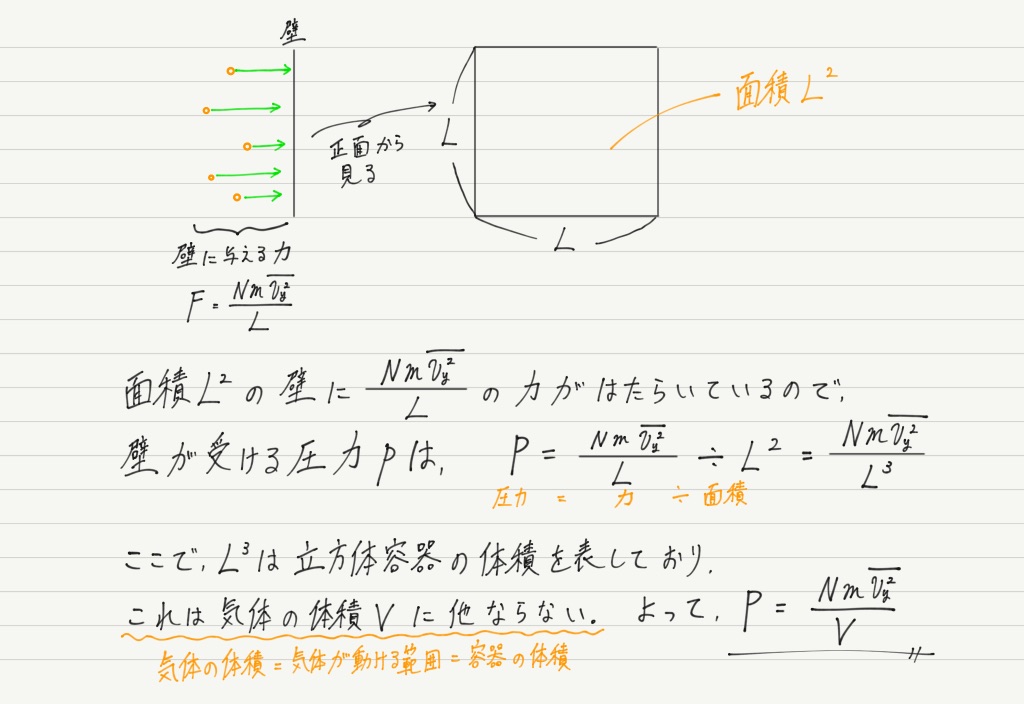
長い道のりでしたが，これで壁が受ける力が分かりました。
壁は1辺の長さがLの正方形なので，壁が受ける圧力は簡単に計算することができます。
これで気体の圧力が分子の運動から計算できました！ 感動で涙が止まらない。
それどころか，しれっと気体の体積まで登場してきました！ 涙で明日が見えない。
手順７：vのy成分ではなく，vそのものを用いて圧力を表す
手順6まで，y方向に注目して計算してきましたが，x方向やz方向に注目しても同じ計算が成り立ちます。
圧力が速度の成分で表されるのはちょっと微妙なので，速度そのものを用いて表すことにしましょう！
お，うまくいきましたね！
これは重要な結果なのでまとめておきましょう。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
圧力の式が求められて，ようやく気体の話っぽくなってきました。
次回はこの式を式変形して遊んでみましょう！
