自然現象を数理モデル化し，それを調べるのが物理という学問。
そのために様々な数学を駆使していくことになるわけですが，その中でも微分や積分は非常に強力な武器となります。
これまでに学んだいくつかの例を題材に，物理において微分積分がどのような役割を果たしているのかを見ていくことにしましょう。
諸注意
さて，今回のテーマは微分積分を用いた物理。
真面目に高校物理を勉強してきた人ほど，微分積分を用いた物理の説明を聞いて感動する傾向にあります。 私もかつて感動したし，皆さんにもぜひ感動してほしいと願っています。
でもだからこそ，微分積分を使わない物理をまずはマスターすべきです。
微分積分による公式の導出はいわば近道。 まずは普通の道順を知っていなければ，近道の存在を知っても感動することはできません！
それからもちろん，微分積分が苦手な人も感動できないでしょう。
よって，これより先は高等学校物理，および数学Ⅲを履修済みの方のみお進みください。 該当しない方，ごめんなさい。
条件を満たしている方は，微分積分の魔術をご堪能ください！
瞬間の速度・加速度と微分積分
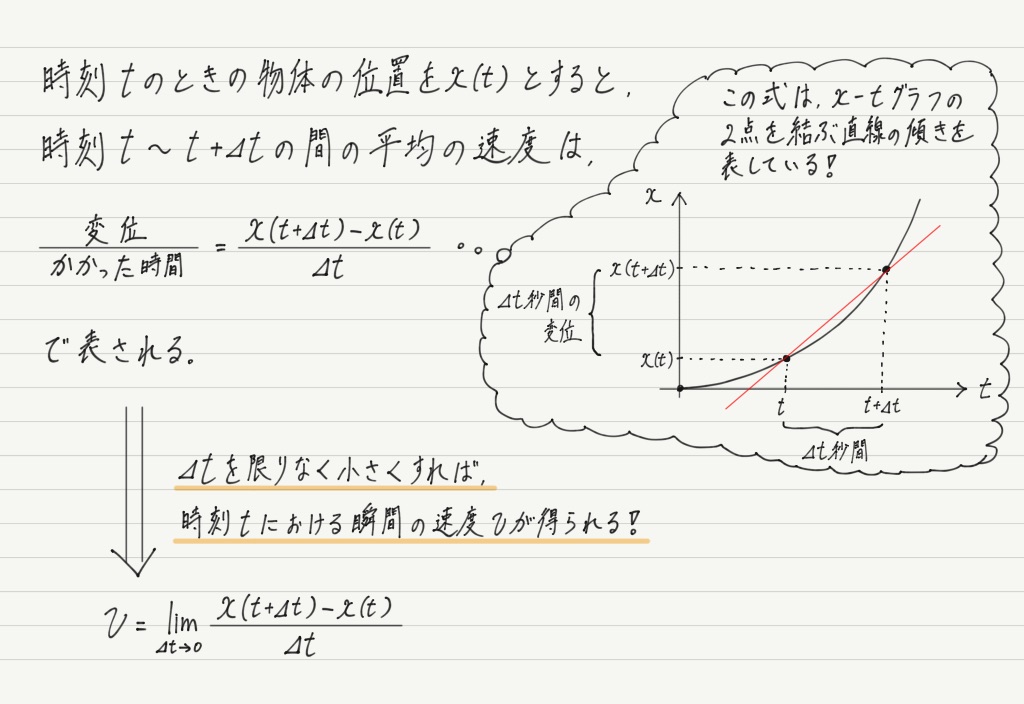
まずは力学の復習から。 運動している物体の⊿t秒間の平均の速度の，⊿tをきわめて小さくしたものが瞬間の速度でした！
あれっ？ この式どこかで見覚えが…
ピンときましたか？
そう，この式は導関数の定義そのものじゃないですか！！
微分は数学的にはグラフの接線の傾きを表すので，「ある時刻におけるx-tグラフの接線の傾き＝その時刻での瞬間の速度」というのも当たり前。
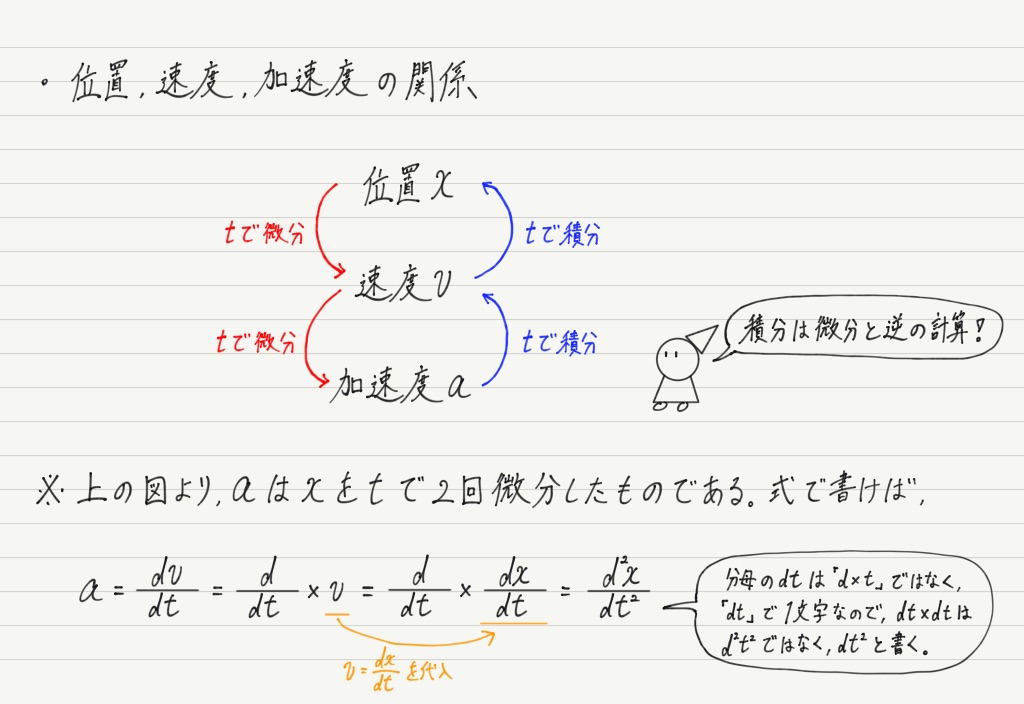
瞬間の加速度についても同様のことが成り立ちます。
まとめると，
せっかくなので実際に計算してみましょう！
導出が面倒な公式たちですが，微分や積分を使えばこの通り一発です。
運動方程式と運動量
力学における最重要法則，運動方程式の両辺を時間tで積分してみましょう。
ハイ，運動量と力積の関係が出てきましたよっと。
ん？ この積分といい，さっきのsinωtの微分といい，微分の記号を約分して大丈夫なのかって？
確かに数学の先生は「これは分数みたいに書いてあるけど，分数じゃないからな」って注意するので，その抗議はもっともです。
でもよく考えてみてください。 分数じゃないものをなんでわざわざ分数に似せて書いているのかを。
これはズバリ，「分数じゃないけど，分数みたいに約分してもいいよ」という意味合いなのです。 本当は証明すべき事柄ですが，便利なのでガンガン使わせてもらいましょう！
位置エネルギーと積分
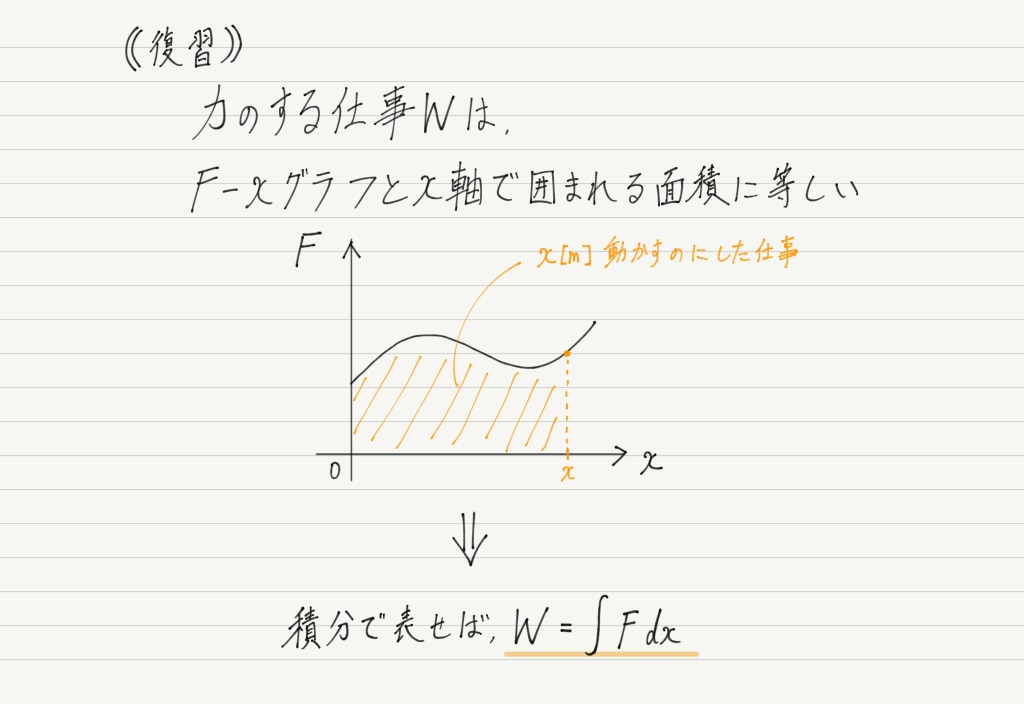
次は仕事について。 仕事＝F-xグラフで囲まれた面積なので，これは積分と関連づけられます！
力Fとして保存力を考えると，積分を利用して位置エネルギーを求めることができます！
（例1，2，3は，軸と力の向きを考慮してマイナスをつけているが，例4の異符号の場合はq×Q＜0であるから，マイナスをつける必要はない。）
保存力ってなんだっけ？という人は積分してる場合じゃないので，ただちに復習してください！
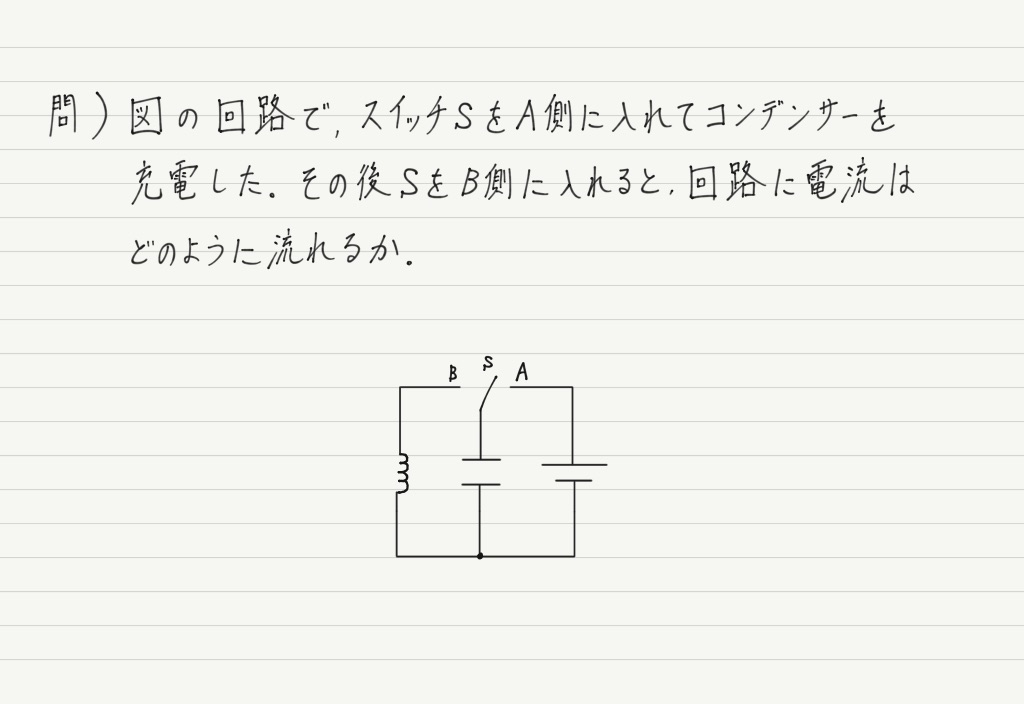
交流回路と微分
微分積分の活躍の場はなにも力学だけではありません。 電磁気，特に交流分野では大活躍です。
微分積分なしでは暗記するしかなかったコイルやコンデンサーのリアクタンスや位相のずれを計算で求めてみましょう！
この導出方法を理解しておけば，テスト中に「あれ？位相は進むんだっけ？遅れるんだっけ？」というパニックに陥っても大丈夫！
単振動と微分方程式
単振動を題材に，最後にもう一度運動方程式を扱っておきましょう。
力学の単振動の回では，「運動方程式がma＝−Kxの形をしていたら必ず単振動」と学習しましたが，一旦そのことは忘れて，純粋に数学的な観点から見直してみましょう。 加速度aを位置xの2階微分で置き換えると，運動方程式は微分を含む方程式（微分方程式という）となります。
（関数がsinかcosかは物体の初期位置で決まるが，どっちにしても振動することには変わりないので，今は気にしなくてよい。）
なんと，物理的な議論を一切せずに「この方程式の解は振動する」ということが導けてしまいました…！ 恐るべし数学の力…！
他にこんな例も挙げておきます。
さて，式を使って計算してみましょう。
おや？ この式って…
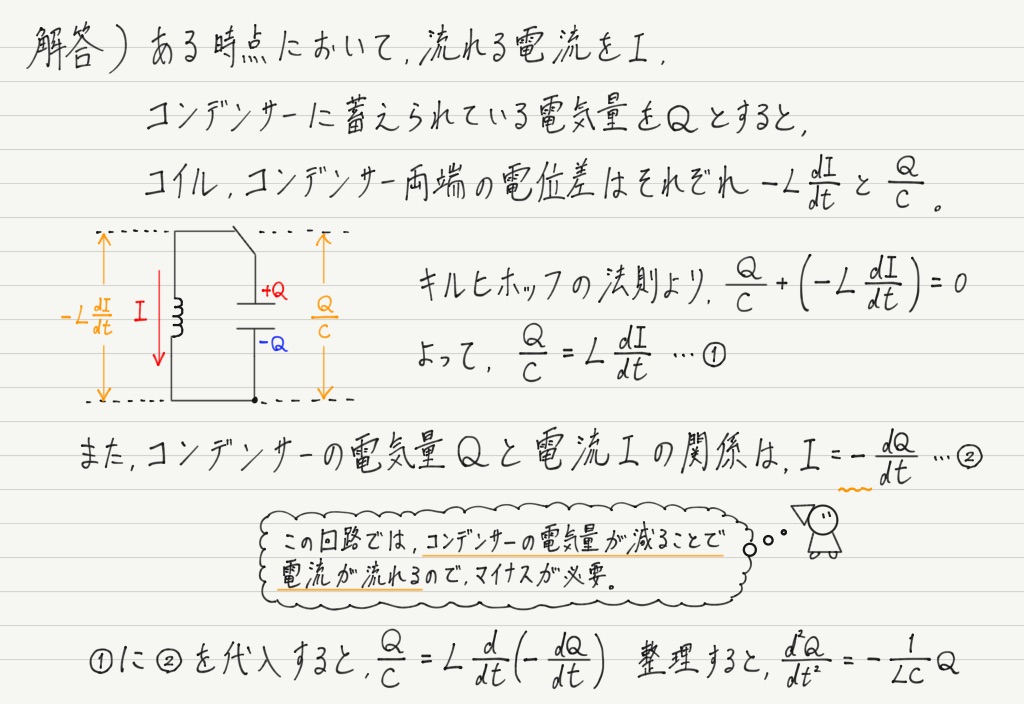
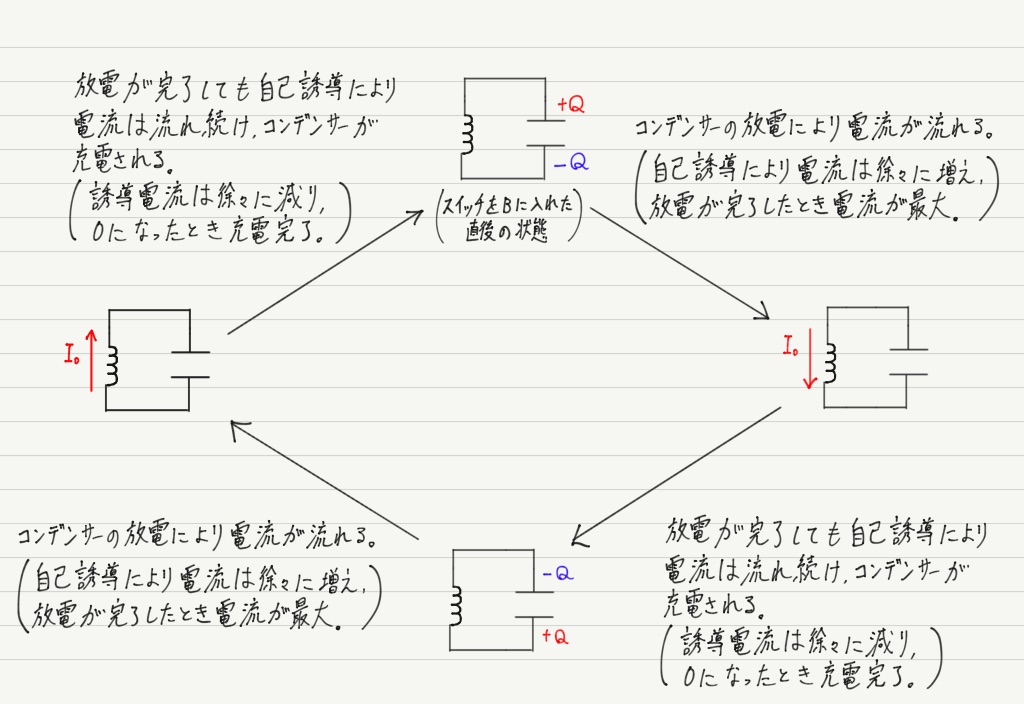
これまたビックリ！ 計算だけでLC並列部が振動（電気振動）することが示せました！
ちなみに計算を使わずに説明しようとすると，
うーん，計算だとほんの数行なのに，言葉で表すとこんなに長い…
やっぱり式で表すってすごいですね(^_^;)
（でも，高校物理としては現象をイメージするほうが大事！）
まとめ
高校物理で微分積分を用いて説明するのには基本的に反対だけど，「高校を卒業する段階で，物理と微分積分の関係を全く知らないというのも，それはそれで困る」という本音もあって（笑），この記事を書きました。
ここまで読んで，「微積すげー」と感動した人もいるかと思います。 ただし，感動の勢いあまって「物理の本質は微積分！」などと言い出さないようにしてください笑
物理の本質はどこまで行っても現象の理解。
「微分・積分の計算ができること」と「物理を理解していること」は完全に別物です。
そもそも理系なんだったら微分や積分なんてできて当然。 「ちゃんと現象を理解できているか？」という自問を忘れてはいけません。
大学の物理ではそれこそ微分方程式が山のように出てきますが，計算に翻弄されて物理を見失わないように心がけましょう！
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！
