物理のヒント『物理と微分積分』の講義内容に関連する演習問題です。
講義編を未読の方は問題を解く前にご一読ください。
問題
[Level.1]
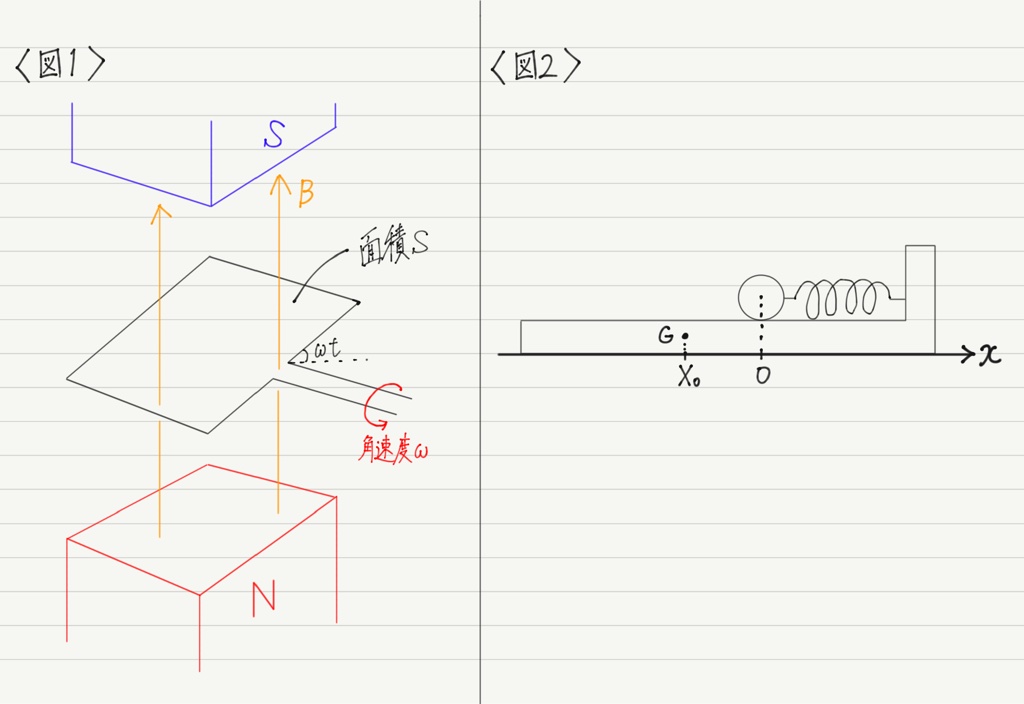
図1に示すように,鉛直上向きの一様な磁束密度Bの磁場中で面積Sの1回巻きコイルが一定の角速度ωで回転しており,時刻tにおいて水平面とコイルの面のなす角がωtであるとする。
このコイルに生じる誘導起電力Vを求めよ。
[Level.2]
x-y平面上の原点を中心として,半径r,角速度ωで等速円運動をする物体の位置が時刻tの関数として(rcosωt,rsinωt)で与えられているとする。
どの時刻においても物体の加速度が円運動の中心を向いていることを示せ。
また,加速度の大きさがrω2であることを示せ。
[Level.3]
水平でなめらかな床の上に質量Mの台が置かれている。
この台の右端と質量mの小球をばね定数kのばねでつなぎ,ばねが自然長となるように小球をなめらかな台上に静かに置いた(図2参照)。
このときの台の重心Gの位置を小球の位置を原点とする床に固定されたx座標で表すと,x=X0であった。
時刻t=0において小球のみに初速度v0を与えたところ,小球は台に対して振幅d,角振動数ωの単振動をはじめた。
時刻tにおけるGの位置を求めよ。
この下に答えを載せていますが,まずは自力で考えてみましょう。
答え
[Level.1]
V=BSωsinωt
[Level.2]
時刻tでの加速度は(-rω2cosωt,-rω2sinωt)と求められる。
これは位置ベクトルの向きと逆向きなので,原点に向かっていることがわかる。
加速度の大きさは三平方の定理を用いればよい。
[Level.3]
\(\frac{m}{M+m}(v_{0}t-d\sin \omega t)+X_0\)