本格的にエネルギーの話に入る前にいったん寄り道。 仕事について学んだところで,力の話に戻ります。
とは言ってもここで新しい力が登場するわけではなく,これまでに学んだ力を「ある性質」に注目してグループ分けしてみましょう,というお話です。
物体を運んでみよう その1
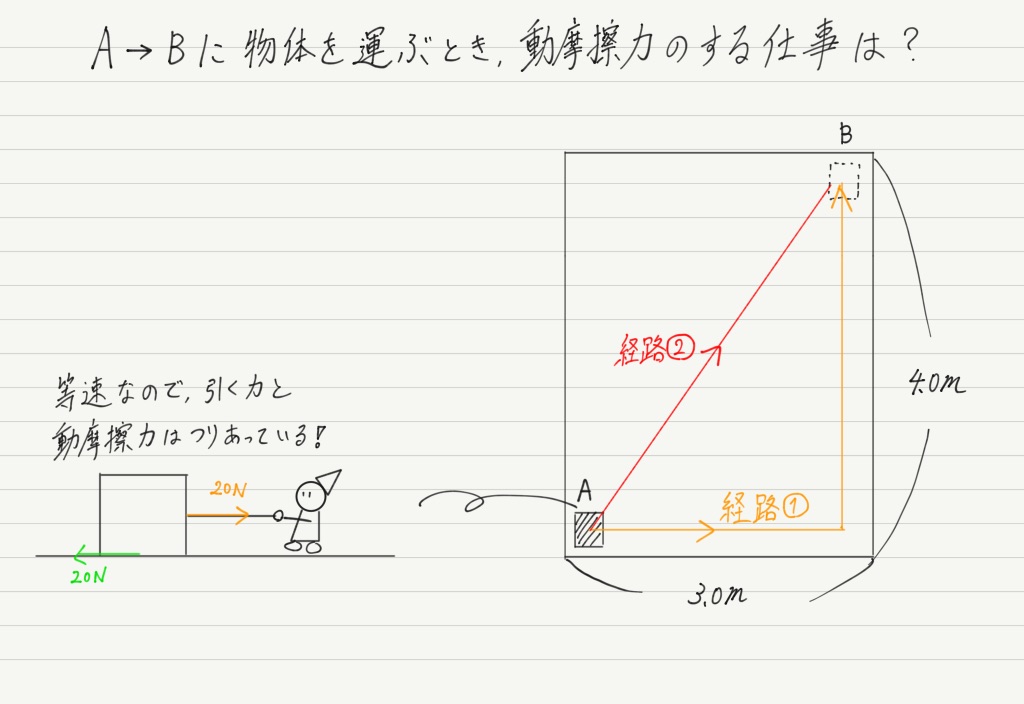
下の図は,ある部屋を真上から見たものです。
図のA地点にある物体を,20Nの一定の力で引っ張り,B地点まで等速で移動させます。
今回考えたいのは,AからBへ運ぶとき,運ぶ経路によって動摩擦力がする仕事の量が変わるか,ということです。
では実際に求めてみましょう。
まず,①の経路では物体を壁沿いに運んでいるので,AからBまでの総移動距離は3.0m+4.0m=7.0m。 よって動摩擦力のする仕事は,20N × 7.0m ×(ー1)= ー140Jです。
なぜマイナスが付くんだっけ?と思った人は要復習 ↓
一方,②の経路は対角線上を運ぶので,移動距離は5.0m(対角線の長さは三平方の定理で求められますね!)。 よって動摩擦力のする仕事は,20N × 5.0m ×(ー1)= ー100Jです。
上の計算結果を見比べると,どの経路を通るかによって,動摩擦力のする仕事は変わるということが分かります。 この場合の動摩擦力は邪魔をする力なので,距離は短いほうが邪魔されずに済む,というのは当たり前ですが (^_^;)
物体を運んでみよう その2
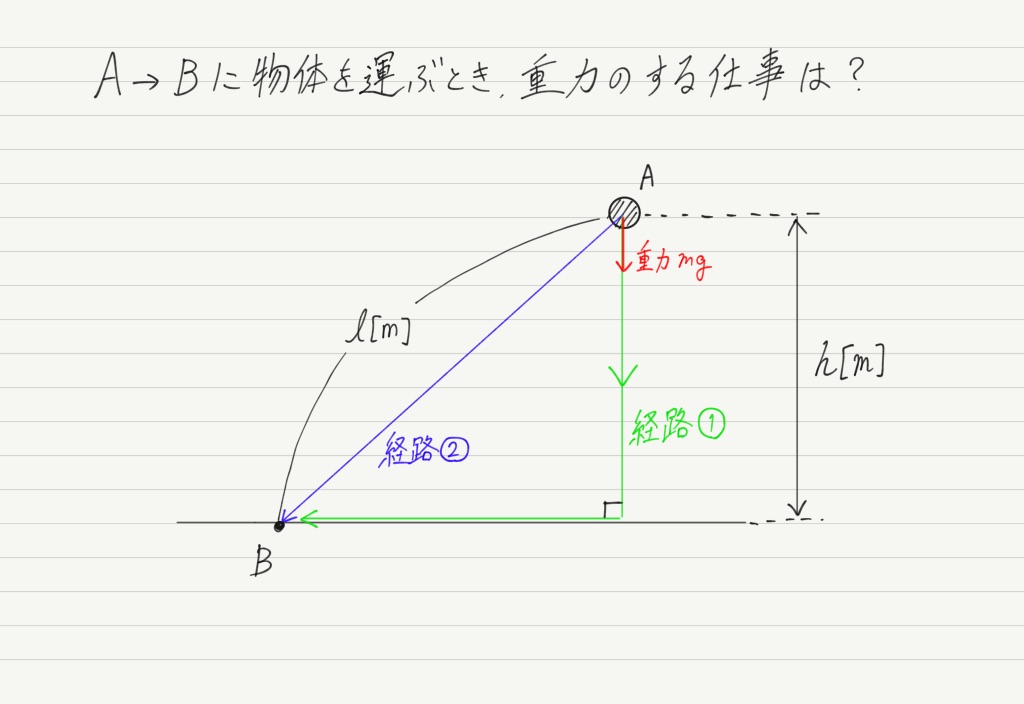
次は,物体を高いところから低いところへ持っていくとき,重力がする仕事について考えます。
①の経路は,まず真下,次に真横に移動させています。
真下に下ろすとき,重力の大きさはmg ,距離はhなので,重力のする仕事は,力 × 距離でmghです。
真横に動かすとき,重力の向きと移動方向は垂直なので,重力のする仕事は0です。
よって,①の経路の全体の仕事は,mgh + 0=mghとなります。
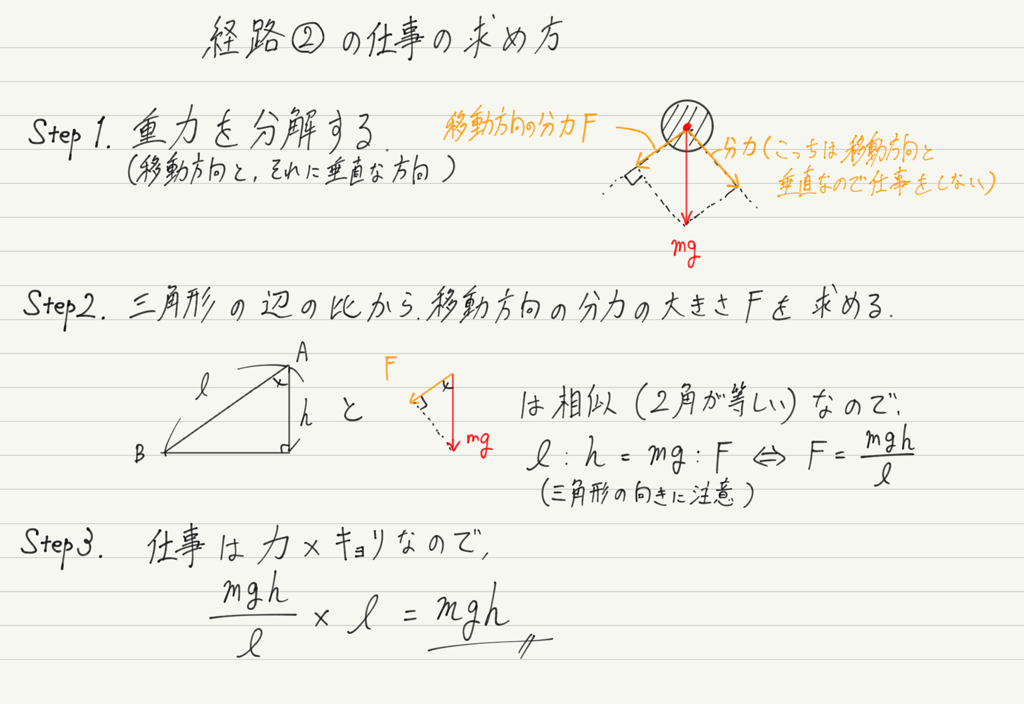
次に②の経路ですが,重力の向きと移動方向が同じ向きでも,逆向きでも,垂直でもないことに気をつけてください。
移動方向に対して力が斜めを向いている場合は力を分解して移動方向の成分を求め,その成分と移動距離をかけ算して仕事を求めます。
もし力の分解のやり方を忘れていたらコチラの記事をどうぞ↓
さて,上の計算の結果を見てみると,なんと②の経路でも重力のする仕事はmghとなっています!
あれ? どちらの経路で運んでも同じ仕事?
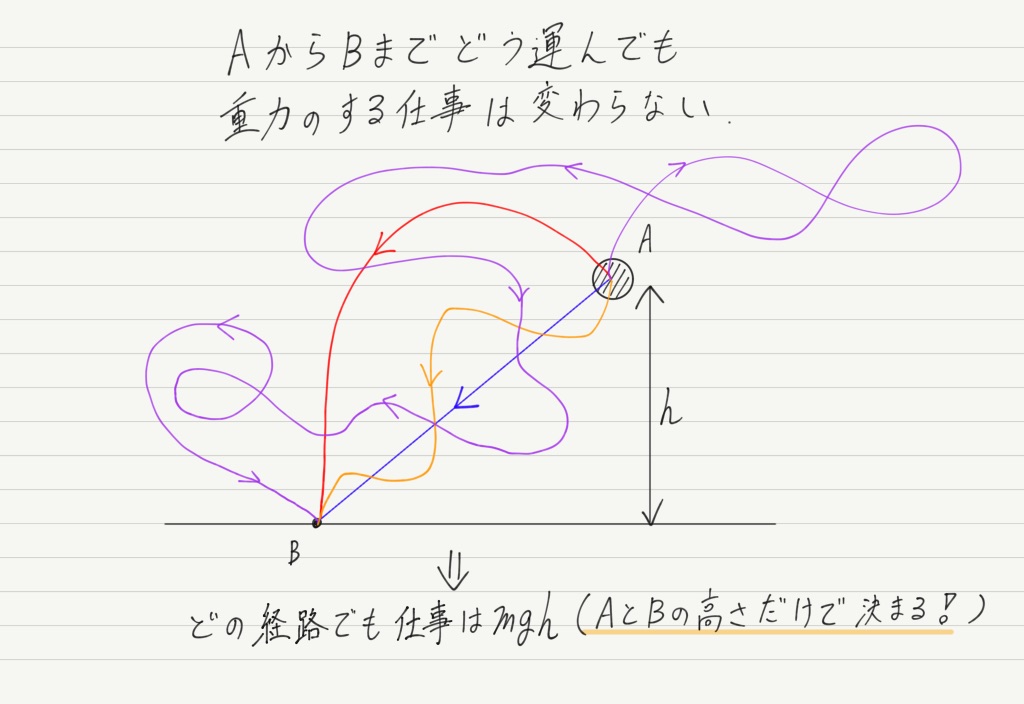
実は重力がする仕事というのは,物体をどの経路で運んでも常に一定であることが知られています。
上の例では2通りしか計算しませんでしたが,AからBまで,どんなに複雑な経路で運んだとしても,重力のする仕事は常にmghです!!
保存力とはなにか
以上の計算で何が分かったかというと,力には,「通る経路によって仕事の値が変わる力」と,「どの経路でも仕事の値が変わらない力」の2種類が存在するということ。
重力のように,どの経路を通っても仕事が変わらない力のことを「保存力」と呼びます。
「どの経路でも仕事が変わらない」というのは,言い換えると「出発点と到着点さえ分かれば,それだけで仕事が計算できる」ということです!! これは便利!
(たとえば,重力のする仕事は2点間の高さの差hが分かれば計算できる。)
一方,動摩擦力のように,経路によって仕事が変わってしまう力は「非保存力」と呼ばれます。
保存力の性質は仕事を計算するにあたって非常に強力なので,どの力が保存力なのかは絶対に覚えておきましょう!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は運動エネルギーのお話です!