前回までで,力学に登場する主な力の紹介が終わりました!(長かった!笑)
これ以降は物体の運動と力の関係を調べることがメインテーマになります。 今回はそれに向けて,力の取り扱い方を勉強しましょう。
① 力の合成
現実において,物体にはたらく力がひとつとは限りません。 むしろ複数の力がはたらいていることのほうが普通です。
物体に複数の力がはたらくとき,それらをバラバラに考えるのではなく,まとめて1つの力にしてしまった方が取り扱いが簡単です。
複数の力を合わせて1つの力とみなすことを力の合成といいます(合成してできた力を合力という)。
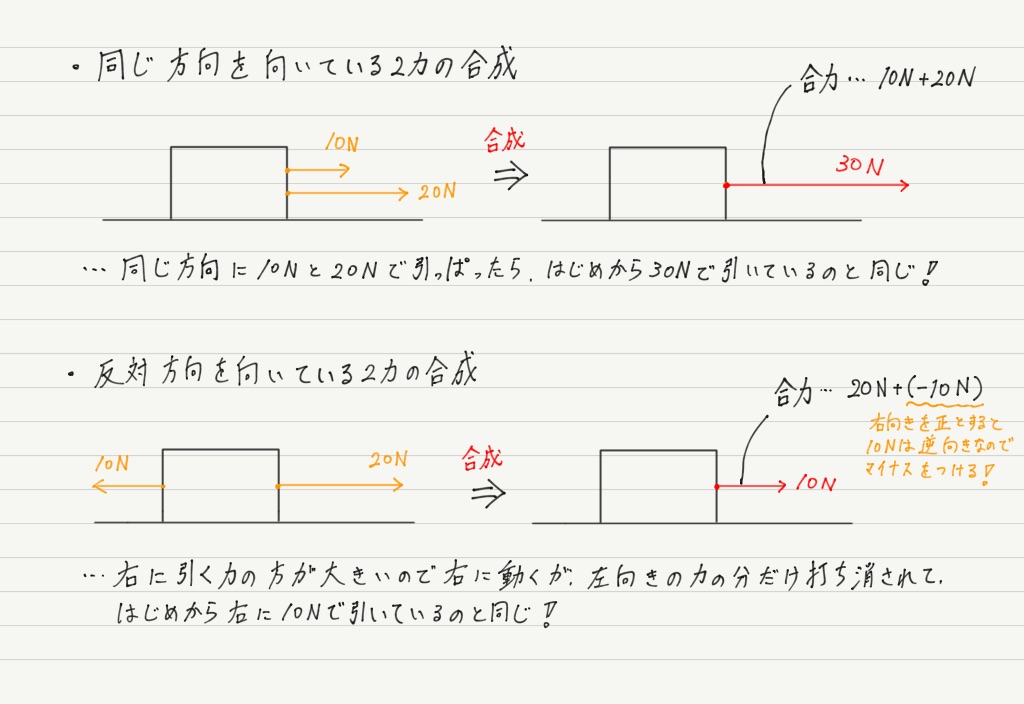
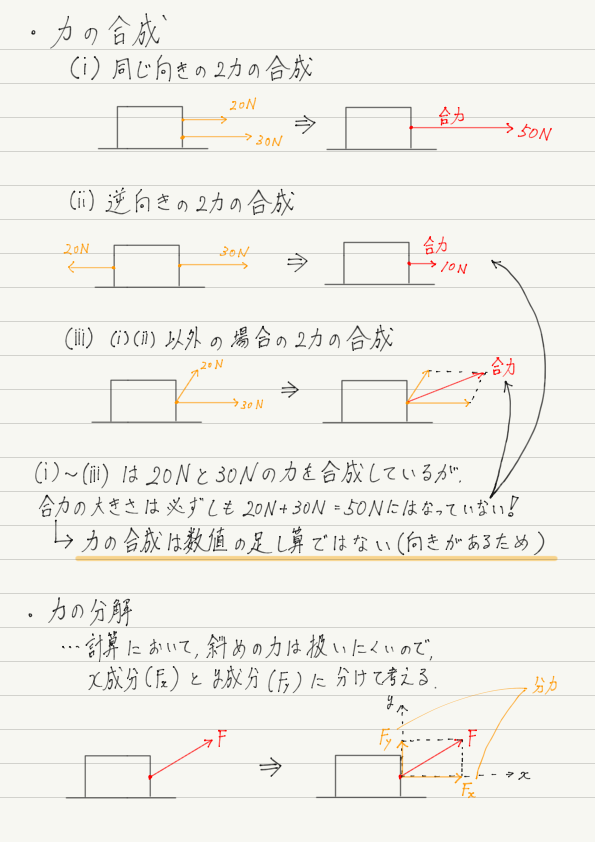
では,具体的に見ていきましょう! まずは2つの力が同じ方向 or 真逆を向いている場合です。
力の大きさを足したり引いたりするだけです。 これは簡単。
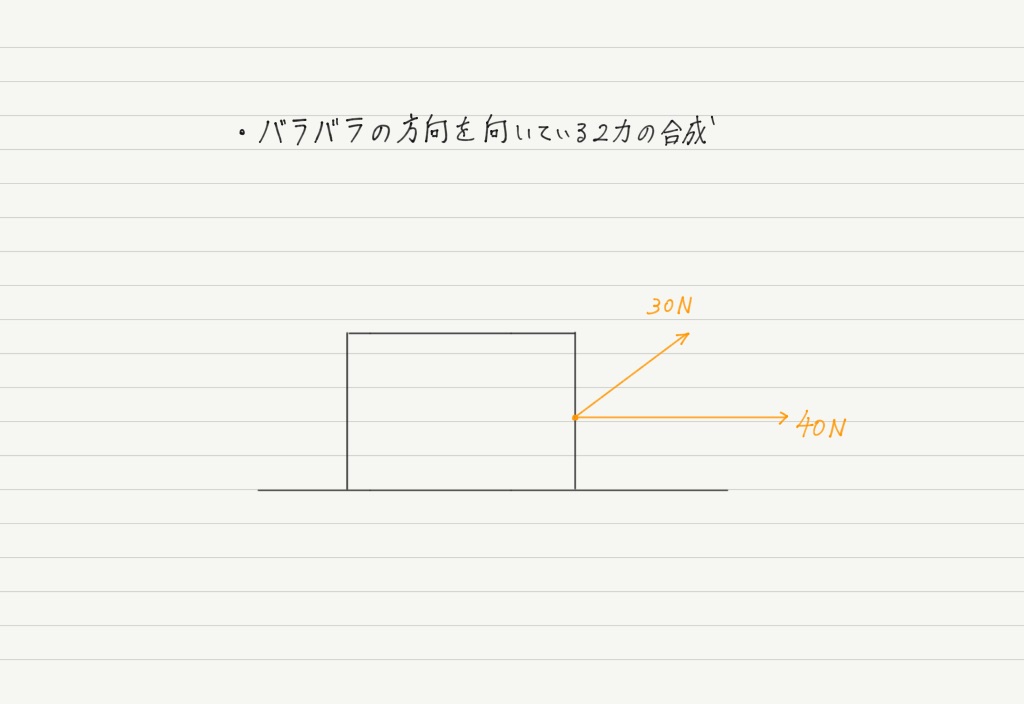
では,次の場合はどうでしょう?
30Nの力と40Nの力を合わせたから70N?
いいえ,ちがいます。
普通の足し算なら1+1=2 ですが,力の合成の場合,1Nの力と1Nの力を合成しても,2Nになるとは限りません!!
さっきの一直線上の場合を思い出してください。 同じ方向に1Nの力が2つはたらいていれば,合わせて2Nですが,逆向きなら,打ち消し合って0になってしまいます!
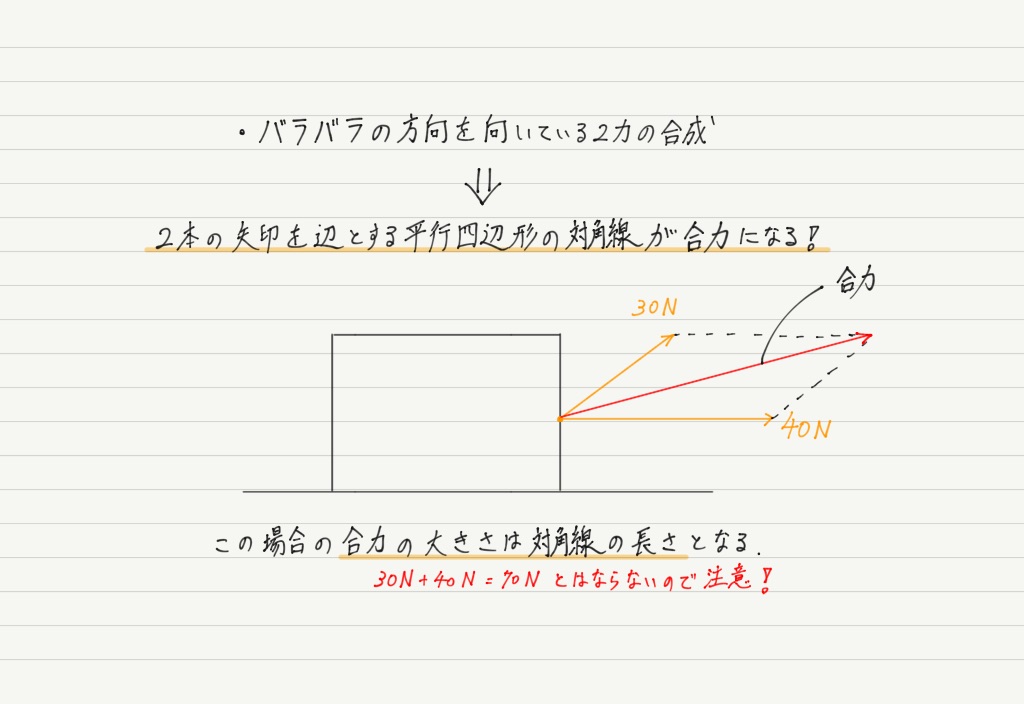
このように,力を合成するときは,“力の向き”が重要であることがわかります。 今回の場合も,2本の力の向きがそろっていないので,そのまま大きさどうしを足すのは間違い!!
向きの異なる力を合成する時は,平行四辺形を用います。
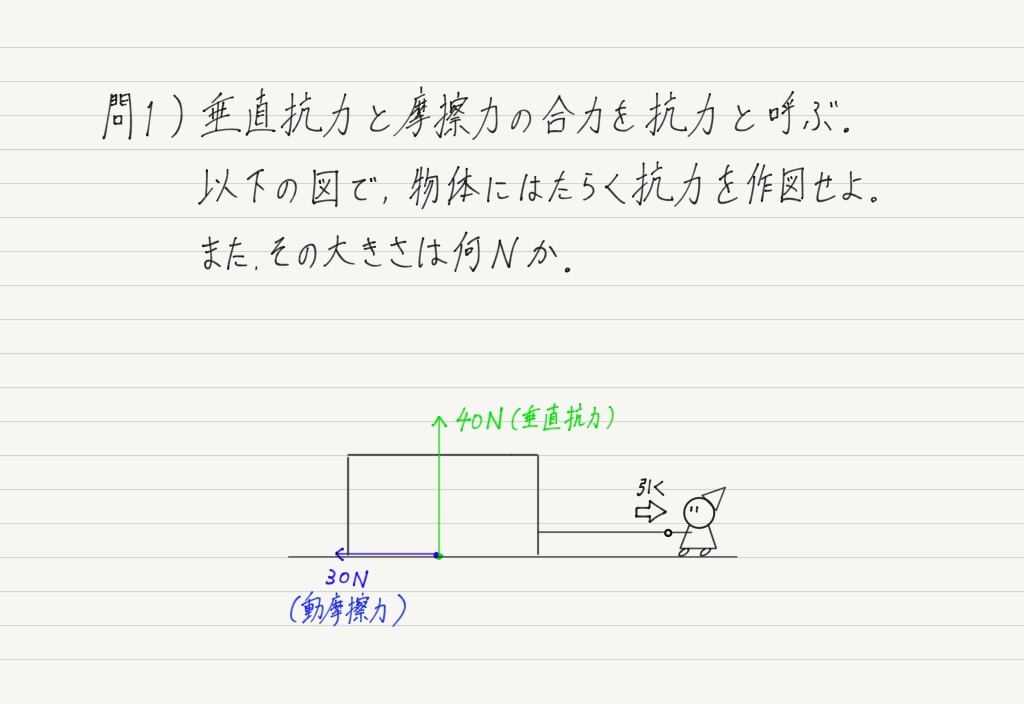
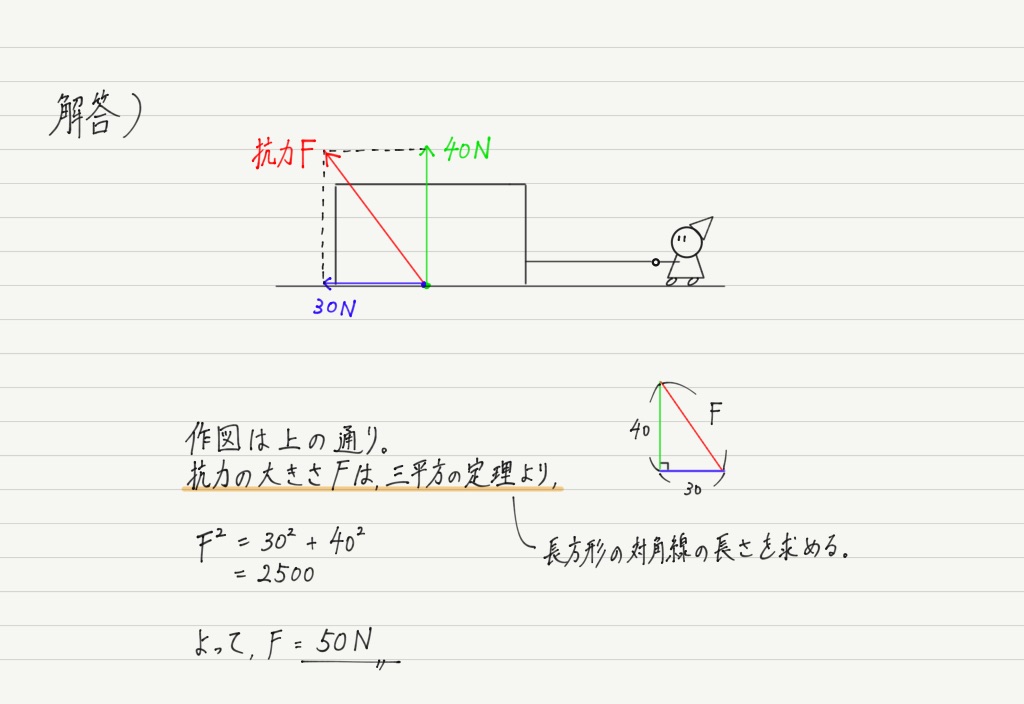
まとめとして,ひとつ問題をやってみましょう!
解答はこの下にありますが,まずは自分で解いてみてください。
では,解答です。
力が3つ以上あるような場合でも力の合成は可能です。 まずAとBを合成して,次にその合力とCを合成して…というように,ひとつひとつ合成していけばOK。
② 力の分解
2つの力を1つにするのが力の合成なら,1つの力を2つにするのが力の分解です。
「なぜわざわざ分けるんだ! 数が増えて面倒じゃないか!」という声が聞こえてきそうですね(笑)
もちろん,なんでもかんでも分解するわけではありません。
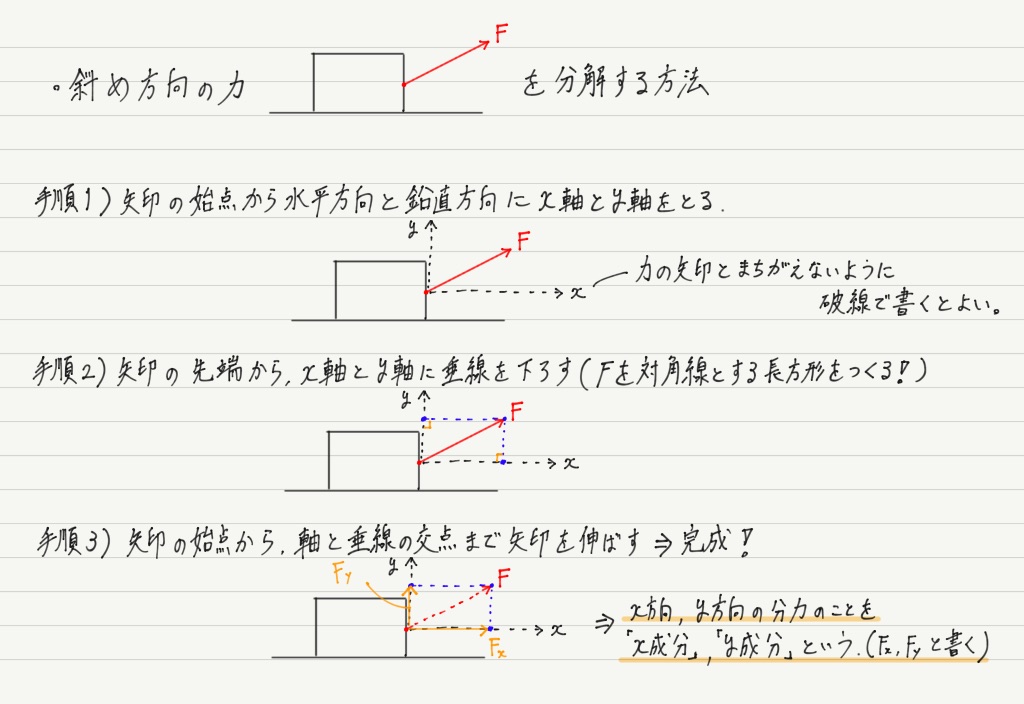
力の分解をしなければいけない場面はただひとつ。 「斜め方向の力」がはたらく場合です。
少し先のお話になりますが,物体の運動を調べる時は,「タテ(鉛直方向)とヨコ(水平方向)に分けて考える」ことが鉄則。 そのときに斜め方向の力があるとうまくいかないので,力を分解することになります。
右上を向いた力なら右方向と上方向に,右下を向いた力なら,右方向と下方向に分ける,という感じです。 具体的なやり方は下図を見てください。
これを見ると,力の分解とは力の合成の逆,ということが分かると思います。 こちらも問題をやってみましょう!
それでは解答を確認。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回も引き続き,力の計算をします!