物理の問題を解いているとたまに遭遇する近似計算。
近似方法は問題文に書かれていることがほとんどなので,「どうしてその近似が成り立つかわからないけど,とりあえず指示に従って計算しとくか」という人も多いのではないでしょうか?
今回は「なぜそういう近似になるのか」に焦点を当てて解説したいと思います!
① 微小量の累乗に関する近似
いくつかある近似計算の中でも一番オーソドックスなのはコレ↓
0.0000000001は小さすぎてさすがに無視しちゃってもよさそうだよね,ってことで0に近似しちゃってます(「≒」は「ほとんど同じ」という意味を表す記号)。
「ん? x自体がめちゃくちゃ小さいんだったら,いっそ x ≒ 0にしてしまえばよくない?」…と考える人がいますが,さすがにそれは雑すぎてアウト。
え? 納得できない?
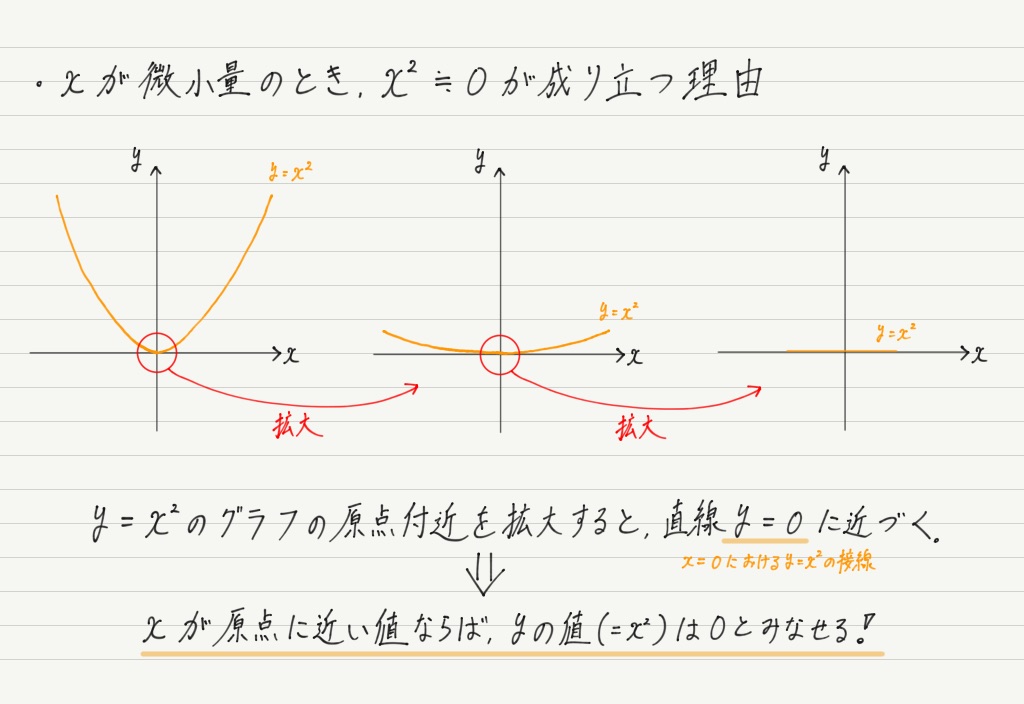
ではグラフを使って説明しましょう!
キリがないので書きませんが,xの3乗,4乗,…のグラフも同様に,原点付近を拡大するとx軸上の直線になるため,微小量のn乗(n≧2)はすべて0に近似できます。
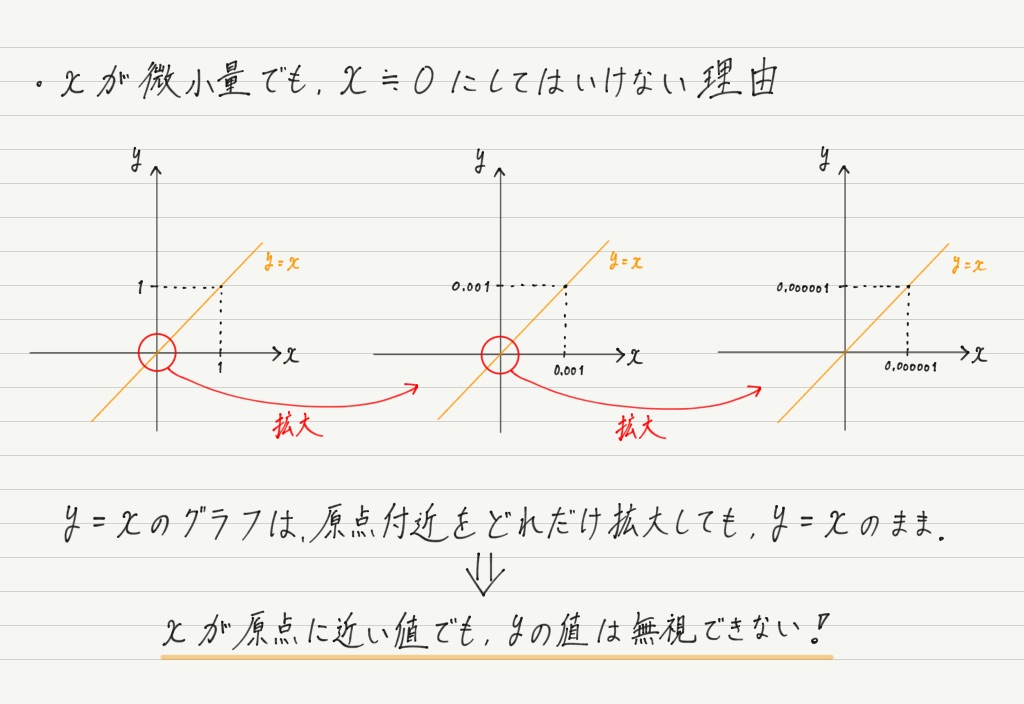
一方,n=1の場合はというと…
言葉だけで説明するのには限度がありますが,グラフを使えばこの通り。
近似の真髄はグラフにあり!?
② (1+微小量)の累乗に関する近似
以下の近似は物理ではド定番です。
この近似式を不思議がることはありません。
なぜならこれはさっきの「微小量のn乗 ≒ 0」の応用に過ぎないからです。
この近似式の有用な点は,nが整数でなくても成り立つこと(証明は高校範囲から外れるため省く)。
その場合の近似はヤングの実験の計算で使います。
③ 三角関数に関する近似
最後に三角関数の近似について解説します。
近似ということですが,三角比の話なのでとりあえず直角三角形を書いて考えてみましょう。
これでなんとなくこの近似の意味は理解できると思うのですが,次のような疑問をぶつけられることが多いです。
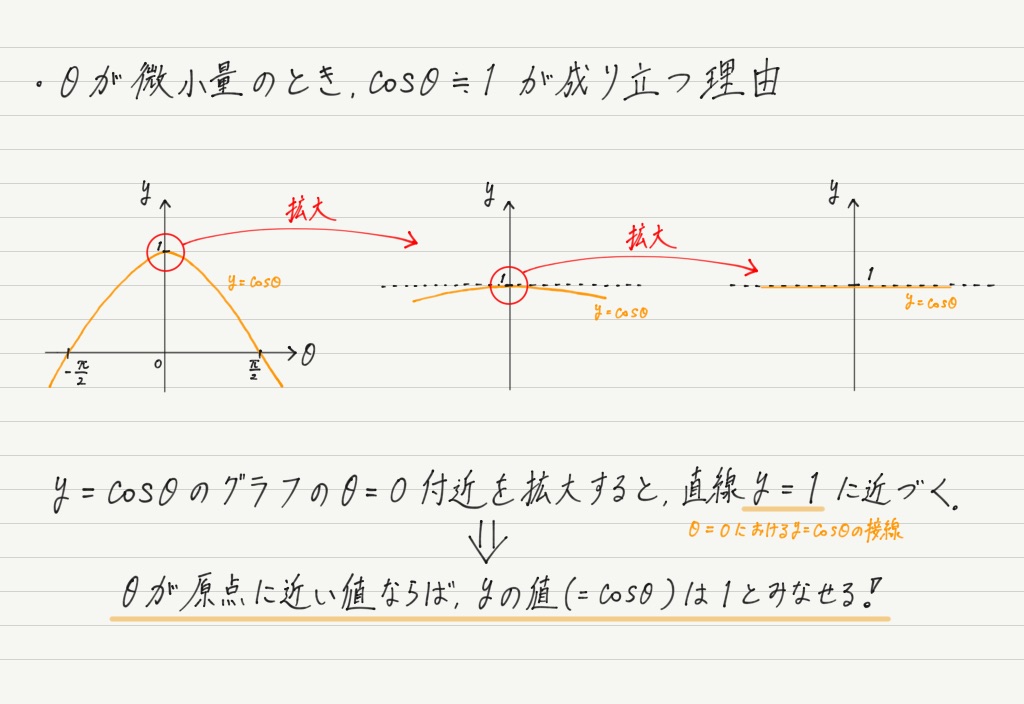
「cos0=1だから,θが小さいときcosθ ≒1はわかる。 だけど同じ要領で考えたらsin0=0,tan0=0なんだから,sinθ ≒ tanθ ≒ 0じゃないの? なんでsinθ ≒ tanθ ≒ θなの?」
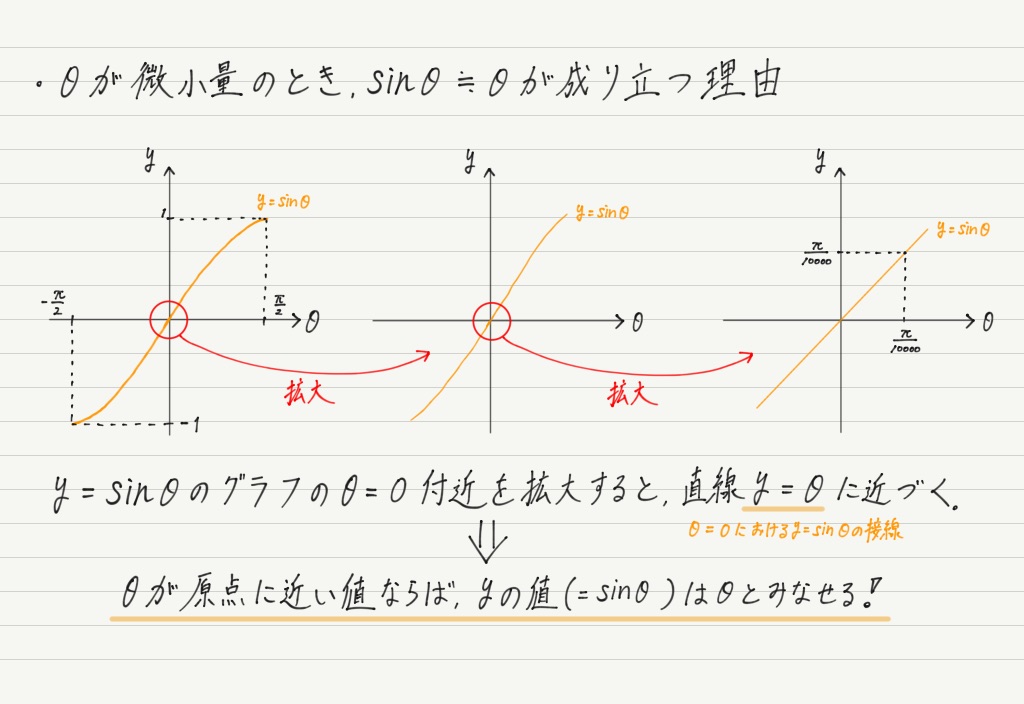
この疑問を解決するために,微小量のn乗と同様にグラフで考えましょう。
(※ 三角関数の接線の話が出てくるので,数学Ⅲで三角関数の微分を習っていることが望ましい。)
(y=tanθのグラフもy=sinθのグラフと同様,θ=0における接線はy=θになるので,θが原点に近い値ならばtanθ ≒ θが成り立つ。)
近似の疑問がまたまたグラフで解決しました。 いやぁ,グラフって偉大!
物理学と近似
今回は近似計算について解説をしましたが,「近似ってことは正確な値じゃないってことでしょ? それってなんだか気持ち悪いなぁ」と思う人もいるでしょう。
これだけは言わせてください。
物理ってそもそも近似の学問だから!
現実で起こるあらゆる現象を単純化(近似!)したモデルを扱うのが物理。
というか,うまく単純化できたものだけをすくい上げて,それを「物理」と呼んでいるだけなのかもしれません。
たしかに近似は正確ではないかもしれないけど,ガリレイが摩擦や空気抵抗を無視した思考実験によって慣性の法則を得たように,うまい近似はむしろ本質を見抜くことにつながります。
物理を学ぶ限り近似はいつまでもついてまわるので,うまく付き合っていきましょう!
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください!