円運動の問題を解くだけならここまでに学習した内容だけで十分なのですが,最後のトピックとして遠心力を学びましょう。
遠心力というのは物理を履修していない人でも知っている有名な力ですが,物理で取り扱う際には注意が必要な,ある意味 “特殊な” 力です。
通常の力と何がちがうのかをしっかり理解してください!
遠心力の向きと大きさ
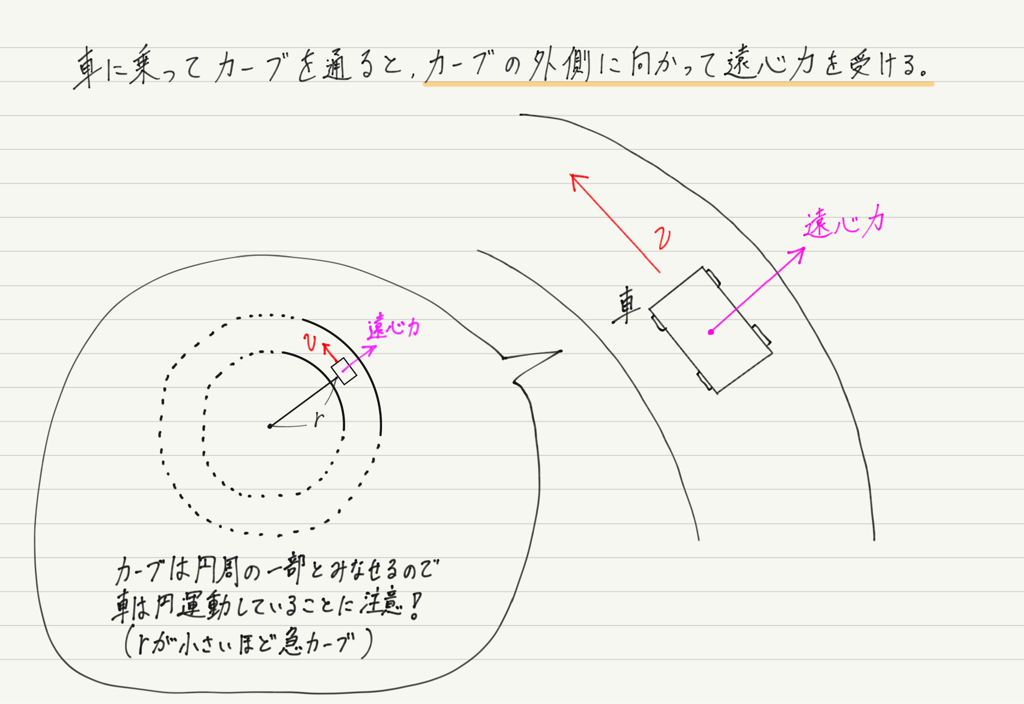
遠心力を感じるシチュエーションといえば,カーブを曲がる車の中!
カーブの外側に向かう方向に引っ張られる感覚があるはずです。
(カーブは円周の一部なので,カーブを曲がる車は部分的に円運動をしていることに注意!)
というわけで遠心力の方向は明らかですが,その大きさはどうなるでしょう?
遠心力を強く感じるときもあれば,ほとんど感じないときもあります。
これまたカーブを曲がっている車中を想像してください。
我々の経験から,遠心力の大きさは物体の速さとカーブの緩急(=円運動の半径の大小)に関係していると考えられます。
なぜなら,
・速いスピードでカーブを通過しようとするほど,車中の人が受ける遠心力は大きい
・同じスピードであっても,ゆるやかなカーブよりも急カーブを曲がっているときのほうが遠心力は大きい
からです。 経験あるよね?
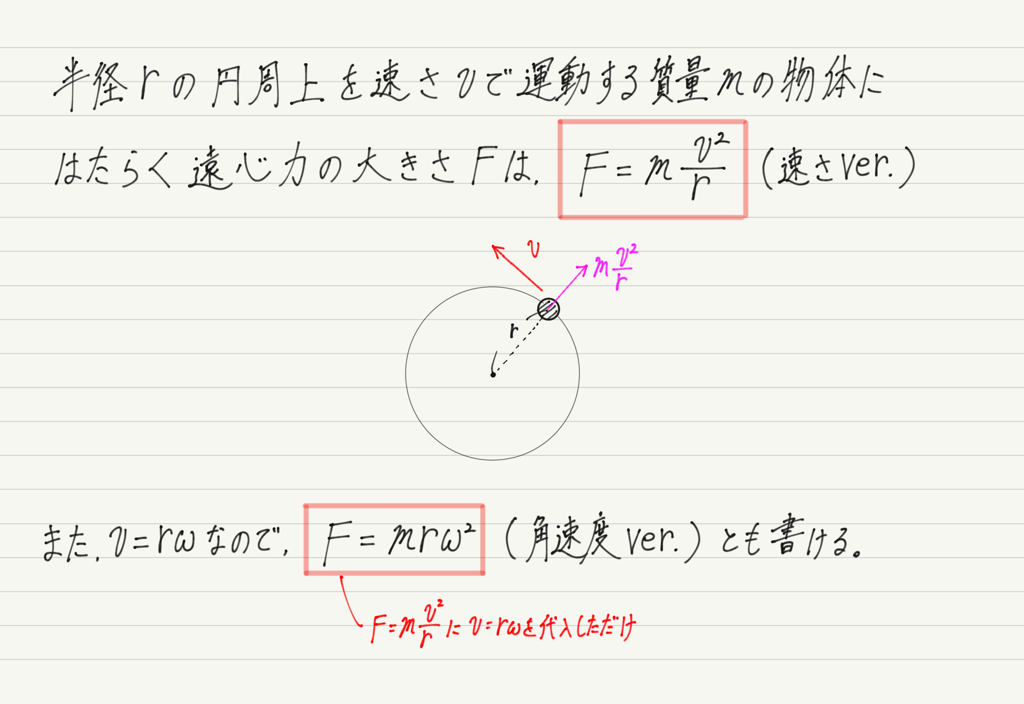
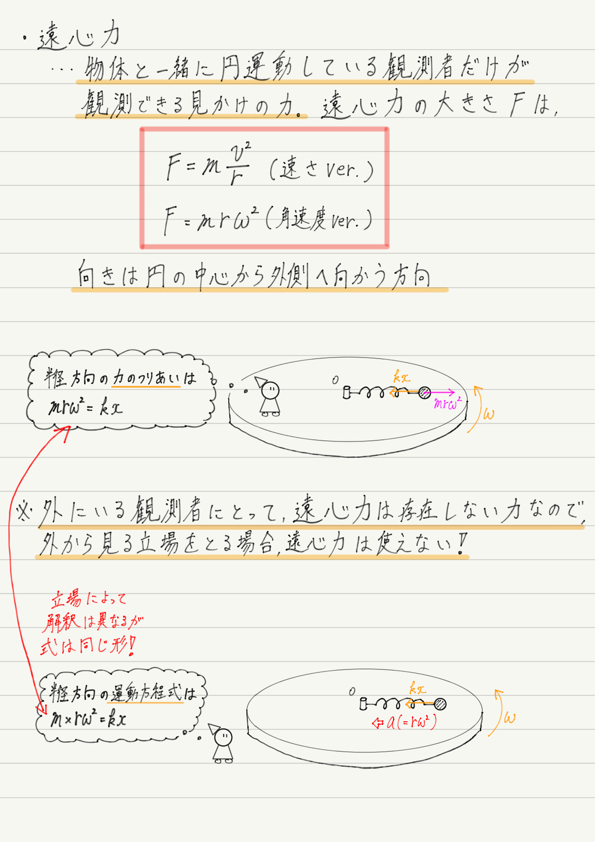
ということで結論ですが,遠心力の大きさは次の式で求めることができます!
式を見ての通り,実は遠心力の大きさは速さと半径だけでなく,質量にも比例します。
このことは自分が “回る立場” だと分かりにくいですが,自分が “回す立場” で考えると理解しやすいです。
たとえば,水を入れたバケツをぐるぐる回しても水が落ちてこないという有名なやつ。
実際にやってみるとバケツを回す腕に遠心力を感じますが,バケツに入れる水の量を増やすとより強く遠心力を感じます。
遠心力の変な(?)性質
冒頭で「遠心力は “特殊な” 力だ」と書きました。
これまでに習った重力や張力などの “普通の” 力と比べて,一体どこが特殊なのでしょうか?
先ほど同様,車に乗っているところをイメージしてください。
カーブに差し掛かって,あなたは遠心力を受けます…
…何かおかしな点に気づきませんか?
「自 分 は 何 か ら 遠 心 力 を 受 け た の か ?」と… … …
重力は地球が,弾性力は変形したばねが,垂直抗力は面が,というように,力は必ず「AがBに力を及ぼす」という因果関係があります。
しかし遠心力では,この文章のAに該当するものが不明です(遠心力を受けているとき,車体に押されたり引っ張られたりしているわけではないので,A=車,ではない)。
何から及ぼされているのかわからないのに,確かに感じることのできる力。
これが遠心力の特殊な点。
さて,遠心力が何から及ぼされているかがわからないことから,次のような結論が導かれます。
① 遠心力には反作用がない。
② 遠心力は円運動している本人にしか存在を感知できない。
まず①について。
「AがBに及ぼす力」の反作用は「BがAに及ぼす力」ですが,遠心力にはそもそもAが存在しないため,反作用という概念もありません。
続いて②。 これが実際に問題を解く上での最重要ポイント。
力学では物体にはたらく力を書くことが何より重要です。
床に接しているから垂直抗力を表す矢印を書いて,糸に引かれているから張力を表す矢印を書いて…
というように力の矢印を書いていきますが,これは垂直抗力や張力が何から及ぼされる力なのかをあらかじめわかっているからこそ書けるわけです!
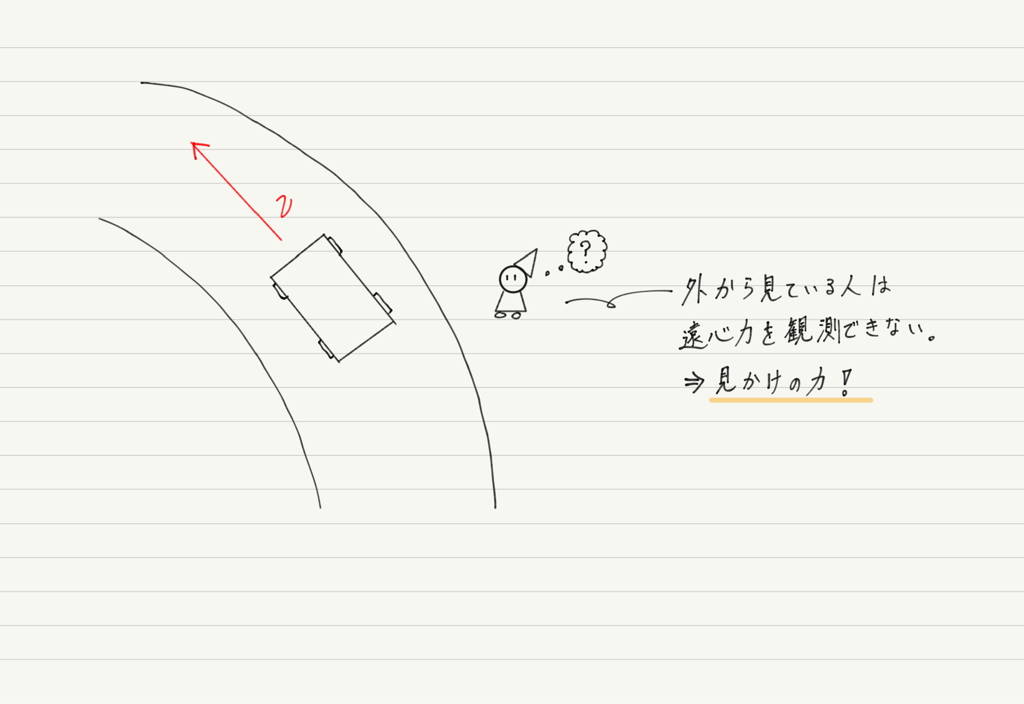
ところが遠心力は何から及ぼされる力なのか不明なので,実際に遠心力を受けている人以外はその存在を知る術はなく,遠心力の矢印を書くことはできません!
これはつまり,遠心力というのは実際に存在している力ではなく,円運動している人だけが感じる「見かけの力」だということ。
それでは,この「見かけの力」が円運動の問題を解く際にどう影響を及ぼすのかを見ていきましょう。
2つの異なる視点
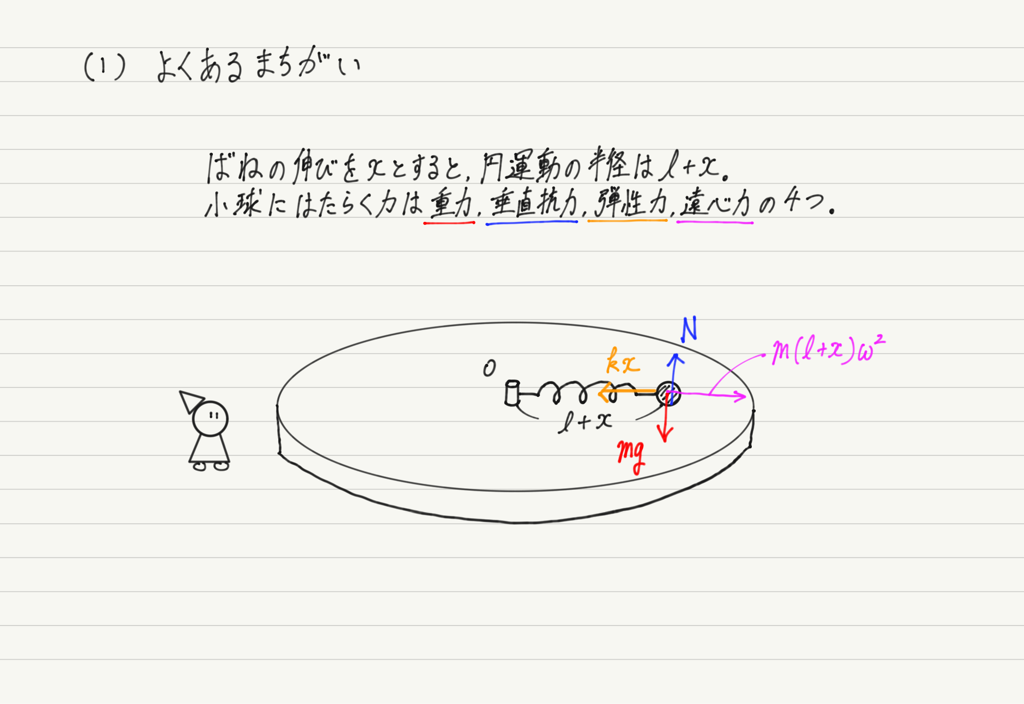
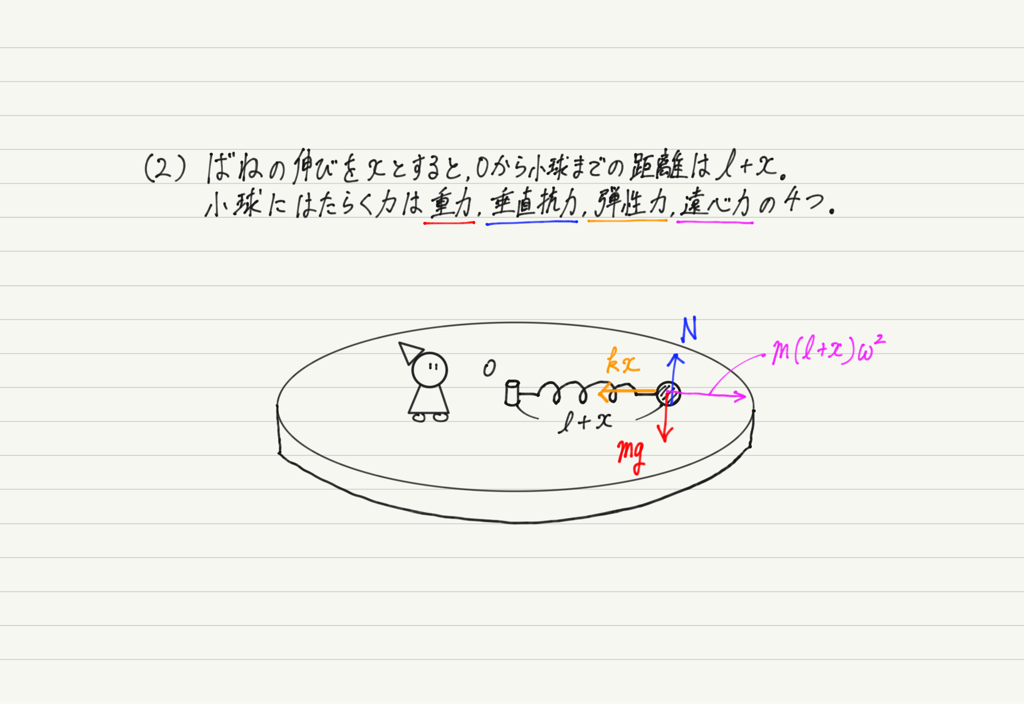
まずは(1)。 力学の問題なので,あれこれ考える前にまずは小球にはたらく力をすべて書き込みます。
正解の前によくあるまちがいを共有しておきましょう。
どこがまちがっているかというと,遠心力です。
先ほど述べたとおり,遠心力というのは円運動している人だけに存在する力です。
(1)の問題文を読むと,台の外で静止している観測者の立場から問題を解けと言われているので,この問題では遠心力を書き込んではいけません!
正しい解答は↓
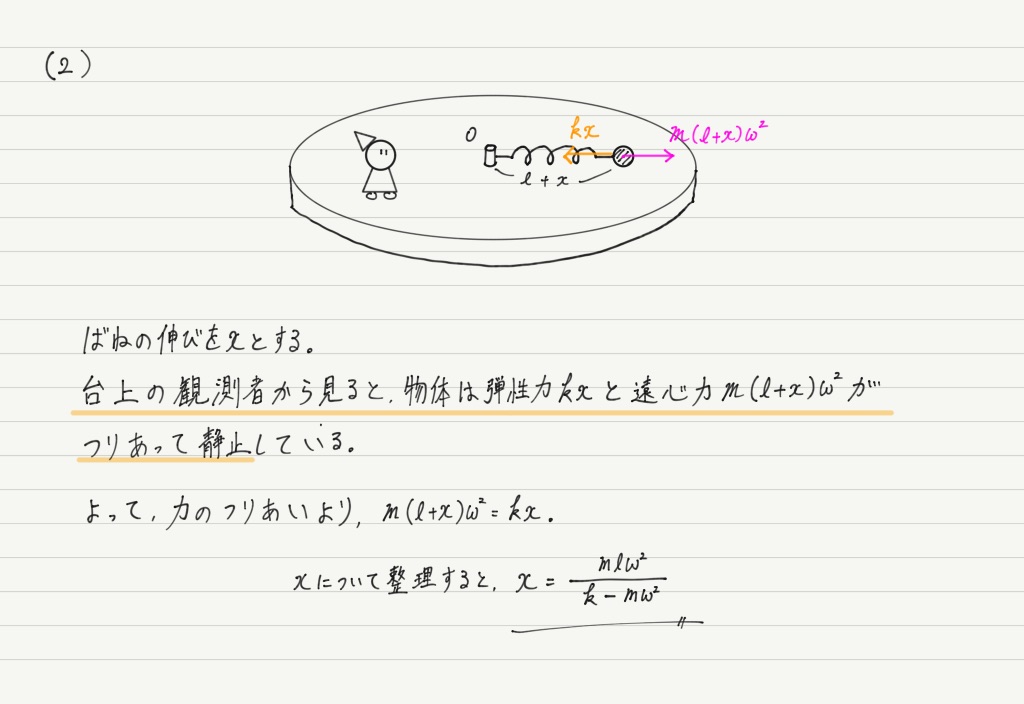
続いて(2)。 今度は観測者も台に乗って円運動しています。
すると(1)とは状況が変わりますね?
この観測者は遠心力を実感しているはずなので,今度こそ遠心力を書き込みます。
ところで,(1)と(2)のちがいは遠心力の有無だけではありません。 何かわかりますか?
答えは「小球の運動の見え方」です!
(1)では観測者は台の外にいたので,小球は台と一緒に円運動していました。
ですが(2)では観測者は台に乗っています!
この観測者から見ると回転しているのは周りの風景であって,同じ台に乗っている小球は静止しています!
静止しているのだから,この観測者が立てるべき式は力のつりあいの式ですよね!
(1)と(2)で立てた式を見比べてください。
(1)は運動方程式,(2)は力のつりあいの式なので,式の “意味” はちがうけど,式の “形” は同じです。
結局,観測者が静止していても円運動していても,それぞれの立場で正しく解釈して正しい式を立てれば,どちらの立場を採用しても同じ結果が得られることになります。
どちらの立場でもしっかり計算できるように,「現象を見る目」を養っておくことが大切です!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
余談:遠心力を使う?
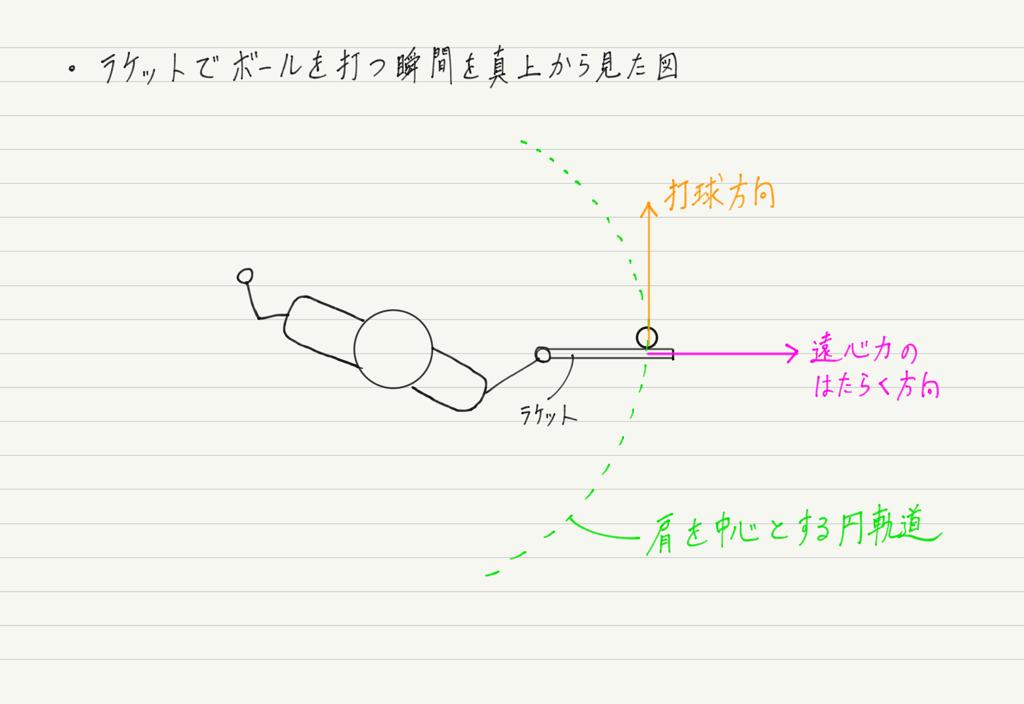
野球やテニスをやっている人,打つときに「遠心力を利用して打て」というアドバイスをされたことありませんか?
これってよく考えるとおかしいですよね?
何がおかしいかは,打球の向きと遠心力の向きを考えればわかるはずです。
ほら!
打球方向と遠心力は直角なんだから,打球の威力を上げるのに遠心力は利用できません!
この話に限ったことではありませんが,科学用語を使われるとそれっぽく聞こえるけど,よくよく考えると意味不明ってことはよくあります。
だまされないようにしっかり勉強しないといけませんよ!
次回予告
円運動の話題はこれでおしまいですが,次の運動に入る前に,見かけの力についてもう少し理解を深めましょう!