今回から本格的に加速度運動に入ります。 等速直線運動では味気ないから，速度が変化する運動を扱おう！
という話ですが，速度がデタラメに変化するような運動だとさすがに扱うのが大変そうなので，高校物理では等加速度運動を扱うことになります。
等加速度運動とは
前回，単位時間あたりの速度変化を表す量として「加速度」を定義しました。
等加速度運動とは加速度が一定の運動，つまり，速度が一定の割合で増えたり減ったりする運動のことです。
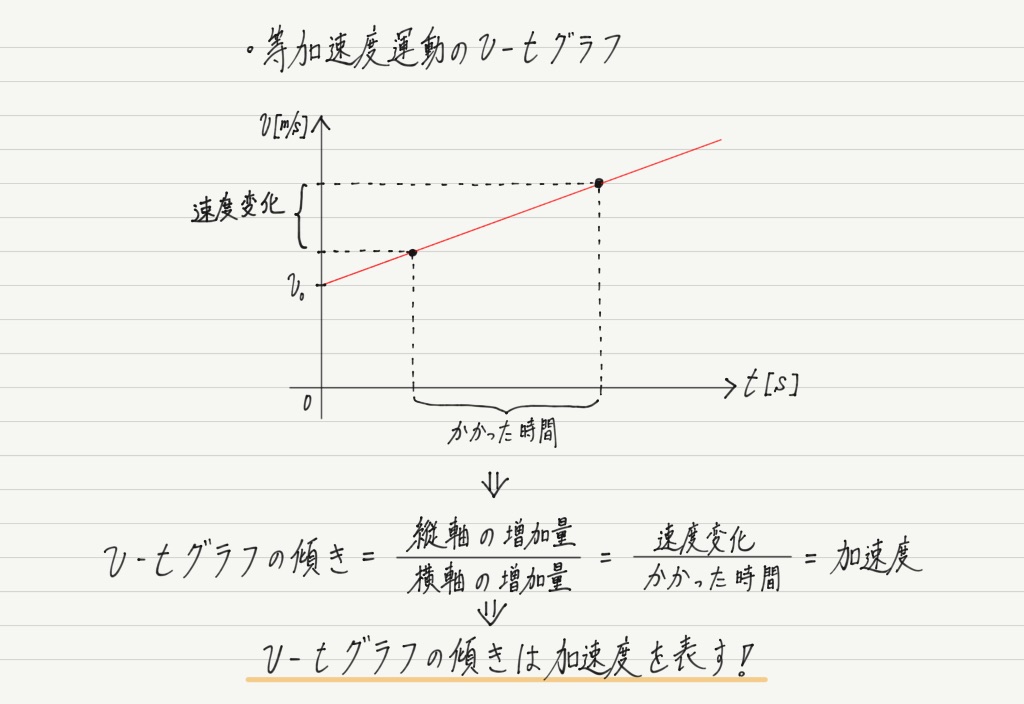
速度の増え方（または減り方）が一定なので,等加速度運動のv-tグラフは下図のような直線のグラフになります。 ポイントはグラフの傾き！
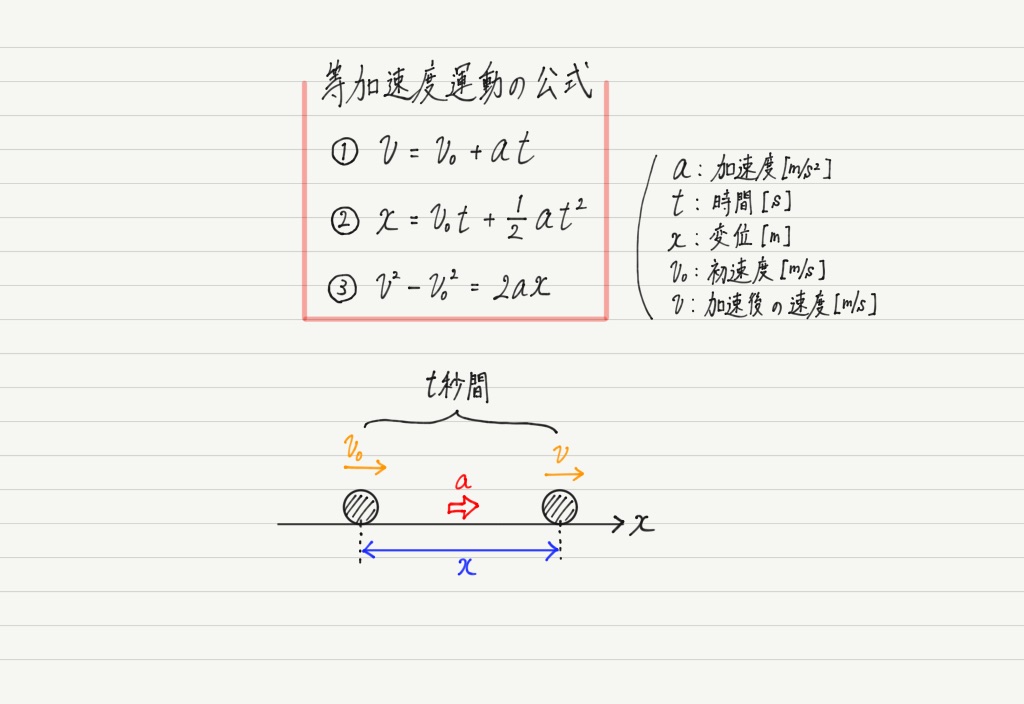
等加速度運動の３つの公式
ここでの目標は加速度運動している物体の様子を知ることです。 具体的には，スタートしてから10秒後の速度や位置を求めたり，20m進むのにかかる時間などを求めます。
等速直線運動とはちがって速度が変化するので難しそうですが，これらを求めるための公式があるので紹介します！
…出てくる文字も多いし，長めの式もあるし，正直覚えにくい公式だと思いますが，がんばって覚えましょう！！
以下では，この３つの公式がどこから出てきたのかを説明します。
等加速度運動の式の導出
まず公式①ですが，前回出てきた加速度の式を変形しただけ。
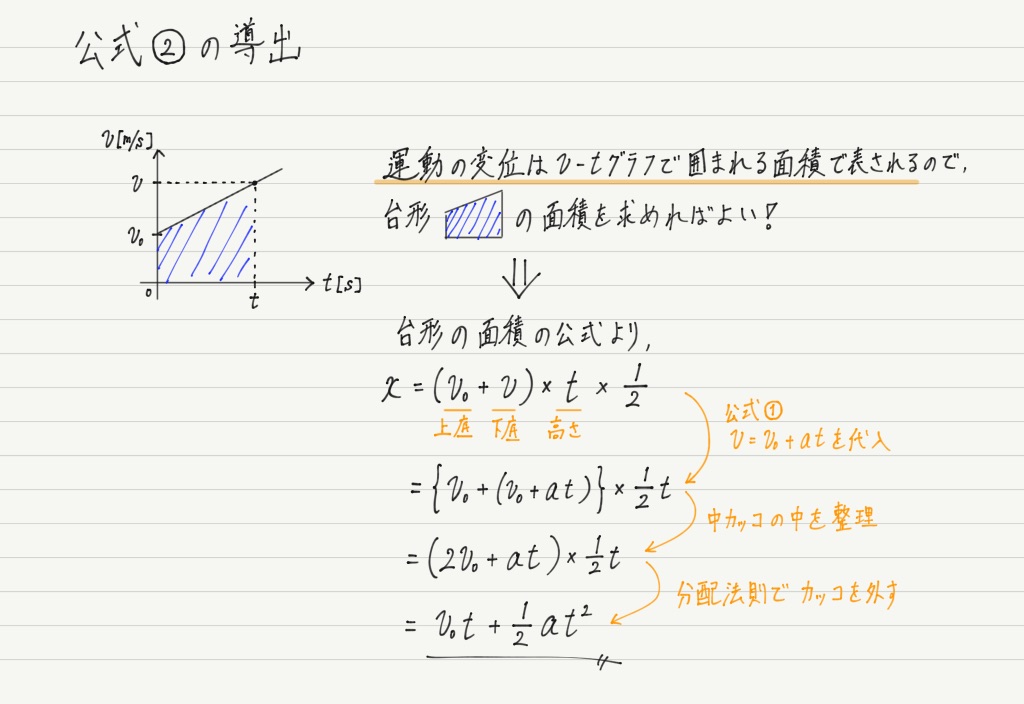
続いて公式②。 これは変位xを求める式ですが，一筋縄ではいきません。
以前やった「v-tグラフの囲む面積は距離を表す」という事実を用います。
忘れている人は以下の記事参照。
このグラフの面積の話は，等速でない運動でも成り立ちます！
まさかこんなところでで台形の面積を求める公式に出会うとは思わなかったでしょう！笑
知識はどこで役に立つかわからないものです。
さて，最後に公式③ですが，これは公式①と②を連立して得られます。
具体的には公式①をt = …の形に式変形して，それを公式②のt に代入すればOK！
…なのですが，代入した後の計算が面倒だし，この計算が特に大事なわけではないのでパス。 気になる人は教科書を参照してください。
（よくわからなくても気にしないこと。 公式③の導出がわからなくても物理の問題を解くのに支障はありません。）
このようにして公式①〜③が導かれます。 できれば公式の求め方もマスターしてほしいですが，現実問題として毎回自分で公式を導くのは大変なので，必要なときにすぐ使えるようにちゃんと覚えておきましょう。
それから実際に公式を使って問題を解くときは，３つのうちどの式を使うのかというのも大事な要素です。 まとめノートに使い分けのヒントを記しておきます！
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
まだまだ等加速度運動は続きます。 次回の記事を読む前に公式をしっかり覚えておいてください！！
