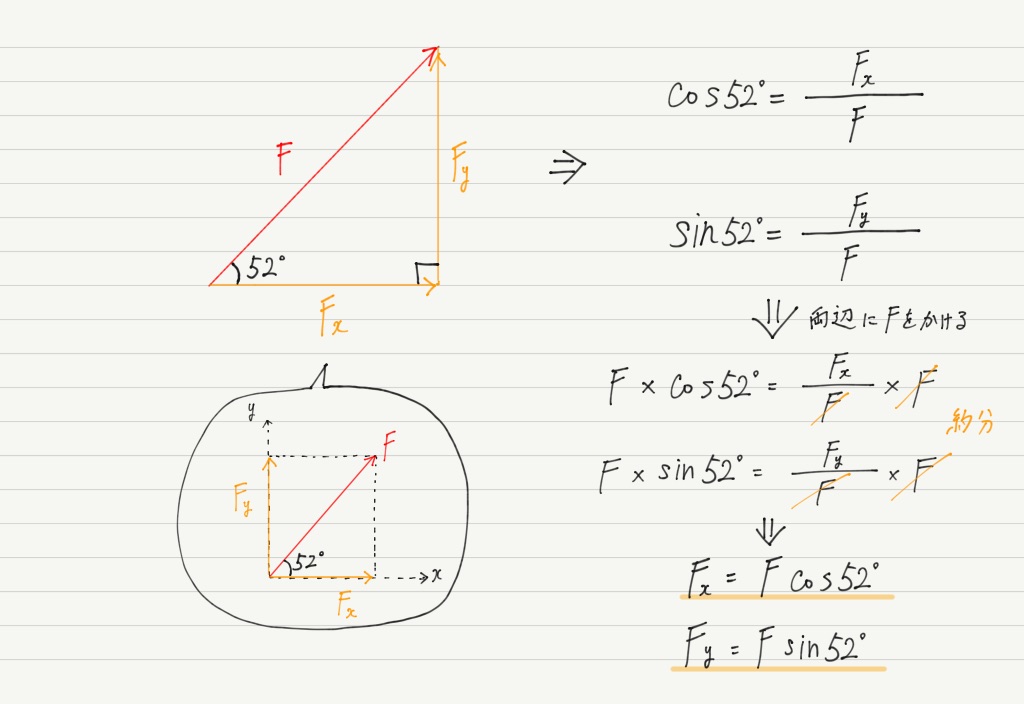本編で力の分解を扱ったとき,分力の大きさは直角三角形の辺の比を用いて計算していました。
しかし,辺の比が分かるのはせいぜい30°,45°,60°くらいで,それ以外の角度は分かりません。
そこで今回は,どんな角度の場合にも使える分力の求め方をお教えします!
三角比を使って分力を求める
どんな角度であっても分力を求める方法,それはズバリ「三角比の利用」です!!
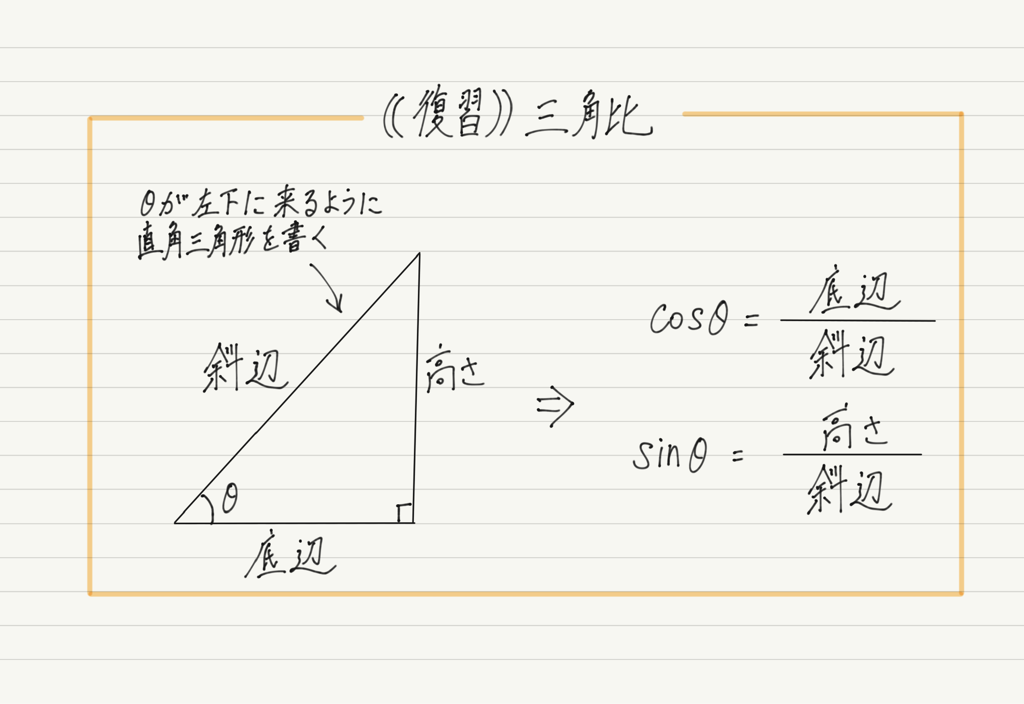
利用,といっても難しい応用ではありません。 まずは三角比のおさらいから。
力の分解の図にこれをあてはめて式変形すれば,x成分,y成分が得られます。
適当な角度の三角形を使って実際にやってみましょう。
52°の三角形の辺の比なんて分かりませんが,sin52°,cos52° の値なら計算機に打ち込めばすぐ求められます。
もちろん52°というのは1つの例であって,他のどんな角度でもsin,cosを斜め方向の力にかけることで分力を求めることが可能です。
どっちがサインでどっちがコサイン?
力の分解はいつも水平方向と鉛直方向への分解とは限りません。
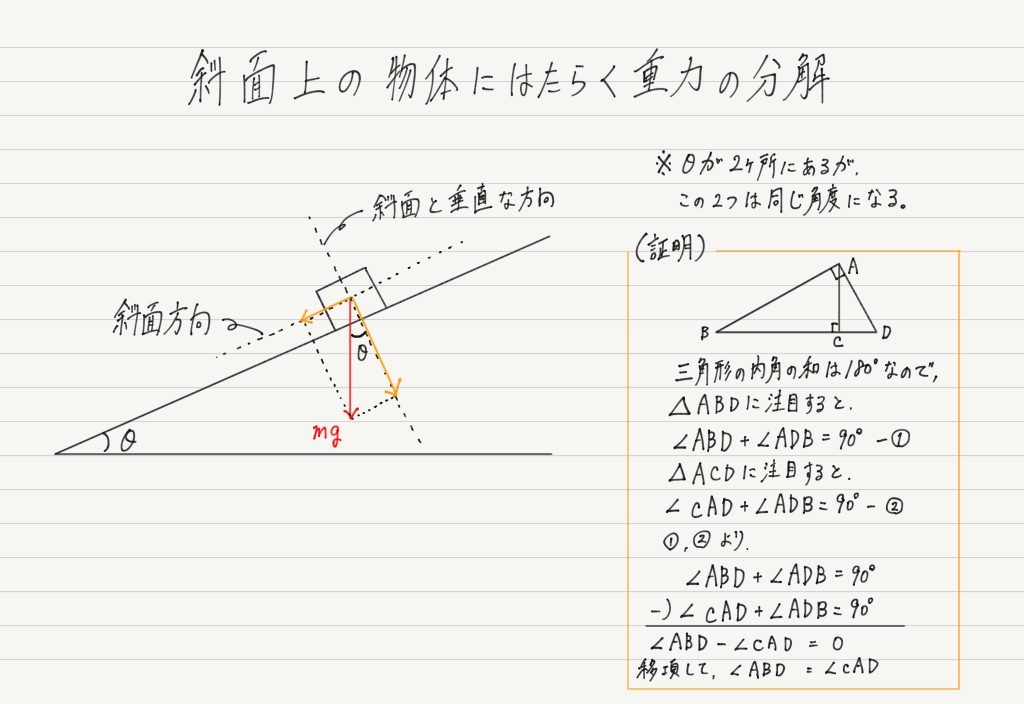
たとえば斜面上の物体にはたらく重力は,斜面方向とそれに垂直な方向に分解します。
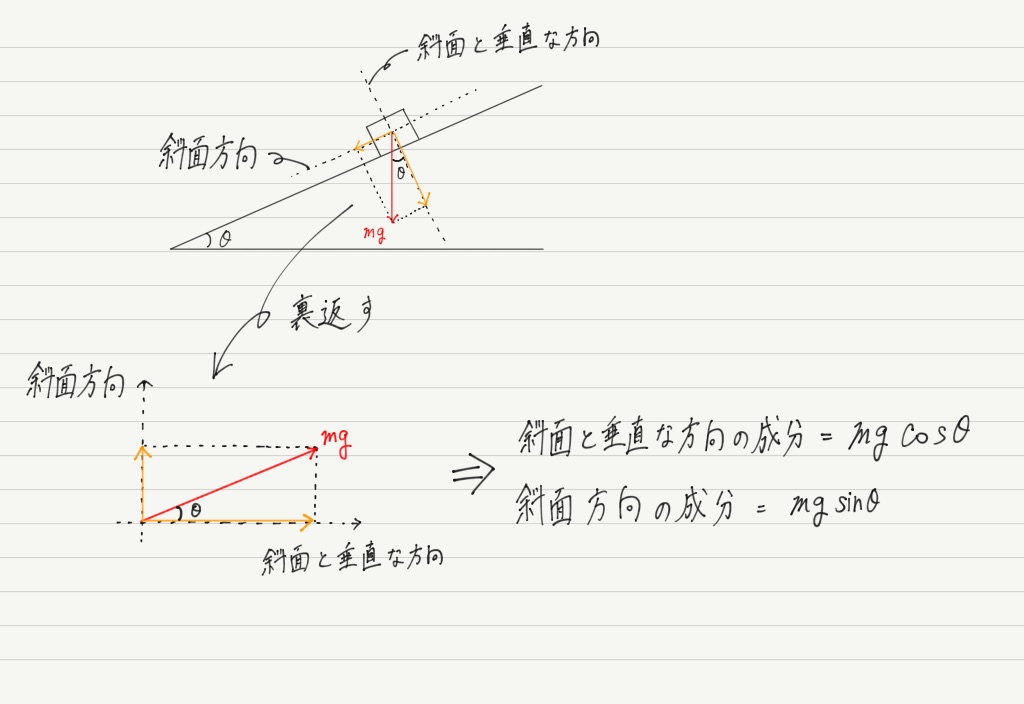
さて,分力を求めるには 元の力mgにsinθかcosθをかければいいわけですが,斜面方向とそれに垂直な方向,どっちがmgsinθで,どっちがmgcosθかすぐに判断できますか?
もちろん三角形の向きを変えて考えれば分かります。
しかし,いちいち向きを変えて考えるのも面倒です。 何か規則性はないのでしょうか?
それを見つけるため,いくつか例題をやってみましょう!
まずは自分で考えて,答えを出してから続きを読んでください。
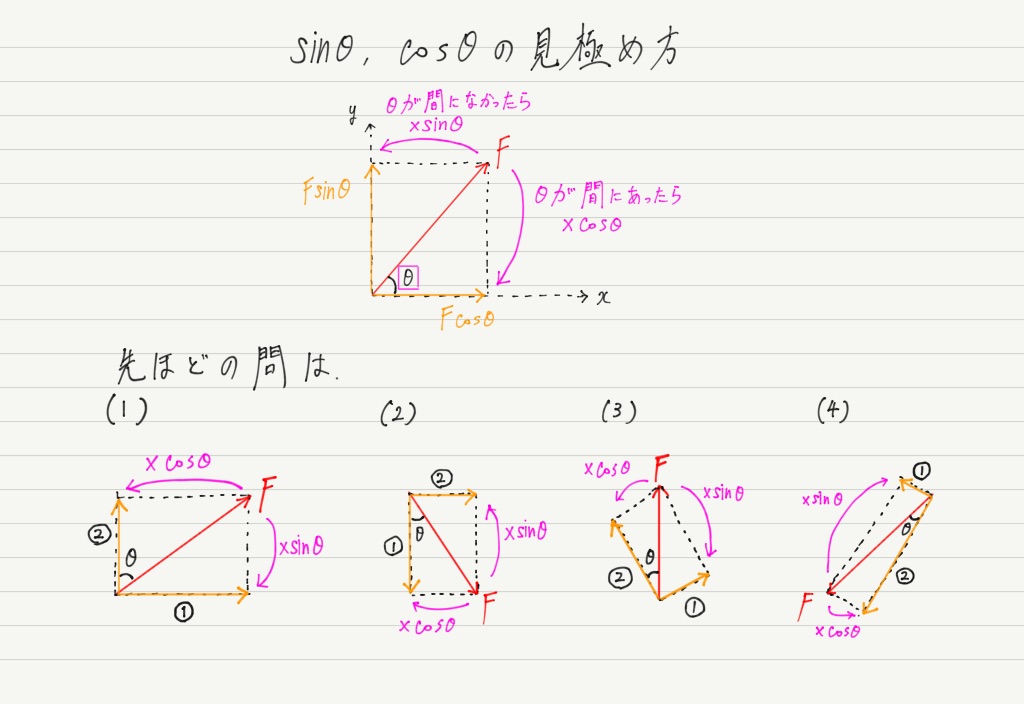
問の答えは,(1)② (2)① (3)② (4)② です!
さて,Fsinθと Fcosθの規則性はわかりましたか?
実は,こうやって簡単に見極められます!
これを押さえておけばいちいち三角形を書いたり,向きを変えたりしなくていいので楽チンです!
ぜひマスターしてください!
今回のまとめノート
三角比が出てくると拒否反応を示す人が多いですが,実際はそんなに難しいものではありません。
たくさん問題を解くうちに慣れるものなので,三角比が登場する問題も毛嫌いせずにどんどん挑戦してください!