子どもの頃シャボン玉をつくって遊んだ記憶は誰にでもあると思います。 きれいに色づいて見えるシャボン玉ですが，色づいて見える理由は光の干渉です。
今回は干渉の総仕上げとして，シャボン玉が色づいて見える条件（＝シャボン玉によって光が強めあう条件）を導出してみましょう！
距離の差を求める
前回のくさび形空気層が，“薄い空気の層”による光の干渉だったのに対し，シャボン玉の場合は“薄いシャボン液の層”による光の干渉です。
シャボン玉に限らず，薄い膜状の物質（＝薄膜）は光の干渉を引き起こします。
では薄膜による光の干渉条件はどのようになるでしょうか？
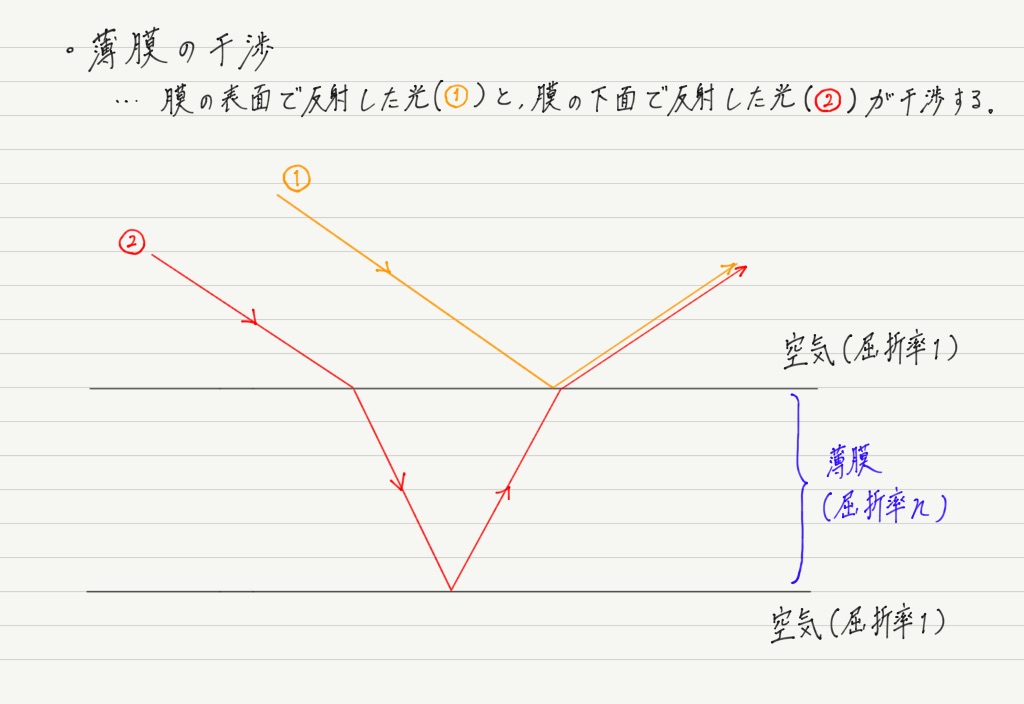
くさび形空気層では，空気層の上面で反射する光と，下面で反射する光が干渉しましたが，薄膜も同様です。 まずは光線の経路を作図してみましょう！
干渉条件を得るために，まずはいつもどおり光線①と②の距離の差を求めてみましょう。
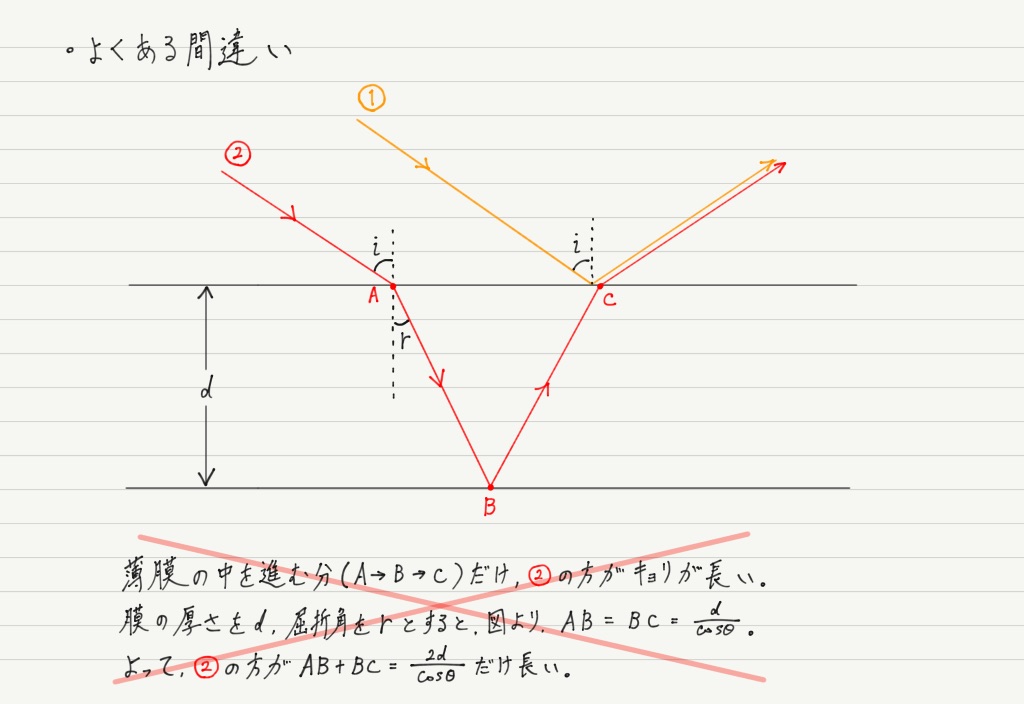
正しい計算の前に，この距離の差を求める際のよくある間違いを紹介します。
この間違いの原因は，薄膜へ光が入るタイミングの差を考慮していないこと。
光が斜めに入射しているため，薄膜に到達するタイミングが①と②で異なっていることに気づきましょう！
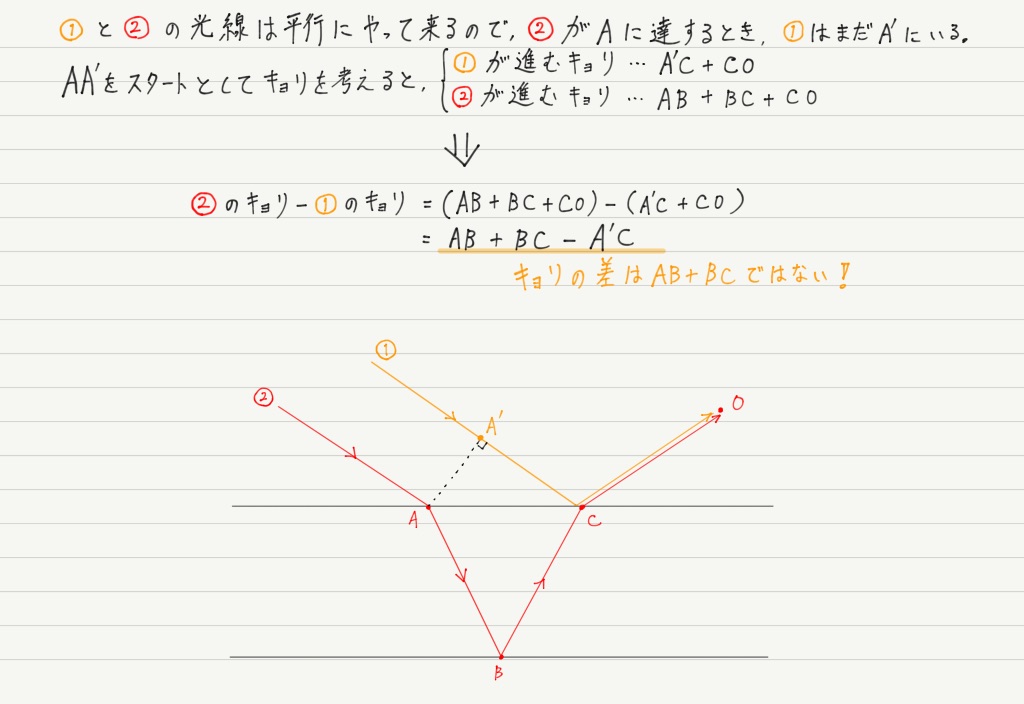
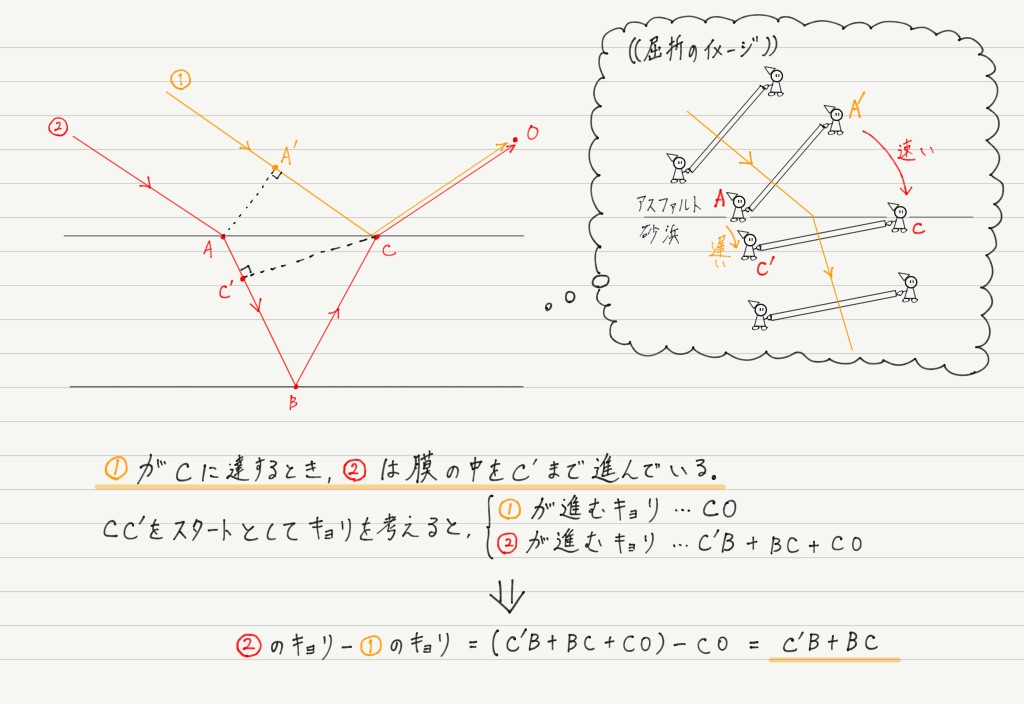
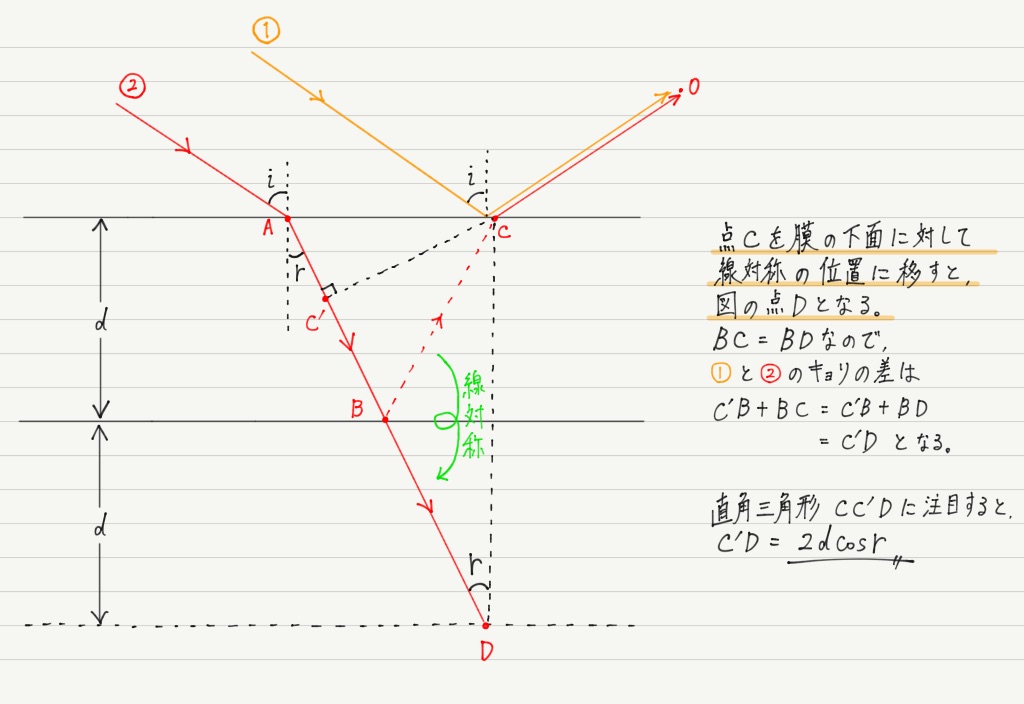
距離の差を正しく計算するポイントは，①がCに来たときに，②はどこまで進んでいるかを考えることです。 物理基礎で解説した，屈折のイメージを思い出すとわかりやすいでしょう。
これで長さを求めるべき場所がわかりましたが，求めるためにはちょっとした工夫が必要です。
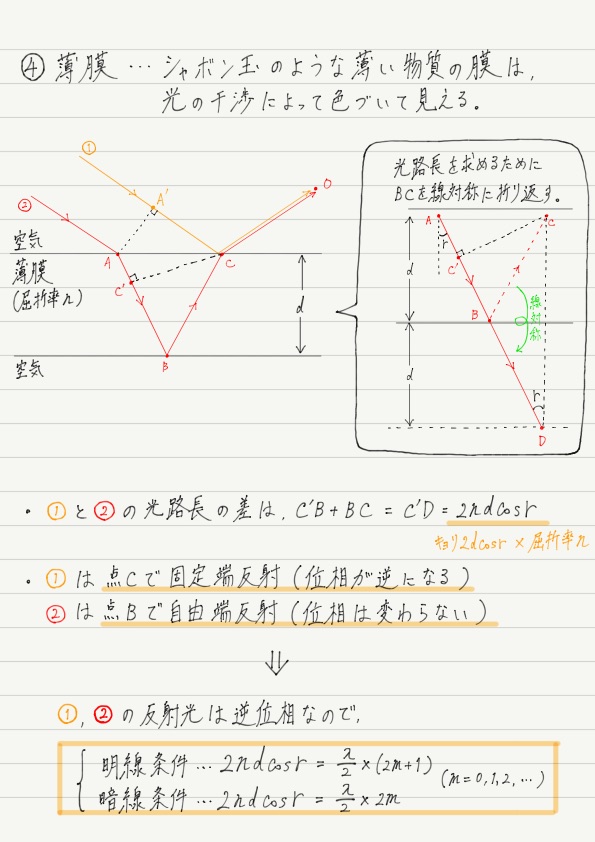
これで①と②の距離の差が求められました！
反射による位相の変化を考える
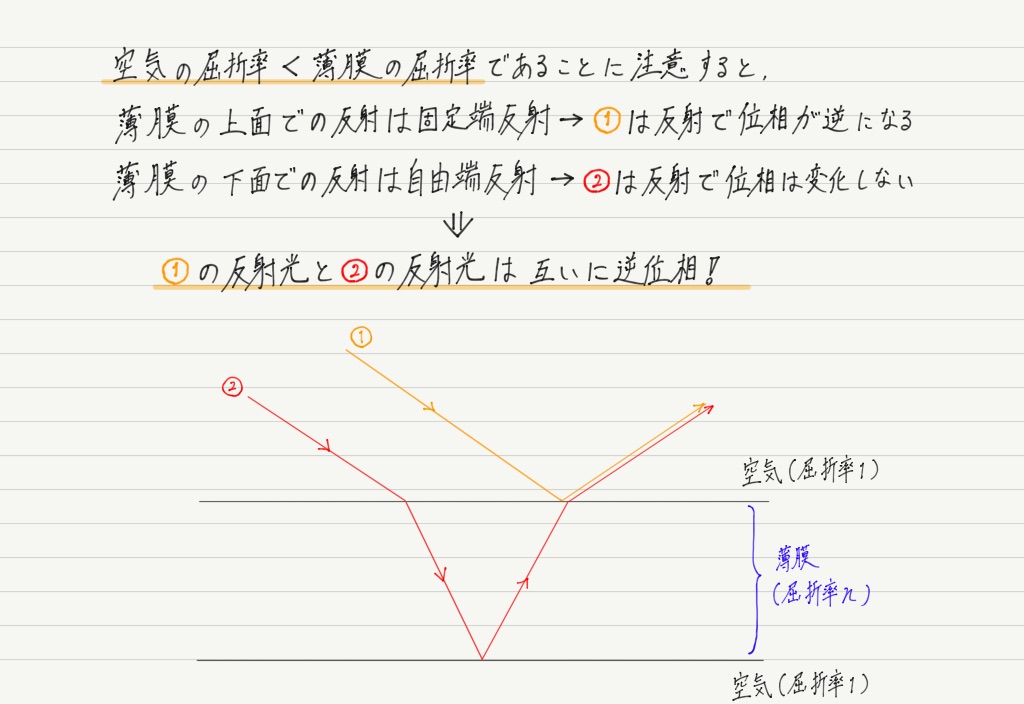
さて，前回のくさび形空気層同様，途中で光が反射しているので，反射による影響も考えなければいけません。
よって今回も逆位相バージョンの干渉条件が適応され，距離の差＝半波長 × 奇数で強めあい，距離の差＝半波長 × 偶数で弱めあうということになります！
これでおしまい…？
光路長という考え方
この干渉条件，実は最後にもう1箇所だけ手を加える必要があります。
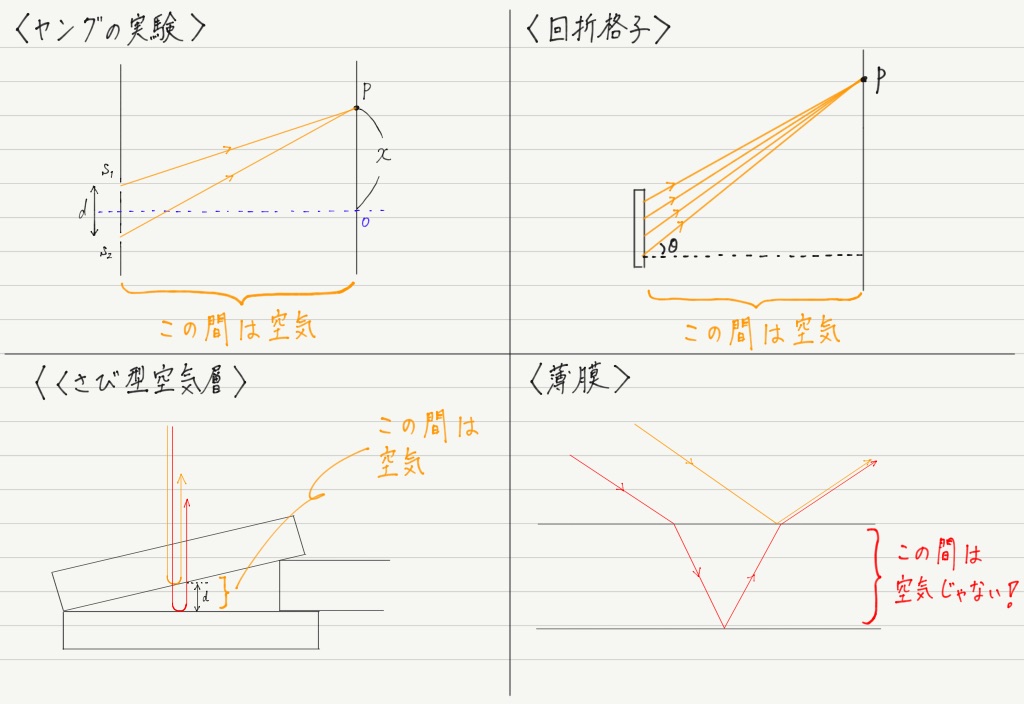
それは，これまでに習った干渉（ヤングの実験，回折格子，くさび形空気層）と薄膜の干渉の “あるちがい” に由来するのですが，一体何がちがうのか分かりますか？
答えは，「これまで習った干渉はすべて空気中で距離の差が生じているが，今回だけ物質（膜）の中で，距離の差が生じている」です！
光の干渉条件はこれまで「距離の差＝半波長 × 偶数（or 奇数）」としてきましたが，正確には「光が真空中（≒空気中）を進むときの距離の差＝半波長 × 偶数（or 奇数）」です（ “真空中を進むときの距離” のことを光路長という）。
今回の問題は膜の中で距離の差が生じているため，上で求めた2dcos r は干渉条件に使えないのです。
さて困った…(・・;)
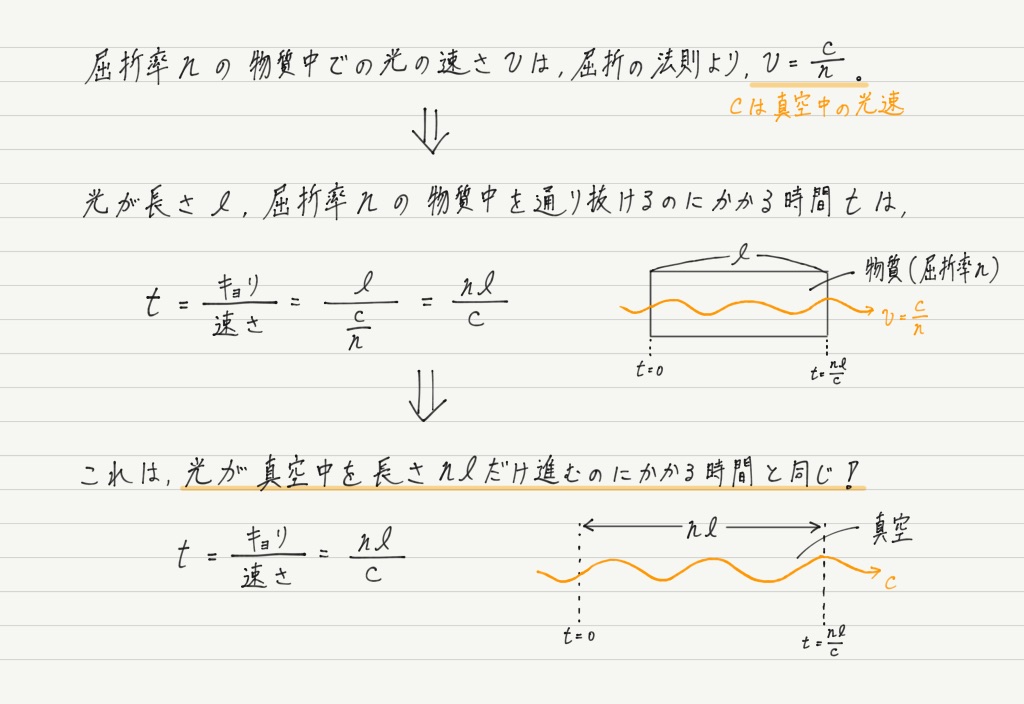
この困った状況を解決してくれるのが屈折の法則！
物質中での単純な距離（今回は 2dcos r）に物質の屈折率 n をかければ，光路長に早変わり！
ここまでの話をまとめると，薄膜の干渉では，2ndcos r = 半波長 × 奇数が明線条件で，2ndcos r = 半波長 × 偶数が暗線条件ということでファイナルアンサー（古い）でございます。
これで4パターンの干渉について解説が終わりました。 何度も言いますが，干渉条件をそのまま暗記しても通用しません！
与えられた設定から自力で求められるようにすることが大事。 干渉条件を求める手順について，最後にまとめておきましょう。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
この後は，もう一度このブログを読み直して復習するもよし，ハイレベルな問題集に進むもよし。 各自の目標に応じて，これからも波の勉強を続けてもらえればと思います。
読んでくださり，ありがとうございました。
