レンズがつくる像について理解を深めていきたいと思います。
前回は像の作図を学習しましたが,イメージで作図をしたわけではなく,ちゃんと「レンズを通る光の進み方のルール」に基づいて作図をしました。
明確なルールによって像が作図できるということは,像ができる場所や像の大きさは計算でも求められそうな気がしませんか?
レンズの公式の導出
実際に,レンズのつくる像は「レンズの公式」と呼ばれる公式を使うことで求められます!
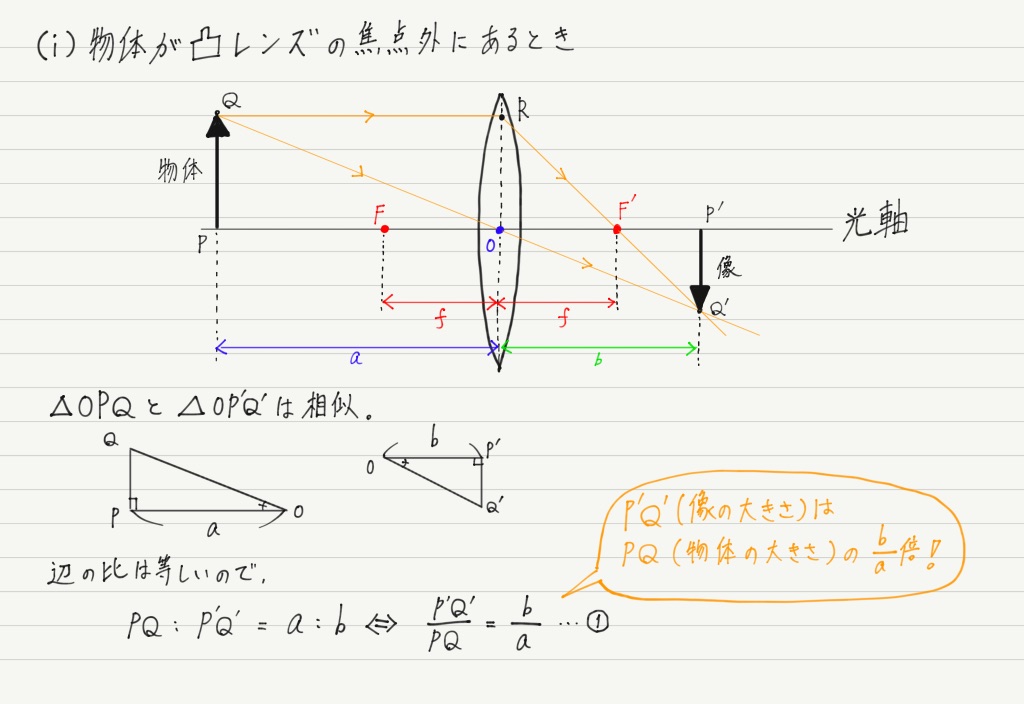
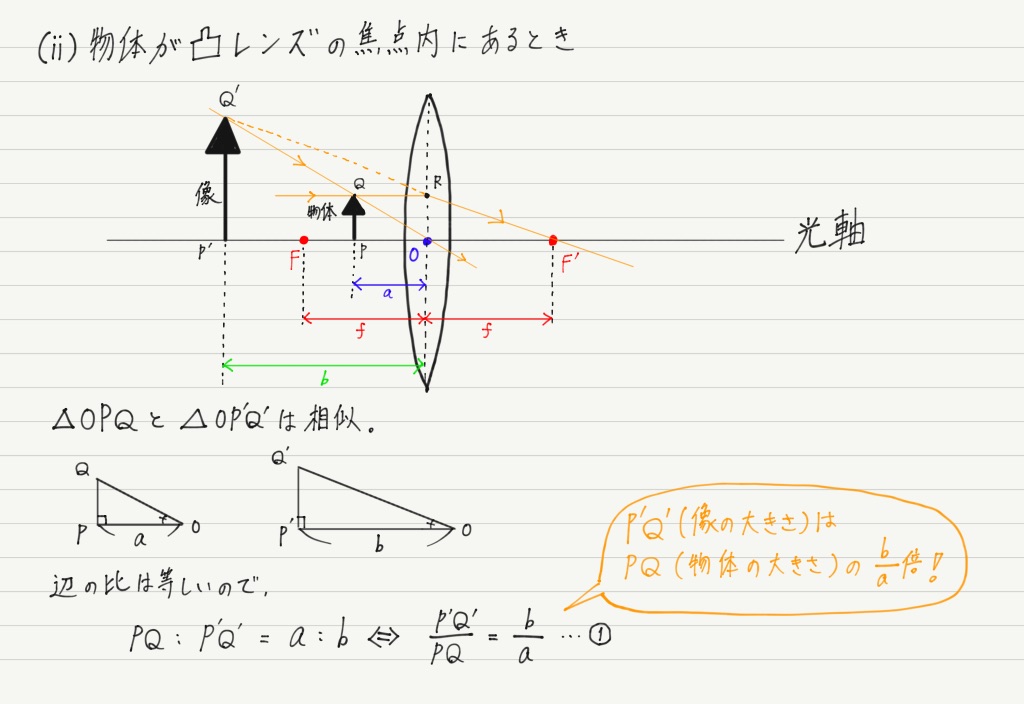
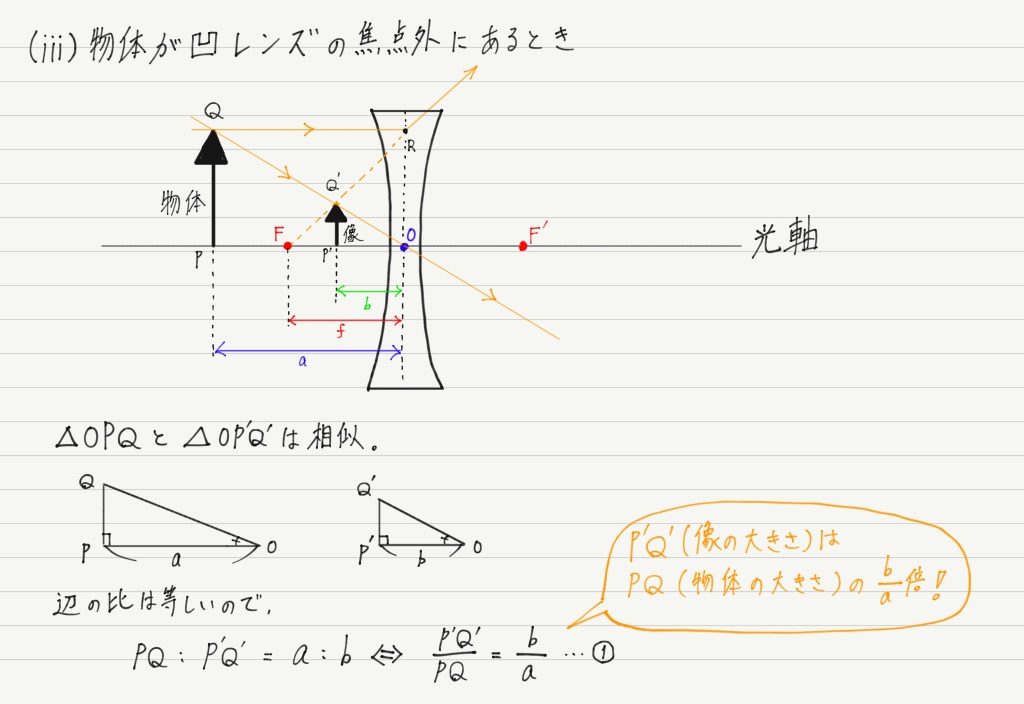
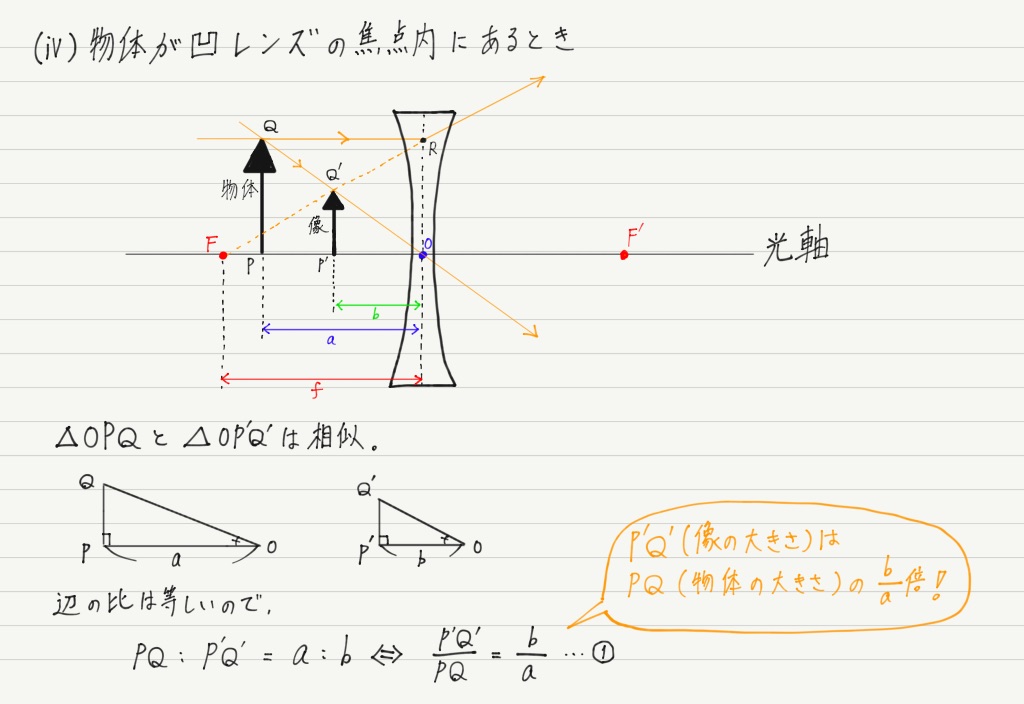
まずはレンズの公式をがんばって導出してみましょう。 導出には三角形の相似を利用します。
相似な三角形が大量に登場しますが,共通な角や対頂角に注目して「2組の角がそれぞれ等しい」を用いれば,相似であることはすぐに確認できると思います。
これでレンズの種類と物体の位置の全パターンを網羅したことになります。
この4つの式は形は似ていますが,ところどころ符号が異なっているのでこのままでは覚えにくい…。
もう少し詳しく考察してみましょう!
出てきた式を整理する
符号の付き方に何か規則性はないか探ってみましょう。
…と,その前に,式の形がコロコロ変わるのはすごく覚えにくいので,まずは小細工。
符号のちがいをこのように捉えると,残る問題は「文字が負になるのはどのような場合か」だけです。
それを考える前に,すでにお気づきの人もいると思いますが,凹レンズの式は物体の位置が焦点より外側でも内側でもまったく同じ式です!
同じ式なら分けておく必要はないので,ひとつにまとめてしまいます。
これで式は3本になりました。 いい感じ!
それでは本題。 符号が何で決まっているのか考えてみましょう。
だいぶ整理できたので,まとめておきましょう。
今回のまとめノート
先ほどやったように,レンズの公式は図を書いて相似比を使えば,自力で導出することも可能です。
…が,問題を解く度にいちいち導出するわけにもいかないので,公式をしっかり覚えてほしいと思います。
ところで,レンズの公式のことを「写像公式」と呼ぶ人がいます。
字面と響きはかっこいいですが個人的にこの呼び名はオススメしません。
「写像」という単語は,数学では特別な意味をもっているからです。
数学と物理で分野がちがうので意味を混同することはまずありえませんが,用語の濫用はよくないなーと思うのでみなさんはレンズの公式と呼ぶようにしてください!
例題
式に代入するだけの簡単な問題ですが,練習だと思って解いてみてください。
では,解答です。
レンズの公式のいいところは,数値を入れてしまえば像に関する情報がすべて機械的に計算できてしまうところです。
像ができる場所も,像の種類も,答えのbの符号を見れば一発。
いちいち「あれ?像はどこにできるんだっけ?実像?それとも虚像?」などと考える必要はありません。
こちら↓にも演習問題を用意しているので,ぜひチャレンジしてみてください!
次回予告
波の分野は終わりが見えてきました。
最後にして最大の難関,光の干渉に関する分野に突入していきます。