前回学習した波の独立性とは,2つの波がぶつかった後,お互いに影響を及ぼさずに素通りしてしまうことでした。
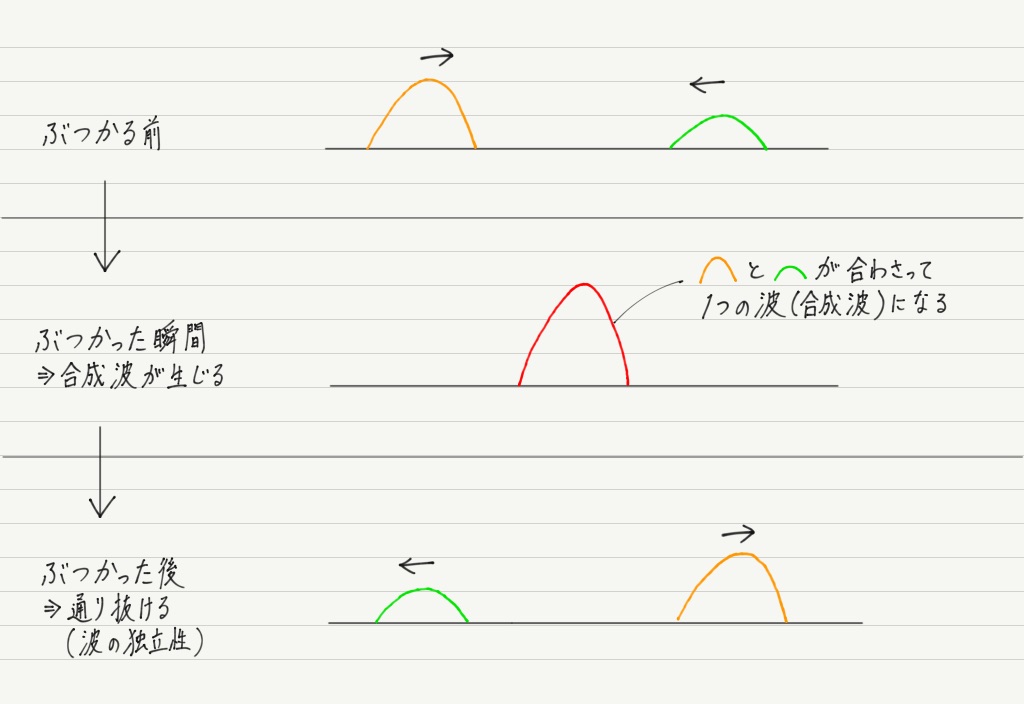
では,波どうしがぶつかった “後” ではなく,ぶつかった “瞬間” は一体どうなるでしょう? それが今回のテーマです!
波の合成
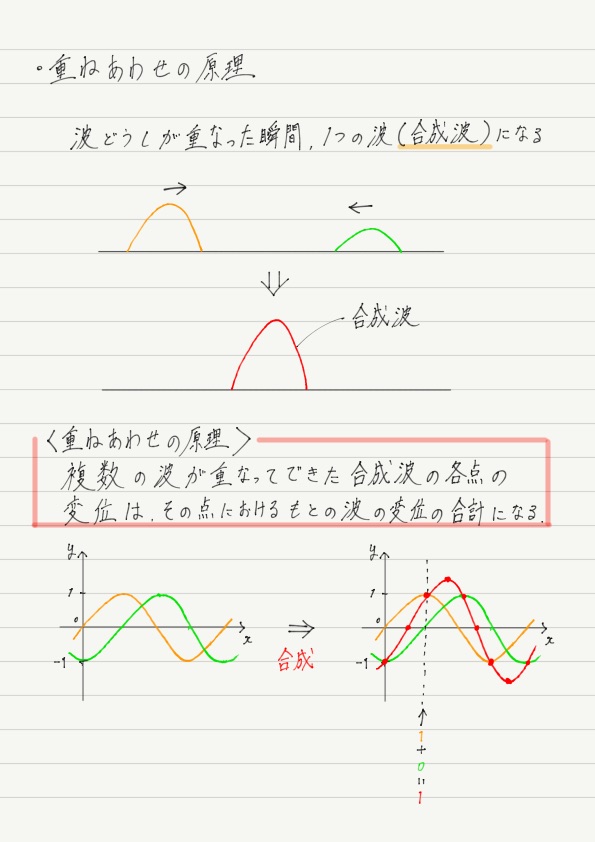
結論からいうと,ぶつかった瞬間,2つの波は重なって1つの波になります。 重なってできた波を合成波と呼びます。
さて,合成波の波形は元の波の波形とどんな関係にあるでしょうか?
実はとってもシンプルな関係になることが知られています。
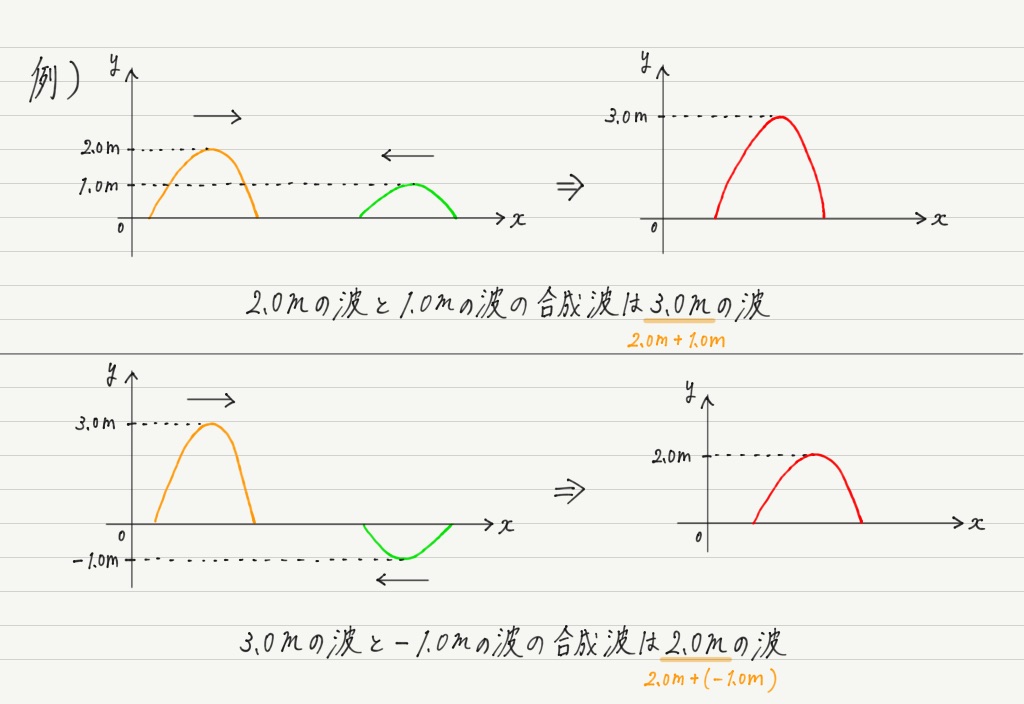
このように,合成波の変位は元の波の変位を足したものになります! すごく簡単ですよね!
このことを重ねあわせの原理と呼びます。
重ねあわせの原理はシンプルゆえにいろいろな応用が利きます。
たとえば1cmの波にー1cmの波をぶつけると,合成波の変位は1+(ー1)=0 となります。
これを利用しているのがヘッドホンのノイズキャンセリング機能。 周囲の雑音の波形を読み取り,それに対して逆位相の波をぶつけることで雑音を消しているのです。 なかなか賢い機能だと思いませんか?
合成波の作図
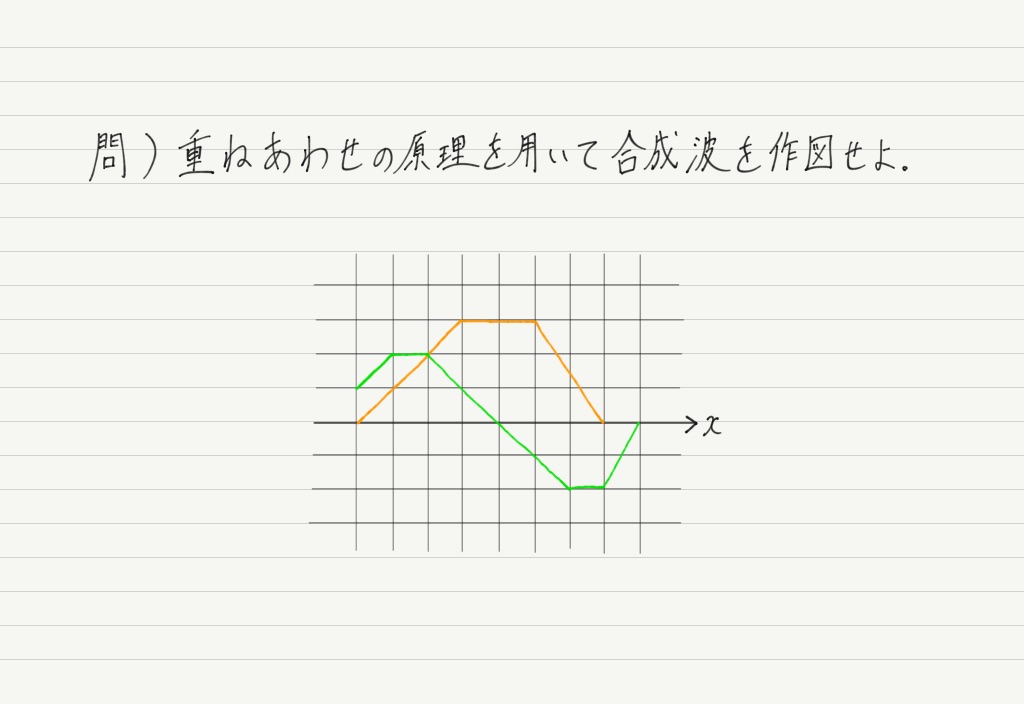
では,重ね合わせの原理を用いて合成波の作図をしてみましょう!
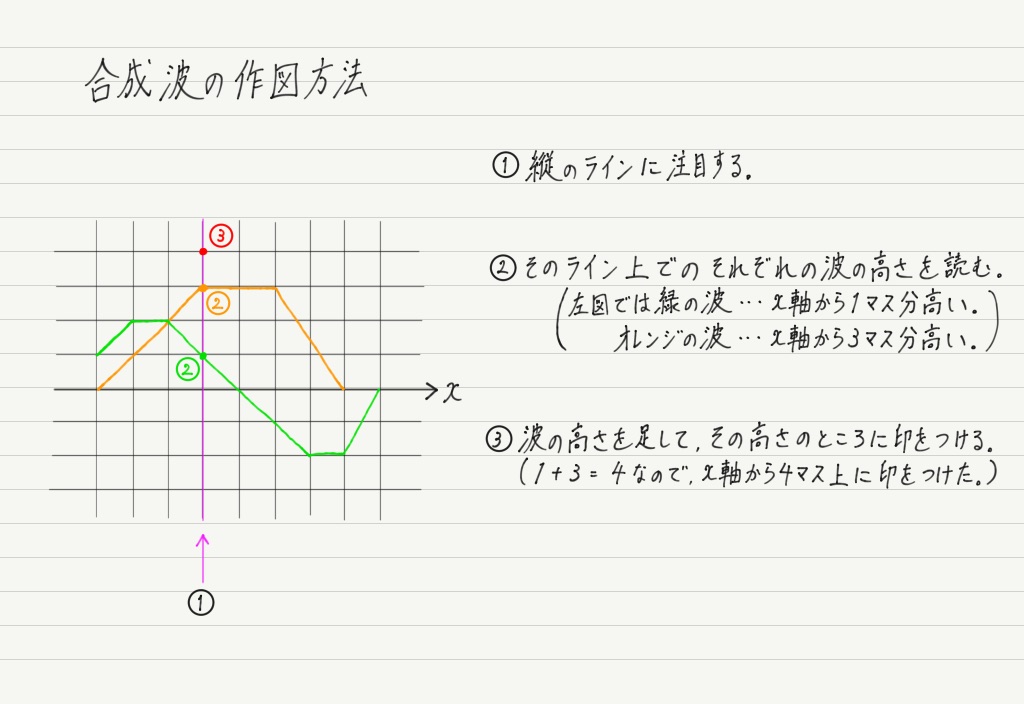
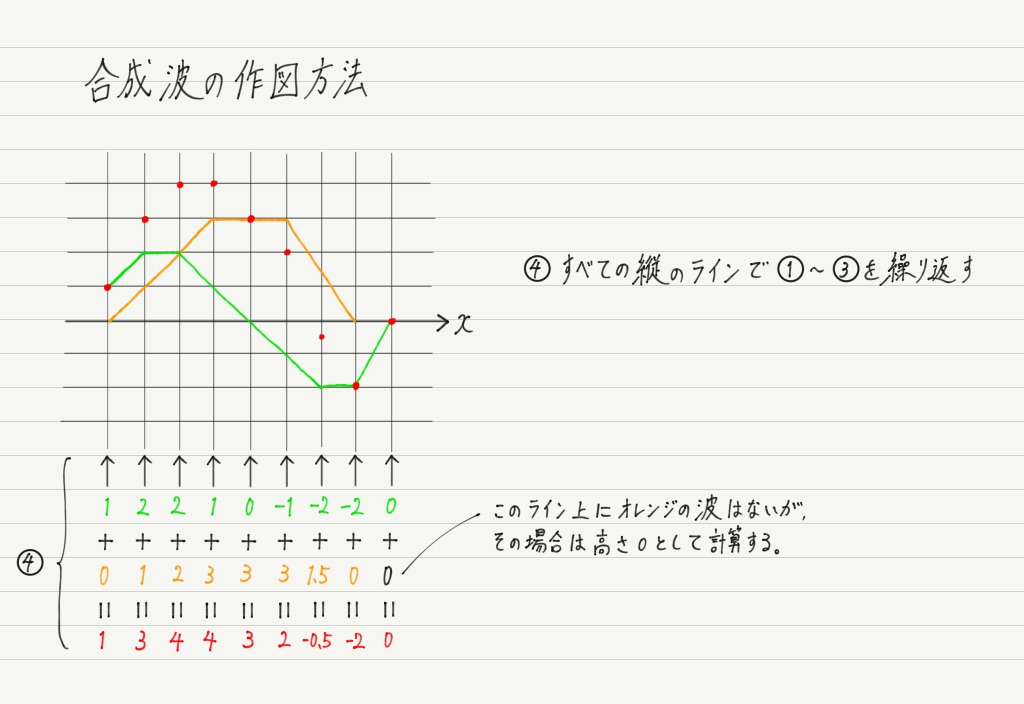
重ねあわせの原理を用いて合成波の高さを求めたいので,まずは縦のライン(x座標)ごとに2つの波の変位(高さ)を読み取って,それを足していきます!
足したらその値のところに印をつけましょう。
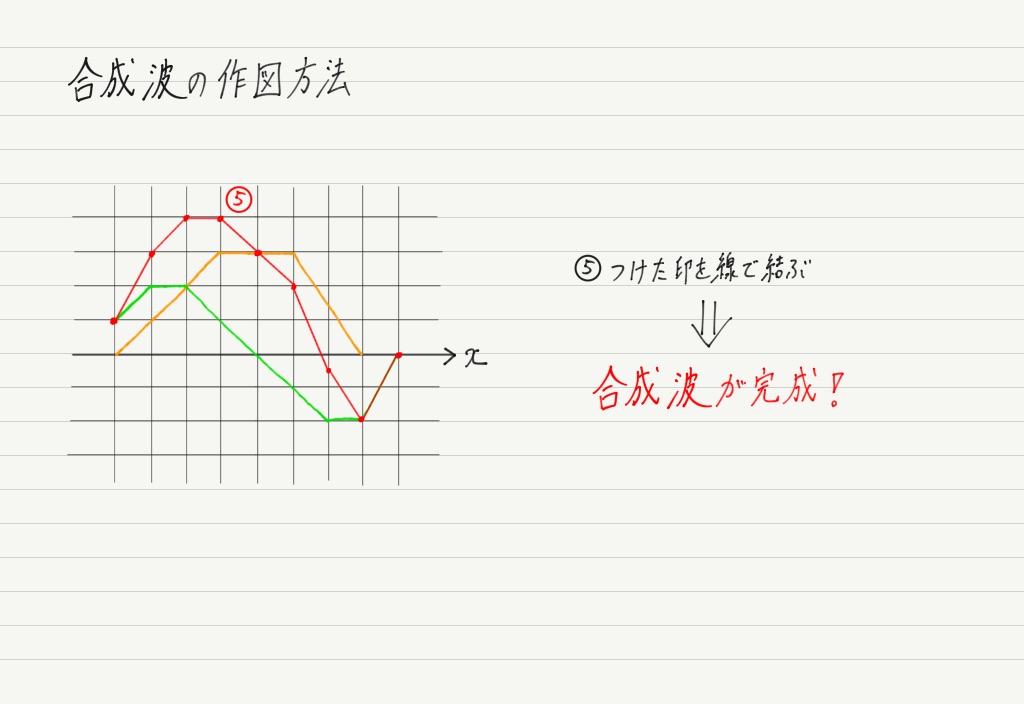
すべての箇所で印をつけ終えたら,その点をつなぎます。
つないでできた波形が合成波の波形です。 簡単な作図ですね!
点をつなぐときの注意点がひとつあります。
今回の問題のように,元の波が角張った形をしているときには合成波も角張った形になるので,点どうしは直線でつないでください。
一方,正弦波どうしを合成する場合,合成波は曲線になるので,点どうしはなめらかな曲線でつないでください(以下のまとめノート参照)。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は波の反射をやります!