今回は波の分野で頻出の用語たちをマスターしましょう!
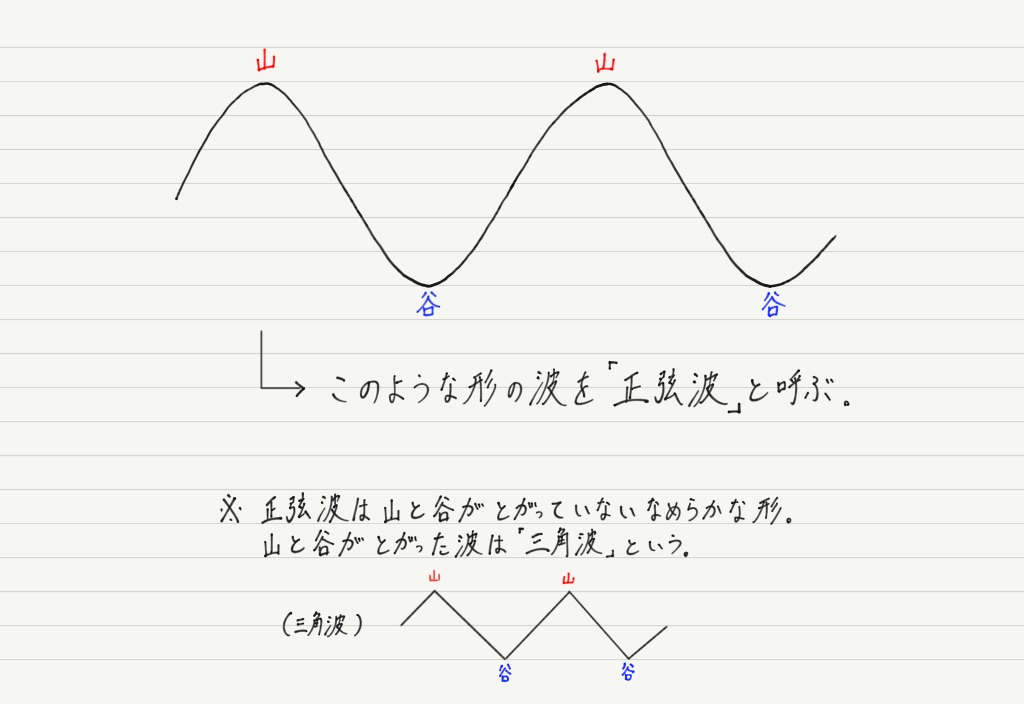
正弦波
高校物理では「正弦波」と呼ばれる,もっとも単純な波を扱うことがほとんどです。
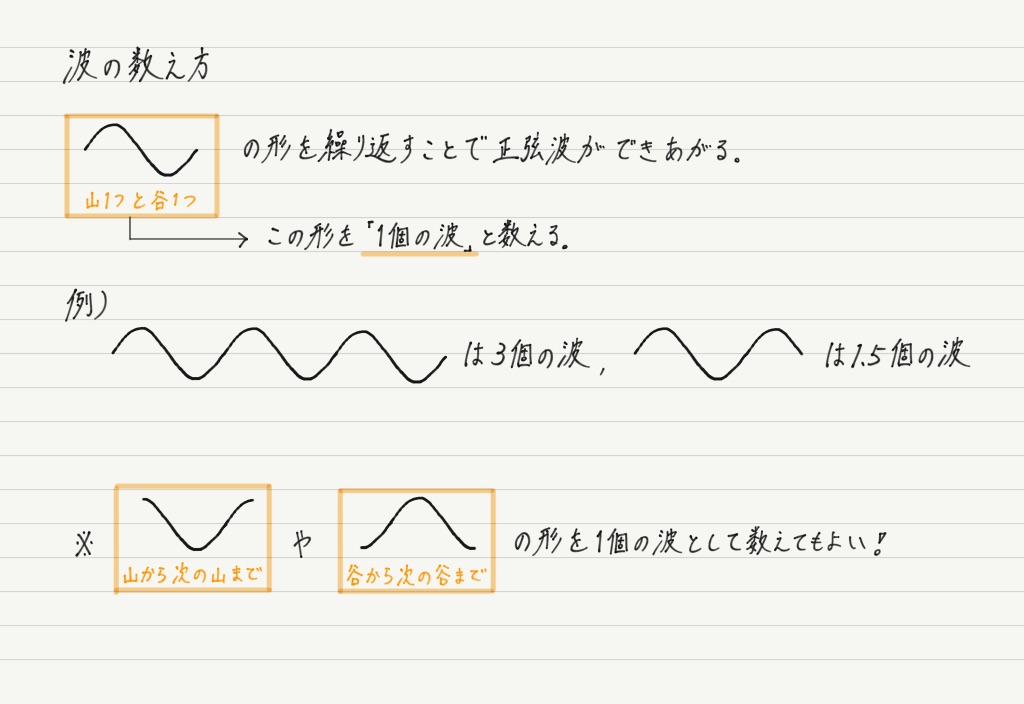
見てわかるように,正弦波は山の部分と谷の部分が交互に並んでいて,同じ形の繰り返しとなっています。 この「山と谷のセット」を何回繰り返しているかによって,「波◯個」と数えることにします(下図参照)。
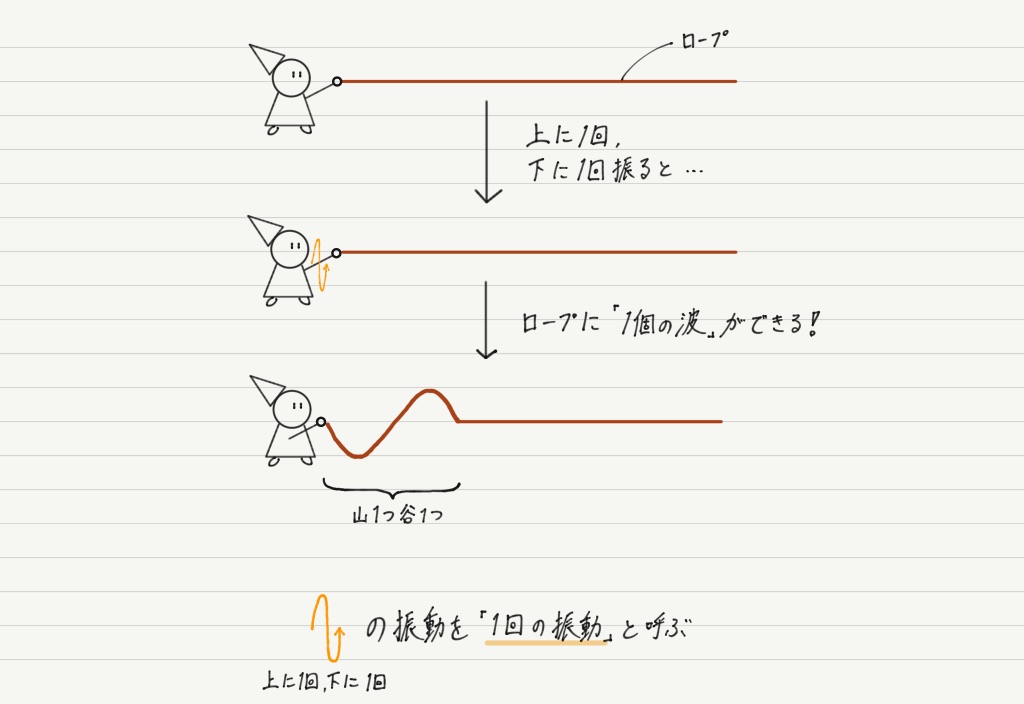
イメージをつかむために,ロープを伝わる波で考えてみましょう。
ロープの端を手で持って上下に振ると,ロープには正弦波が生じます。 ロープを振動させ続けると次々と波ができます。 このようにしてできた波を連続波といいます(途中で振るのをやめたものはパルス波という)。
また,ロープに1個分の波ができるような腕の振りを「1回の振動」と数えることにします。
周期
媒質を1回振動させるのにかかる時間を周期と呼びます(媒質という用語の意味がすぐに思い出せない人は前回の記事を見てください)。
上の例だと媒質はロープなので,
ロープをゆっくり振る → 長い周期
ロープを素早く振る → 短い周期
ということになります。
振動数
1秒間に媒質が振動する回数を振動数と呼びます。 再びロープの例で考えると,
ロープをゆっくり振る → 小さい振動数
ロープを素早く振る → 大きい振動数
ということになります。
周期と振動数の関係
上に書いたことをもう一度書いてみましょう。
ロープをゆっくり振る → 長い周期・小さい振動数
ロープを素早く振る → 短い周期・大きい振動数
周期と振動数の間になにか関係がありそうな予感…
そこで,もう一度定義を確認。
周期がT → 媒質が「T秒間」に「1回」振動する。
振動数がf → 媒質が「1秒間」に「f 回」振動する。
という意味です。 どちらも時間と回数がポイントなので,時間:回数という比をつくってみます。
周期がT → 時間:回数=T秒:1回
振動数がf → 時間:回数= 1秒: f回
どちらも同じ比を表しているので,
T:1=1:f
この式から,周期Tと振動数fの間にはfT = 1という関係が成り立つことがわかります。 この関係式は頻繁に用いるのでぜひ覚えてください!!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は波に関する計算をやっていきます!