今回も引き続きRLC回路の話題です。
直列だけやって並列をやらないのは気持ち悪いので,ちゃんと一度扱っておきましょう。
目次
RLC並列回路のベクトル図
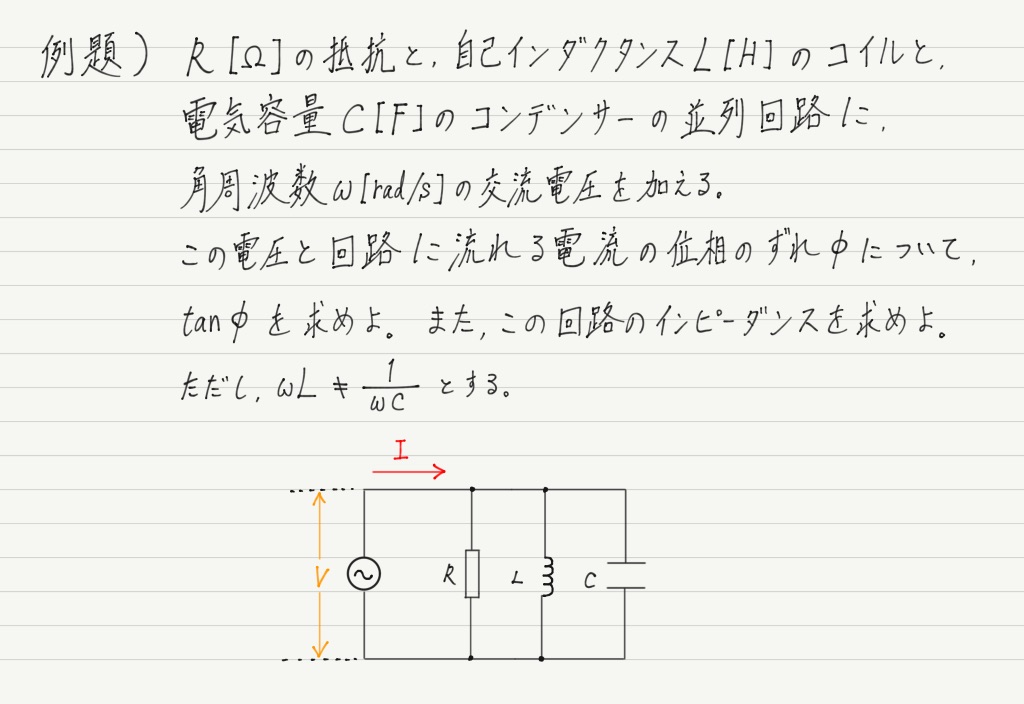
前回の例題の回路を直列から並列に置き換えて考えます。
これもベクトル図を使って簡単に解いていきたいのですが,まったく同様にとはいきません。
それは「位相の基準」の問題です。
直列の場合,R,L,Cで共通なのは電流。
そのため,電流を基準にして電圧の位相のずれを考えました。
ところが並列だと電流は途中で枝分かれしてしまうので,当然ながら電流はR,L,Cそれぞれで異なります。
じゃあ,並列回路で共通しているのは何…?
って,ヒント与えすぎか笑
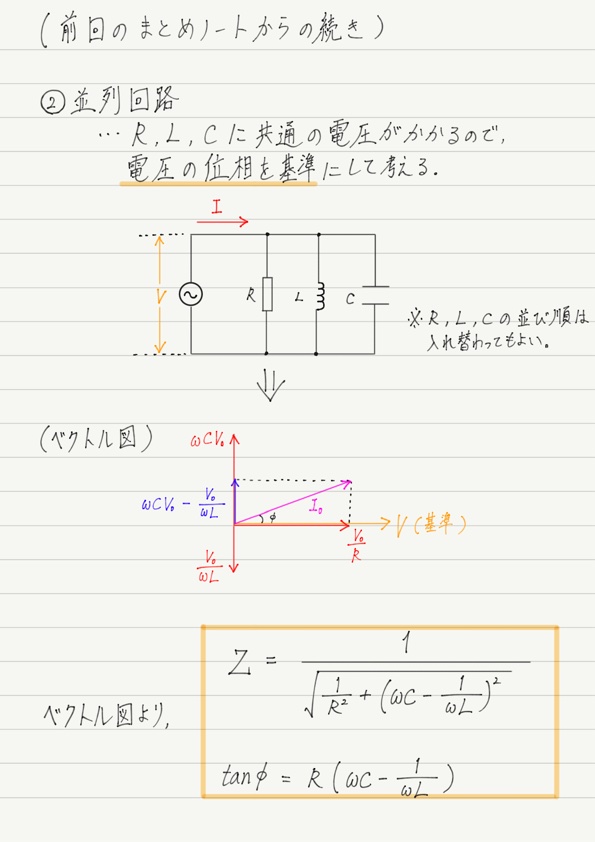
みなさん気づいていると思いますが,並列回路の場合はR,L,Cの両端にかかる電圧が共通してるので,電圧の位相を基準にして考えます!
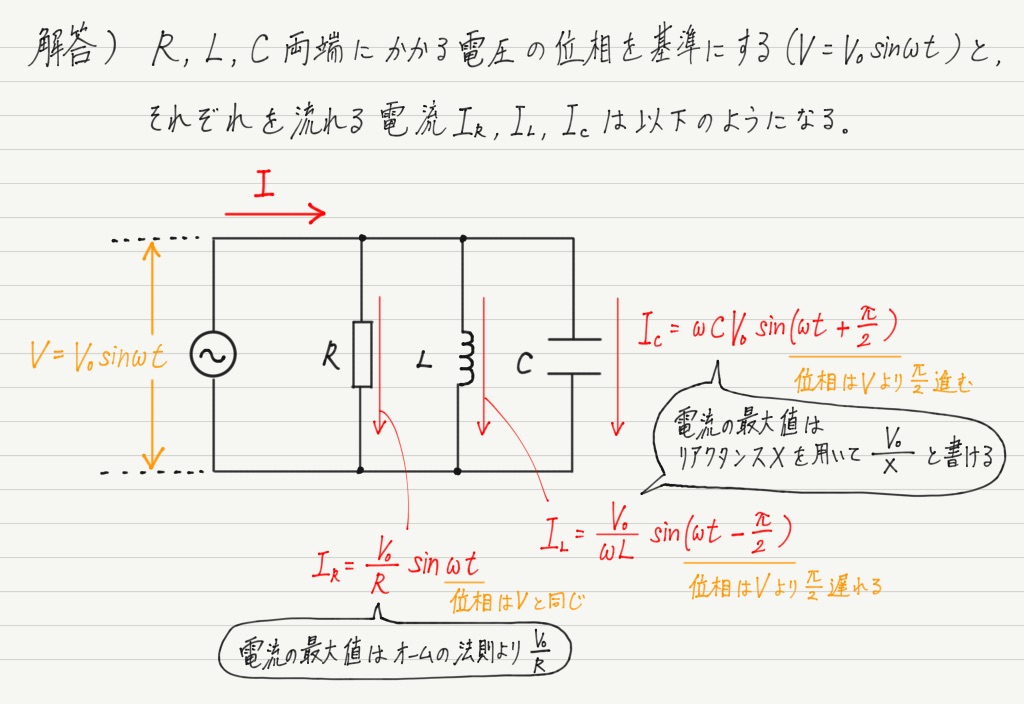
ではベクトル図に表してみましょう。
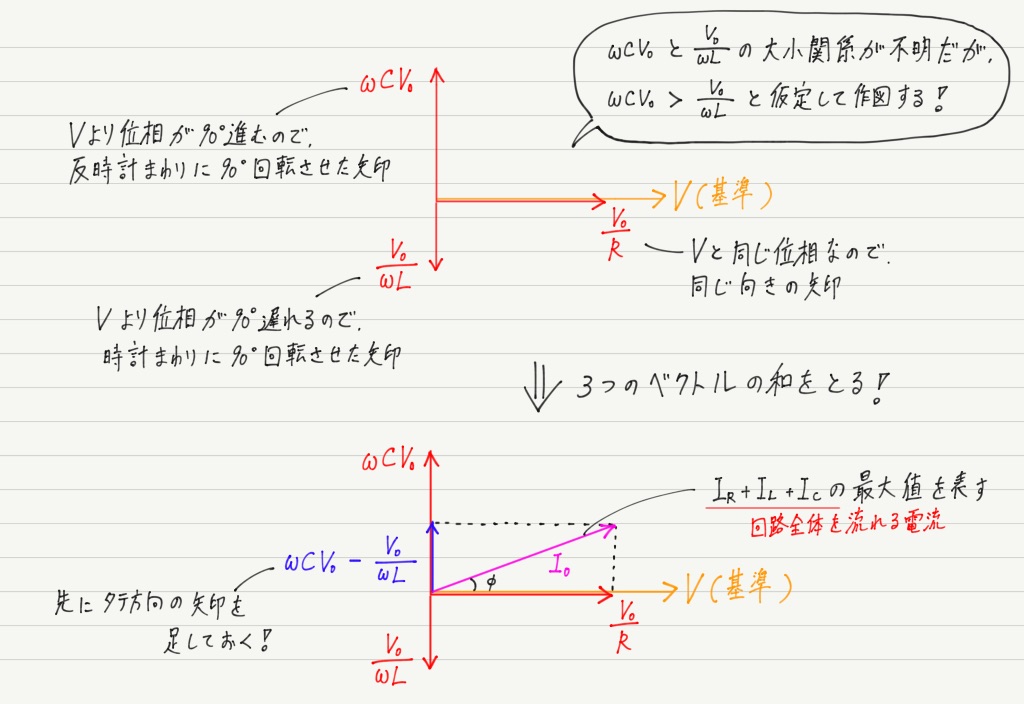
Vを基準(右向きの矢印)にして,各電流の最大値を位相に注意して書き込んでください。
回路全体を流れる電流がベクトルの和として書けたので,あとは前回同様に計算するだけ。
並列回路もベクトル図を使えばこのようにあっという間!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回はRLC回路の挙動について,もう少し掘り下げて考察していきたいと思います。