磁場の中で導線に電流を流すと,導線が力を受けることを以前学びました。
そして,その力の向きはフレミング左手の法則に従うのでした。
今回はその電流が受ける力についてもう少しだけ掘り下げてみたいと思います!
目次
力を受けているのはどれ?
以前学習したときは「電流が受ける力」と表現しましたが,導線を流れる電流の正体は自由電子なので,「磁場から力を受けているのは自由電子である」と考えるのが自然です。
実際この考えは正しく,荷電粒子が磁場の中を運動すると,磁場から力(ローレンツ力)を受けることが知られています。
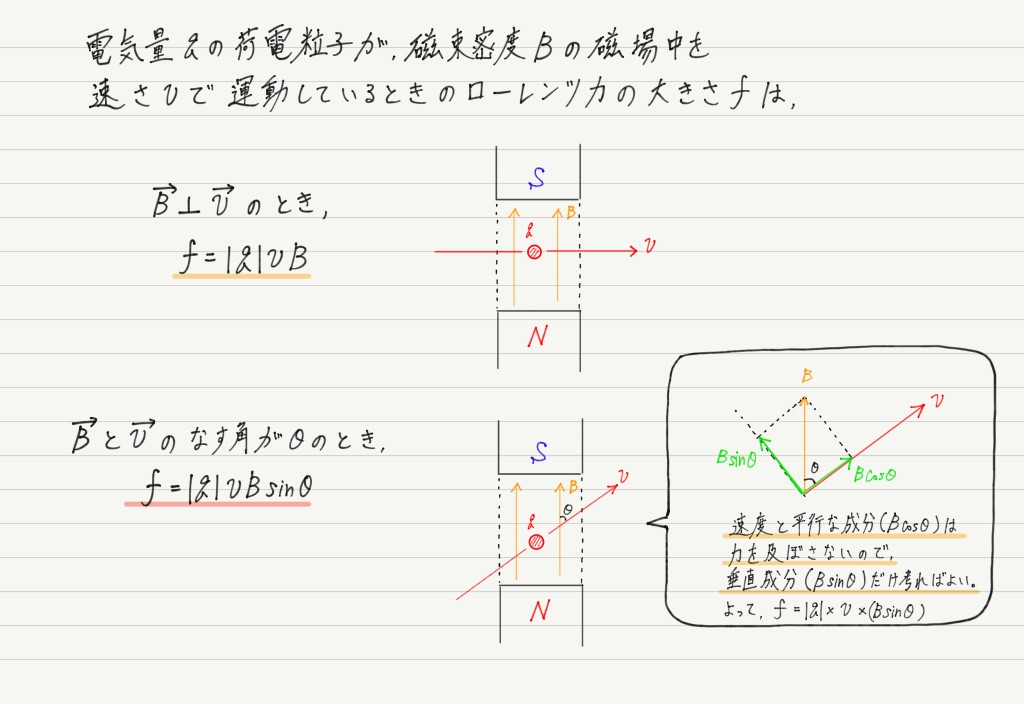
ローレンツ力の大きさは以下の式で求められるので,しっかり覚えておきましょう!
(力の“大きさ”なので,マイナスがつかないようにqに絶対値をつけておいた。)
磁場となす角がθのときにsinθを使って磁場と垂直な成分に分けるのは,電流が磁場から受ける力のときと同じですね!
ローレンツ力の向き
ローレンツ力の大きさは公式で計算するとして,向きはどうなるでしょう?
電子1つ1つが受けるローレンツ力 f を寄せ集めたものが電流が磁場から受ける力 F になるので,fとFの向きは一致するはずです!
ということは,結局フレミング左手の法則!
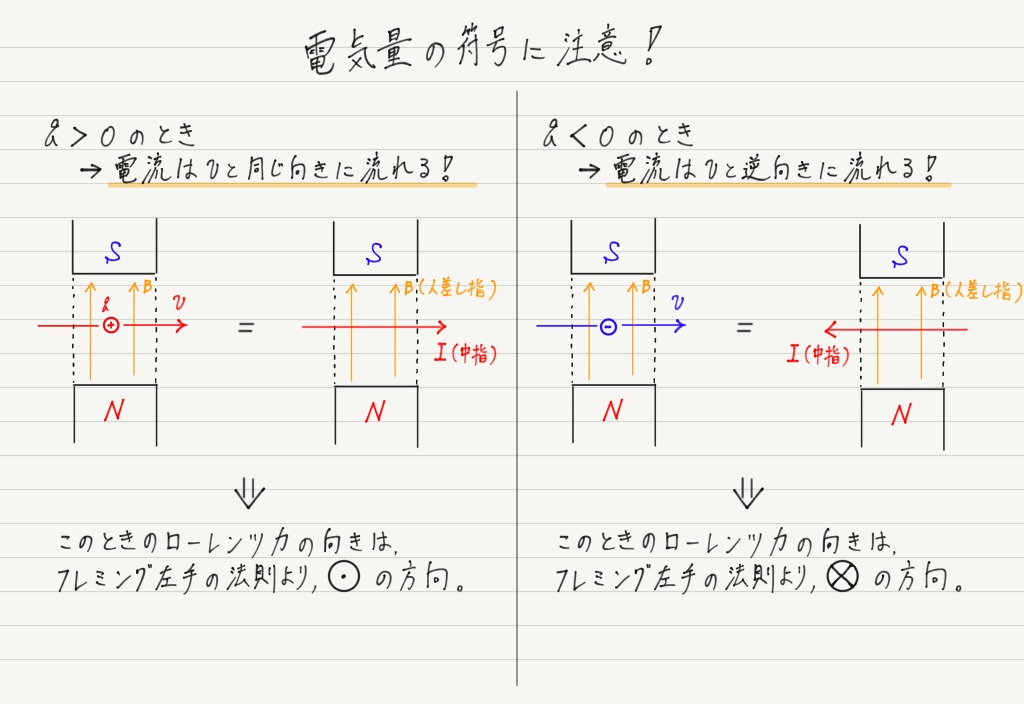
ただし,中指の向きに注意してください。
フレミング左手の法則における中指の向きは,あくまでも “電流が” 流れる向きであって,“荷電粒子が” 動く向きではありません!
荷電粒子の動く方向と電気量の符号に注意して,電流の向きを把握してからフレミング左手の法則を適用するようにしましょう。
短い記事でしたが,今回はここまで。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
はたらく力が分かれば運動が調べられる!
ということで,次回は荷電粒子の運動を調べていきましょう。