電気力線という概念は元々は「電場をイメージしやすくするために矢印を使って表す」だけのもので,それ以上でもそれ以下でもありませんでした。
数学に不慣れなファラデーが,電場を視覚的に捉えるためだけに発明したものだから当然です。
ところが,とある天才がこの電気力線に目をつけました。
「こんな便利なもの,使わない手はない!!」と。
その天才の名はガウス(※ 実際に数学的に表現したのはマクスウェル。どちらにしろ天才的な数学の才能の持ち主)。
彼は電気力線を計算に用いてある法則を発見します。 それが今回の主役の「ガウスの法則」。
天才ファラデーに唯一欠けていた数学の力を,数学の天才が補って見つけた法則なんだからもう最強。
この法則をマスターすると,イメージだけの存在だった電気力線が電場を計算する上での強力なツールに化けます!!
(※あくまでも高校物理のサイトなので,ガウスの法則の説明はしますが,証明はしません。立体角や面積分を用いる証明をお求めの方は他サイトへどうぞ。)
電気力線の追加ルール
ガウスの法則に入る前に,電気力線の本数について確認します。
電場が強いほど電気力線は密になるというのは以前説明した通りですが,そのときは電気力線のイメージに重点を置いていたので,「電気力線を何本書くか」という話題には触れてきませんでした。
実は電気力線の本数には明確な決まりがあります。
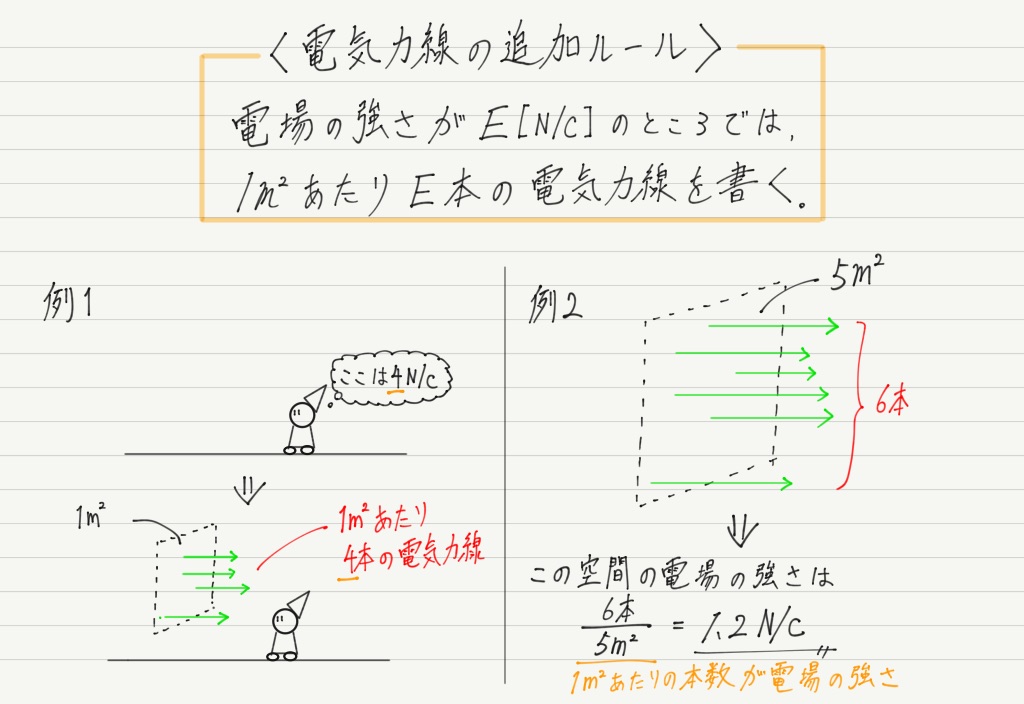
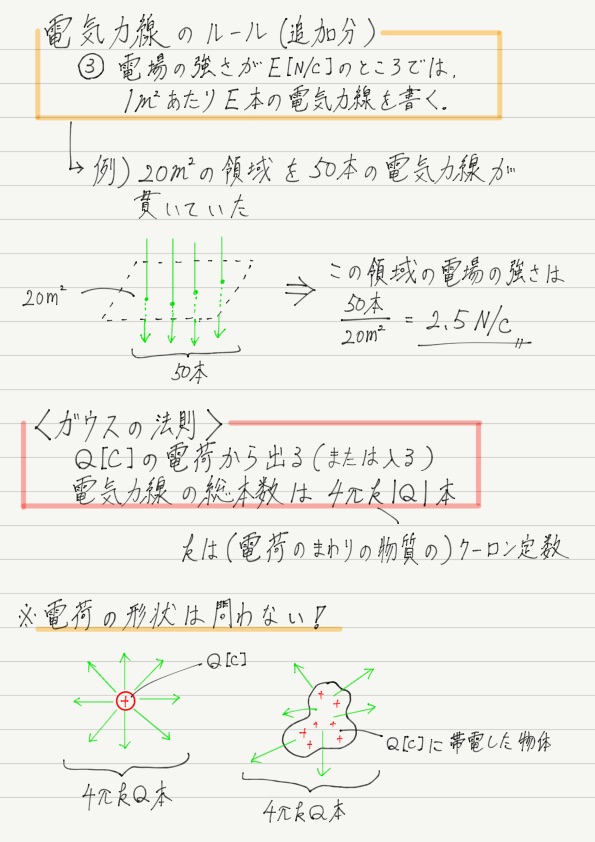
それは,「電場の強さがE[N/C]のところでは,1m2あたりE本の電気力線を書く」 というものです。
以前の記事で電気力線のルールを2つ紹介しましたが,これを3つ目のルールとしましょう。
もし電場の大きさが1000N/Cだったら,電気力線を1m2あたり1000本書かなきゃいけないのでしょうか?
安心してください。 このルールはあくまで約束事です。
ルール通りにやるなら1m2あたり1000本書くところですが,大変なので普通は省略して数本だけ書いて終わりにします。
逆に言えば,図に書いてある電気力線の本数は実際の本数とは異なるので注意が必要です。
電気量と電気力線
ここまでに分かったことをまとめましょう。
① 電荷があると電場が生じる。
② 電荷のもつ電気量が大きいほど電場は強い。
③ 電場が強いと単位面積あたり(1m2あたり)の電気力線の本数は増える。
電気量の大きさと電場の強さの間には関係(上記の②)があって,電場の強さと電気力線の本数の間にも関係(上記の③)がある…
ということは,電気量の大きさと電気力線の本数も何らかの形で関係しているのではないかと予想できます!
電気力線の総本数を求める
電気量の大きさと電気力線の本数の関係は,実はこれまでに学んできた知識から導くことが可能です!
空間に置かれたQ[C]の点電荷のまわりの電場の様子は電気力線を使って書けます(Qが正なら点電荷から出る方向,Qが負なら点電荷に入る方向)。
問題は Q[C]の点電荷から何本の電気力線が出ているかです。
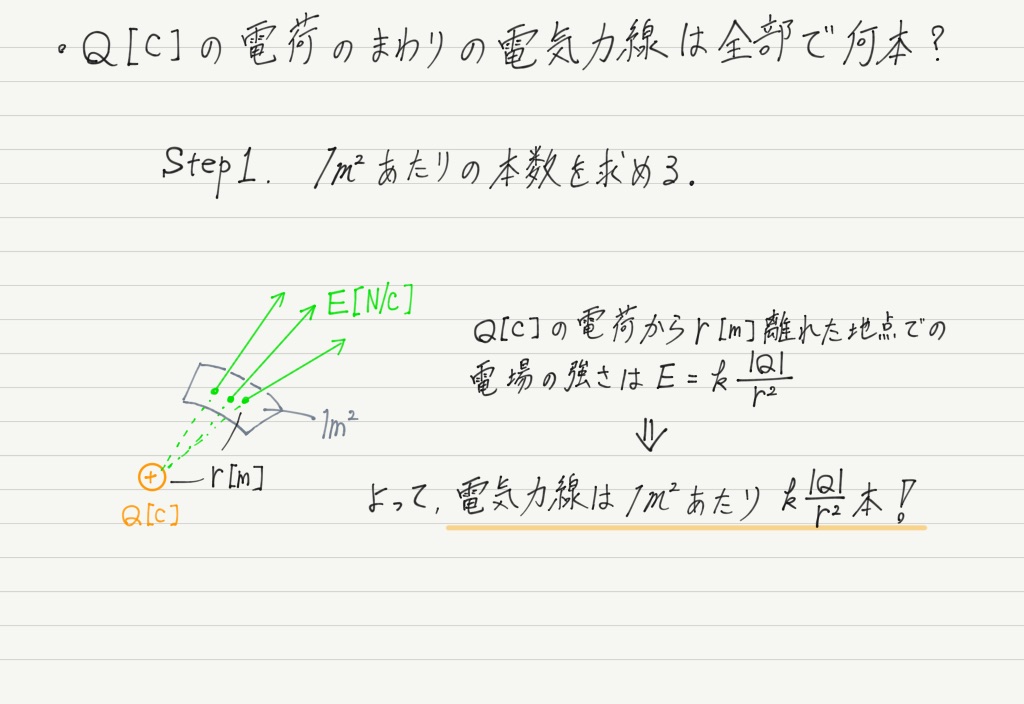
Step1として,まずは1m2あたりの本数を調べましょう。 公式を使って電場の強さを求めればOKですね!
次にStep2。
Step1では1m2という限られた面積を通る電気力線の本数しか調べませんでしたが,電気力線は点電荷を中心に全方向に伸びています。
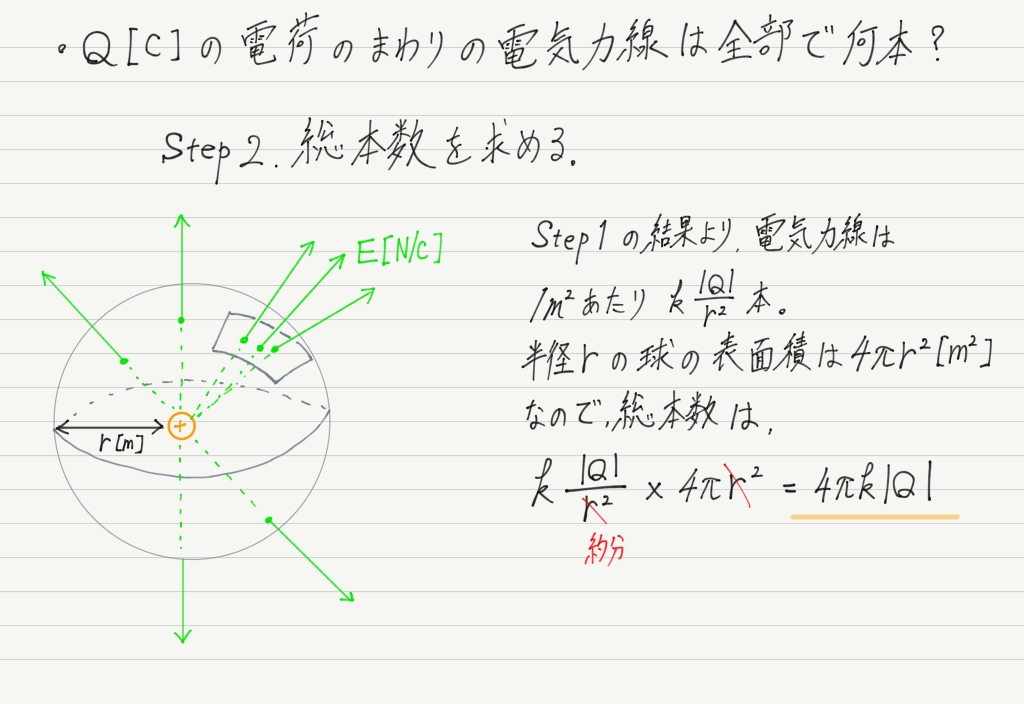
全部の本数を数えるために,点電荷を半径r[m]の球で囲みましょう(実際に囲むのではなく,見えない壁で囲む様子を想像してください)。
あとはStep1の結果を用いて計算するだけ。
Q[C]の点電荷から出る(または入る)電気力線の本数は全部で4πk|Q|本と判明しました!
ガウスの法則の真価
結論だけ述べると,ガウスの法則とは,「Q[C]の電荷から出る(または入る)電気力線の総本数は4πk|Q|本である」というものです。
上の説明では点電荷で計算しましたが,ガウスの法則の最重要ポイントは,点電荷だけに限らず,どんな形状の電荷でも成り立つことです(点電荷以外でも成り立つことを証明するには高校数学だけでは足りないので証明は略)。
上では電場の大きさから電気力線の総本数を求めましたが,逆に電気力線の総本数が分かれば,逆算することで電場の大きさを求めることができます。
その電気力線の総本数を教えてくれるのがガウスの法則なのです。
では,ガウスの法則の真価を味わうためにひとつ例題をやってみましょう。
点電荷以外でも電場が計算できるということを実感してほしいので,平面電荷(電荷が分布した金属板)がつくる電場の大きさを求めてみることにします。
ガウスの法則を適用して電場を求めるには次の手順を踏みます。
手順① 帯電体を囲む領域を設定
手順② 囲まれた領域内に何Cの電気量があるかを確認
手順③ 囲んだ領域から出ていく電気力線が貫く面の面積を求める
さっそく実践してみましょう。
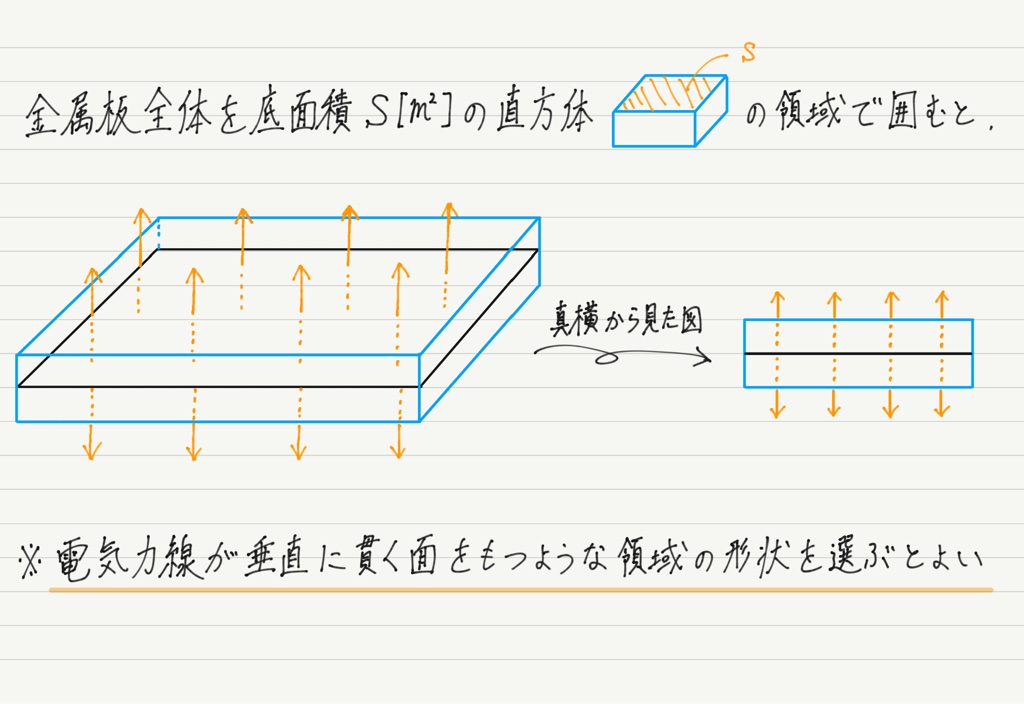
まずは手順①。 先ほど点電荷を半径rの球で囲んだように,今回の平面電荷も何かしらの領域で囲んでやります。
点電荷のときは球で囲みましたが,今回は直方体で囲みます。
電荷をどんな形状の領域で囲むのかが腕の見せ所です。 これさえできれば残りの手順は楽勝。
手順② 囲んだ直方体の中には平面電荷がまるごと入っているので,電気量は+Q
→ガウスの法則より,直方体から出ていく電気力線の総本数は4πk0Q本
手順③ 電気力線は直方体の上面と下面を貫いているが,側面は貫いていない
→電気力線が通り抜ける面積は2S
ここまで分かればもう電場は求められたも同然。 ということで解答はこちら↓
この平面電荷のつくる電場ですが,これはただの例題ではなく,次回以降の話の主役です!
この先,話は点電荷から平面電荷に移ります。
点電荷から話が急に変わって面食らう人が多いですが,ガウスの法則がこれまで学んできた点電荷と,これから学ぶ平面電荷のつなぐ架け橋になっているのです。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
これまで電気回路には電源の他には抵抗しかつなぐものがありませんでしたが,次回は電気回路に新たな部品を導入します!