いよいよ電気における最初の大事な法則である,オームの法則に入ります!
オームの法則そのものは中学校でも習っていますが,理科が得意でなかった人はおそらく使いこなせていないと思います(私もそうでした笑)。 そこで,ここでは1からオームの法則を学び直しましょう!
さて,オームの法則をどう使っていいかわからないという人でも,電圧 = 抵抗 ✕ 電流という公式ぐらいは覚えているんじゃないでしょうか?
この式の使い方や意味を説明する前に,まずはこの式に登場する,電流,電圧,抵抗の3つについて理解を深めましょう。 今回は抵抗にスポットを当てていきます。
「抵抗」とはなにか
導体のように電気を通す物質なら電流がスムーズに通るのかというと,そういうわけでもなく,必ずある程度の “通りにくさ” が存在します。 その電気の通りにくさを数値で表した量が抵抗で,単位には Ω(オーム)を使います。
…と,これだけでは寂しいので,抵抗は何によって決まるのかについてお話しましょう。
材質によって決まるんじゃないの?と思われるかもしれませんが,それは半分正解で半分ハズレ。 なぜなら,同じ材質で異なる抵抗をもつ部品をつくることができるからです。
それを理解するために,「抵抗=デコボコした道」とイメージしてください。 そして,あなたが電気となって,その道を通るところをイメージしましょう。 これ以降,この「電気が通るデコボコ道」のイメージを基に解説します。
抵抗の値はどのようにして決まるか
デコボコ道,イメージできましたか?
では,この道の “通りにくさ” は何によって決まるでしょうか? それは,
①道の長さ ②道の幅 ③道のデコボコ具合
によって決まります。 ひとつずつ見ていきましょう。 まずは①。
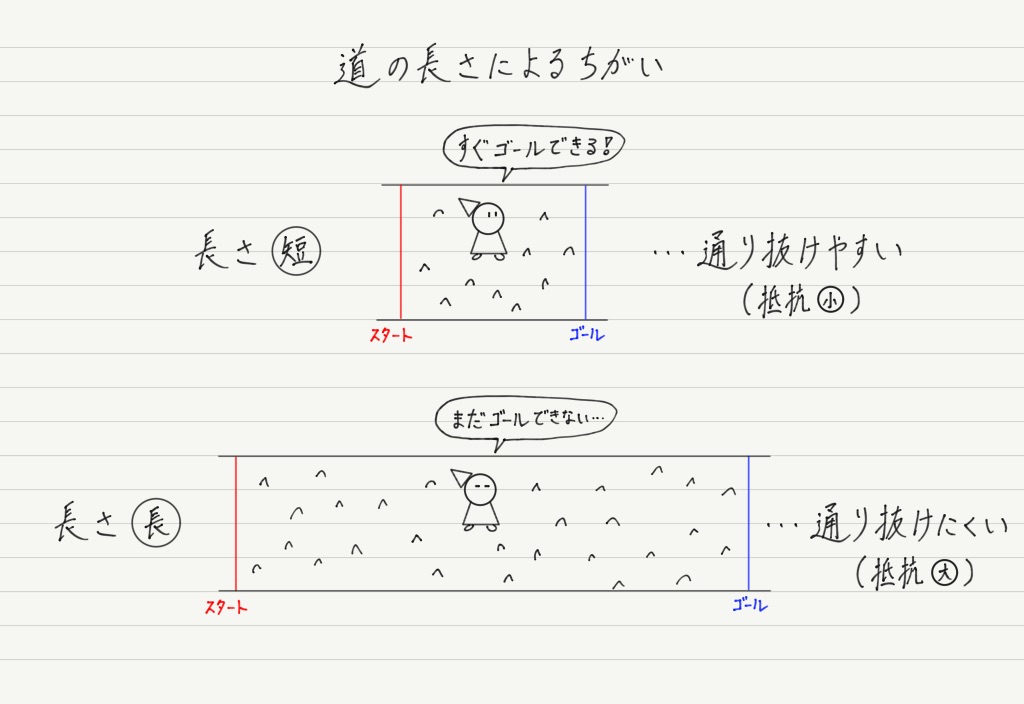
同じデコボコした道でも,長ければ長いほど通り抜けにくいというのはイメージできるかと思います。
速さが一定のとき,道の長さが2倍になれば,通り抜けるのにかかる時間も単純に2倍になります。
つまり,道の長さと抵抗は比例しています!
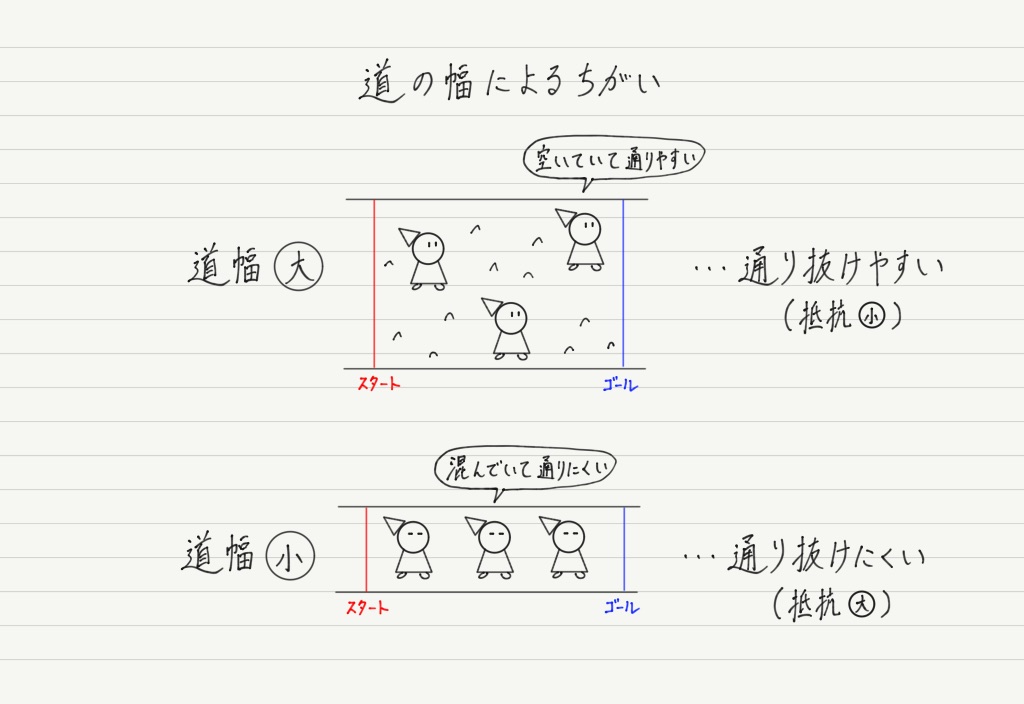
次に②ですが,これもイメージしやすいでしょう。 だって道幅は狭いより広いほうが通りやすいに決まってるじゃん!!
通る人数が1人だけなら変わらないですが,抵抗はたくさんの自由電子が通るので,狭いと渋滞しちゃうのです。
道幅が小さくなると,抵抗は逆に大きくなるので,反比例の関係にあることがわかります。
いまは道でイメージしてもらっていますが,実際の抵抗は円柱状の物体なので,道幅=円柱の断面積(底面積)になります。
最後に③。 道の長さと道幅で通りにくさが変わってくることはわかっていただけたと思います。
では,長さも幅も同じ道なら,全部同じ通りやすさなのかというと,必ずしもそうとは限りません。デコボコ具合がちがうかもしれないからです。
同じ長さと道幅で比べたときの「デコボコ具合のちがい」が「材質ごとの電気の通りにくさのちがい」を表していて,これを抵抗率と呼びます。
物質は電気の通りやすさで,導体と不導体(絶縁体)に分類されますが,これは正確には抵抗率の値で分類されるものです。
導体はどれも小さい抵抗率をもちますが,もちろん材質によって差があります。 抵抗率が小さい導体で道をつくるとあまりデコボコしていない道ができ,抵抗率が大きめの導体で道をつくるとデコボコした道ができます。
蛇足ですが,世の中にはたくさんの物質があるので,「導体ほど小さくないが,不導体ほど大きくない抵抗率をもつ物質」も存在し,半導体と呼ばれています。 半導体は導体と不導体の中間の性質をもつ,一見すると中途半端に思える物質ですが,現在のテクノロジーには欠かせない重要なものです。 興味のある方はぜひ調べてみてください!!
今回のまとめノート
たまに勘違いしている人がいるので補足しておきますが,回路に用いる抵抗は導体でできています。不導体ではありません。 不導体は電気がほぼ通れないので,それだと回路には使えませんよね(-_-)
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次は電流について理解を深めていきましょう!