今回はいよいよエネルギーを使って計算をします!
大事な内容なので気合を入れて書いたら,めちゃくちゃ長くなってしまいました…笑
時間をたっぷりとって読んでください。
力学的エネルギーとは
前回までに運動エネルギーと位置エネルギーについて学びました。
運動している物体は運動エネルギーをもち,基準から離れたところにある物体は位置エネルギーをもちます。
そうすると例えば「高いところを運動する物体」は運動エネルギーと位置エネルギーを両方もちます。
こういう場合に,運動エネルギーと位置エネルギーを一緒にして扱ってしまおう!というのが力学的エネルギーの考え方です。
「一緒にする」というのはそのまんまの意味で,
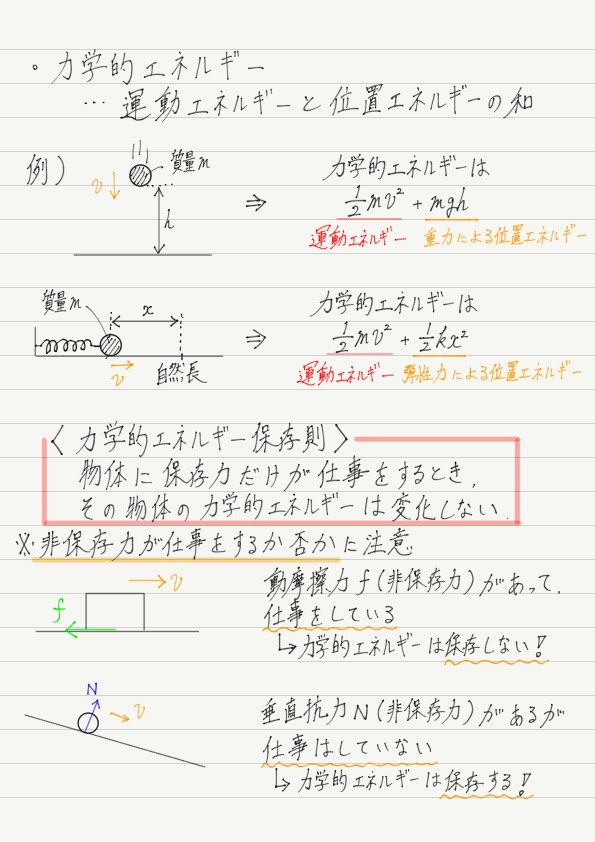
力学的エネルギー = 運動エネルギー + 位置エネルギー
です。 なんのひねりもなく,ただ足すだけ。
つまり,力学的エネルギーを求めなさいと言われたら,運動エネルギーと位置エネルギーをそれぞれ公式を使って求めて,それらを足せばOK。
力学では,運動エネルギー,位置エネルギーを単独で用いることはほぼありません。 それらを足して力学的エネルギーの形で扱うのが普通です。
【例】自由落下
力学的エネルギーを考えるメリットは何かというと,それはズバリ「力学的エネルギー保存の法則」でしょう!(以下,「力学的エネルギー保存則」と略す)
と,その前に。 力学的エネルギーは本当に保存するのでしょうか? 自由落下を例にとって説明します。
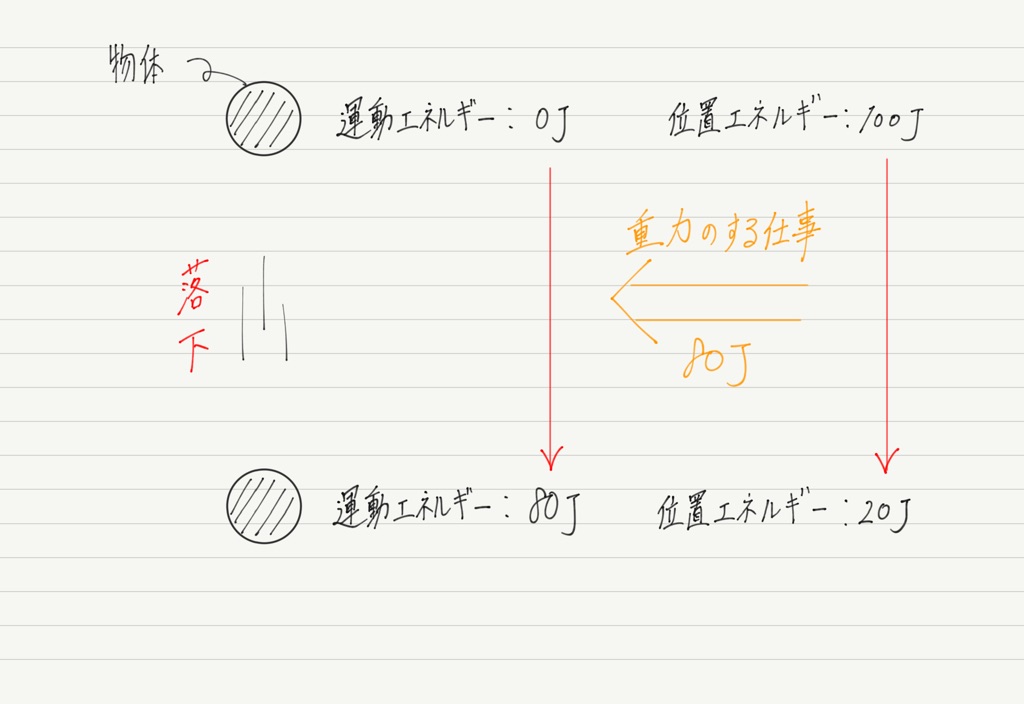
まず,位置エネルギーが100Jの地点から物体を落下させます(自由落下は初速度が0なので,運動エネルギーも0)。
物体が落下すると高さが減っていくので,そのぶん位置エネルギーも減少することになります。
ここで「エネルギー = 仕事をする能力」だったことを思い出してください。
仕事をすればエネルギーは減るし,逆に仕事をされればそのぶんエネルギーが蓄えられます。
上の図だと位置エネルギーが100Jから20Jまで減っていますが,減った80Jは仕事に使われたことになります。
その80Jの仕事をしたのは明らかに重力!
重力が,高いところにあった物体を低いところまで移動させたのです。
一方,物体は仕事をされた分だけエネルギーを蓄えます。 初速度0だったのが,落下によって速さが増えているので,運動エネルギーとして蓄えられていることになります。
つまり,重力のする仕事を介して,位置エネルギーが運動エネルギーに変化したわけです!!
いまの話を式で表すと,
ここでちょっと式をいじってみましょう。 いじるといっても,移項するだけ。
なんと! 両辺ともに「運動エネルギー + 位置エネルギー」の形になっています。
力学的エネルギー突然の登場!!
保存則という切り札
上の式をよく見ると,「落下する前の力学的エネルギー」と「落下した後の力学的エネルギー」がイコールで結ばれています。
つまり,物体が落下して,高さや速さはどんどん変化するけど,力学的エネルギーは変わらない,ということをこの式は主張しているのです。
これこそが力学的エネルギー保存則!(物理では,保存 = 変化しない,という意味)
なにか現象が起こったとき,我々は変化を気にしてしまいがちですが,この法則は,
「何が変わったか」ではなく,「何が変わらなかったか」に注目せよ!
と告げています。
変化とは表面的なもので,変わらないところにこそ本質が潜んでいる,ということでしょうか?
保存則は力学的エネルギー以外にも,今後あちこちで見かけることになります。
使う際の注意点
前置きがだいぶ長くなってしまいましたが,大事な法則なので大目に見てください。
ここで力学的エネルギー保存則をまとめておきます。
まず,この法則を使う場面について。
力学的エネルギー保存則は,「運動の中で,速さと位置が分かっている地点があるとき」に用いることができます(多くの場合,開始地点の速さと位置が与えられています)。
速さや位置が分かれば,力学的エネルギーを求められます。
そして力学的エネルギー保存則によれば,運動している間,力学的エネルギーは変化しないので,これを利用すれば別の地点での速さや位置が得られます。
あとで実際に例題を使って計算してみましょう!
例題の前に注意点をひとつ。保存則と言われると,どうしても「保存する」という結論ばかりに目が行ってしまいますが,
なんでもかんでも力学的エネルギーが保存すると思ったら大間違い!!
物理法則は多くの場合,「◯◯のとき,☓☓が成り立つ」のように,「条件 → 結論」という形をしています。 結論も大事ですが,条件を見落としてはいけません。
今回も「物体に保存力だけが仕事をするとき〜」という条件がついていますね? これが超大事です!
非保存力が物体に仕事をする場合,力学的エネルギーは残念ながら保存しません。
保存力,非保存力という名前はここから来ています。
(※ 物体に非保存力がはたらいていても,仕事をしていなければ保存することに注意)
摩擦があったり,誰かが物体を手で押したりしたらアウト。 問題を解く場合はこの点によく注意してください。
例題
実際に問題を解いて,保存則の使い方をマスターしましょう。
自由落下の問題です。 この問題は等加速度運動の公式③でも解けますが,自由落下する直前の速さ(もちろん0m/s)と地面からの高さが分かっているので,今回は力学的エネルギー保存則で解いてみましょう。
力学的エネルギー保存則を使う際は,まず速さと位置が分かっている箇所と求めたい値がある箇所のそれぞれで力学的エネルギーを計算します。
今回の場合,速さと位置が分かっている箇所は落下前,求めたい箇所は地面直前。
エネルギーを求めるとき,慣れないうちは表を使うといいでしょう。
まず,求めたい値は文字でおいておきます。 それから以前やった公式を用いて,位置エネルギーや運動エネルギーを求めて表を埋めていきます。
今回のようにエネルギーが0になる部分があると,計算は比較的簡単です。
あとは力学的エネルギーどうしをイコールで結んでvを求めるだけですが,力学的エネルギー保存則が使える条件,「非保存力が仕事をしていないかどうか」は必ず確認してください。
今回の問題では,仕事をしている力は重力だけなので問題ナシ!
運動エネルギーや位置エネルギー,保存力などで不安な部分がある人は今のうちに復習しましょう。
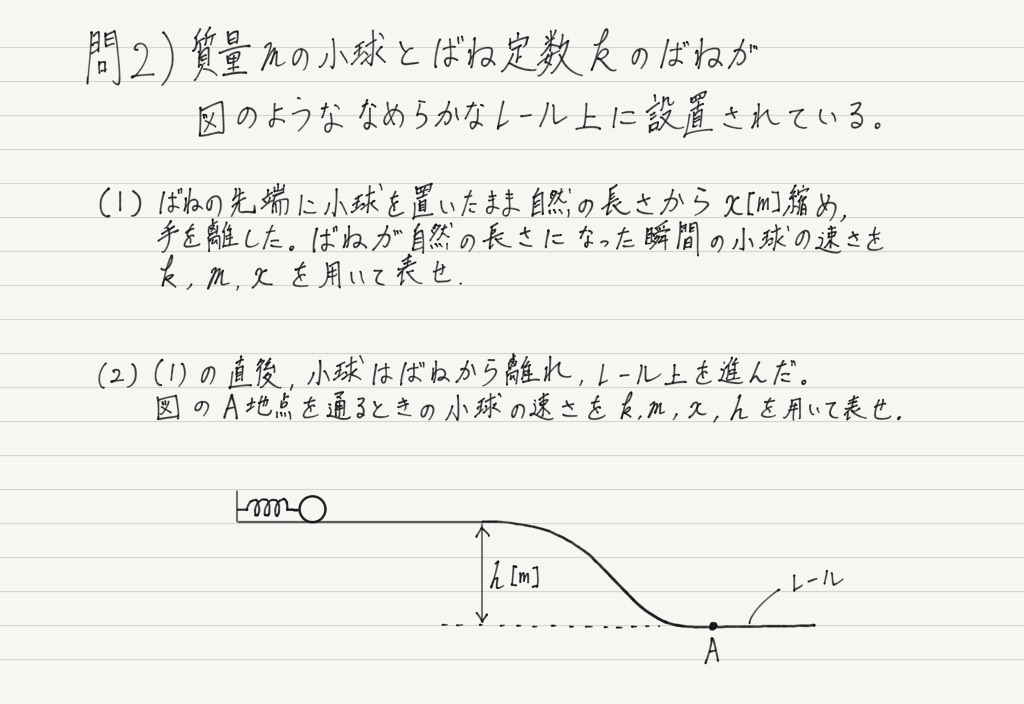
次は弾性力による位置エネルギーが含まれる問題です。
まず非保存力が仕事をしていないかチェックします。 小球にはたらく力は弾性力,重力,レールからの垂直抗力です(問題文にレールはなめらかと書いてあるので摩擦はありません)。
弾性力と重力は保存力なのでOK,垂直抗力は非保存力ですが仕事をしないのでOK。
よって,この問も力学的エネルギー保存則が使えます!
この問題のポイントはばねです。 ばねが登場する場合は,弾性力による位置エネルギーも考慮して力学的エネルギーを求めなければなりませんが,ばねだからといって特別なことは何もありません。
どんな位置エネルギーでも,運動エネルギーと足せば力学的エネルギーになります。
まずエネルギーの表を作ってみましょう!
問題の中で位置エネルギーの基準は指定されていないので,自分で決める必要があります。
ばねがあるために表の列がひとつ増えていますが,それ以外はさっきと同じ。
ここまで書ければあとは力学的エネルギーを比べるだけ!
これが力学的エネルギー保存則を用いた問題の解き方です。
まずやるべきことはエネルギーの公式をちゃんと覚えて,エネルギーの表を自力で埋められるようにすること。 そうすれば絶対に解けるはずです!
最後におまけの問題。
問2の解答では重力による位置エネルギーの基準を「小球が最初にある位置」にしていますが,基準を別の場所に取り替えたらどうなるのでしょうか?
Aの地点を基準にして問2を解き直てみてください。
では,解答を見てみましょう。
このように,基準を取り替えても最終的に得られる答えは変わりません。
この事実があるからこそ,位置エネルギーの基準は自分で自由に決めてよいのです。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
今回注意点として「非保存力が仕事をするときは力学的エネルギーが保存しない」ことを挙げました。
保存しなかったら当然保存則で問題を解くことはできません。
そのような場合,他に解決策はあるのでしょうか?