いよいよ運動の3法則もひとつを残すのみになりました。 第1法則も第3法則も,中学校で習っていることなので,高校物理における主役は今回学ぶ第2法則といっていいでしょう!
運動の第2法則は別名「運動の法則」とも呼ばれますが,そのまま「第2法則」と呼ばれることも多いです。 今回は長めの記事&大事な内容なので,時間をとって読んでください。
まずはおさらい。 運動の第1法則(慣性の法則)は,物体にはたらく力がつりあっているときに成り立つ法則でした。 しかし,いつも力がつりあっているとは限りません。
力がつりあっていないとき,物体はどうなるのか? それを示してくれるのが運動の第2法則になります。
運動の法則を読み解く
さっそくですが,運動の法則を紹介します!!
「物体に力がはたらくと,物体はその力の向きに加速度を生じる。加速度の大きさは力の大きさに比例し,物体の質量に反比例する。」
まず前半に登場する「力」というのは,合力を表しています。 たとえば物体を右向きに5.0N,左向きに2.0Nで引っ張っていたら,合力は右向きに3.0Nとなるので,右向きに加速度を生じる,ということです。
この法則の重要な点はいくつかありますが,最大のポイントは加速度です!!
力がつりあっていないとき,物体はどうなるかを示すのが運動の第2法則である,と言いましたが,力がつりあっていなければ物体は当然動き出します。 これは別に物理を勉強していなくても誰もが知っていることです。
ところが!!
「力を加えれば止まっている物体は動き出す」ところまではいいんですが,多くの人がその続きを勘違いしています!
「加える力を大きくすれば物体は速く動くので,速度は力に比例する!」
これは大間違いです!
力と速度は比例しない
なぜ間違いなのか考えてみましょう。
もし,力の大きさと速度が比例するならば,力を2倍にしたら速度も2倍,力を3倍にしたら速度も3倍,… … …となるはずです。
同じ要領で考えれば,力を0にしたら速度も0,ということになりますが…
ここで自転車を思い浮かべてください。 力強くペダルを踏めば自転車はその分速く進むので,一見すると比例関係は正しいように思えます。
しかし,ペダルを漕ぐのをやめた(=加える力が0)とき,速度は0になりますか?
なりませんよね!!
漕ぐのをやめた瞬間,ピタッと止まる自転車なんて存在しません!
漕ぐのをやめても,自転車は同じスピードで進むはずです(実際は摩擦や空気抵抗でだんだん遅くなりますが今回はこれらの影響は無視する)。
さて,慣性の法則によると,「力がはたらかないとき,動いている物体は等速直線運動をする」のでした。 力と速さが比例すると考えると,慣性の法則と矛盾してしまいます。
ではどう考えたらいいのでしょうか。 実は答えは慣性の法則に隠されています!
慣性の法則によれば,「力がはたらかなければ,物体の運動状態は変わらない」ということですが,これは言い換えると「力がはたらけば,運動状態が変わる」となります。
運動状態が変わるとは,止まっている物体は動き出し,動いている物体はその速さが速くなったり,遅くなったりする,ということです。
これってまさに加速度の話では!?
ニュートンは,力と速さが関係しているのではなく,力と加速度が関係しているということを発見したのです!!
まとめると,「大きい力を加えれば物体は速く動くようになる」は正しいけれど,力が直接速さと比例するのではなく,「大きい力ほど大きい加速度を生じるので,その結果,物体は速くなる」というのが正しい解釈になります。
質量が大きい物体は止まりにくい
運動の法則を用いて,自転車の例を正しく説明してみましょう。
ペダルを漕ぐ→正の加速度を生じる→速くなる
漕ぐのをやめる→力がはたらかないので加速度なし→等速直線運動
ブレーキをかける→負の加速度を生じる→減速する
となります。
法則の後半部分,「加速度は質量に反比例する」も大切です。
これは,質量が大きいと,同じ大きさの力でも生じる加速度が小さくなる,ということを言っています。 つまり,
質量が大きい→加速しにくく,減速しにくい
質量が小さい→加速しやすく,減速しやすい
ということ。
これを日常生活に当てはめると,たとえば自転車や車を運転するときなどは,荷物や同乗者が多いほど,減速しにくい(=止まるのに時間がかかる)ということになるので,安全運転のため頭に入れておいて損はないでしょう。
運動の法則を式で表してみる
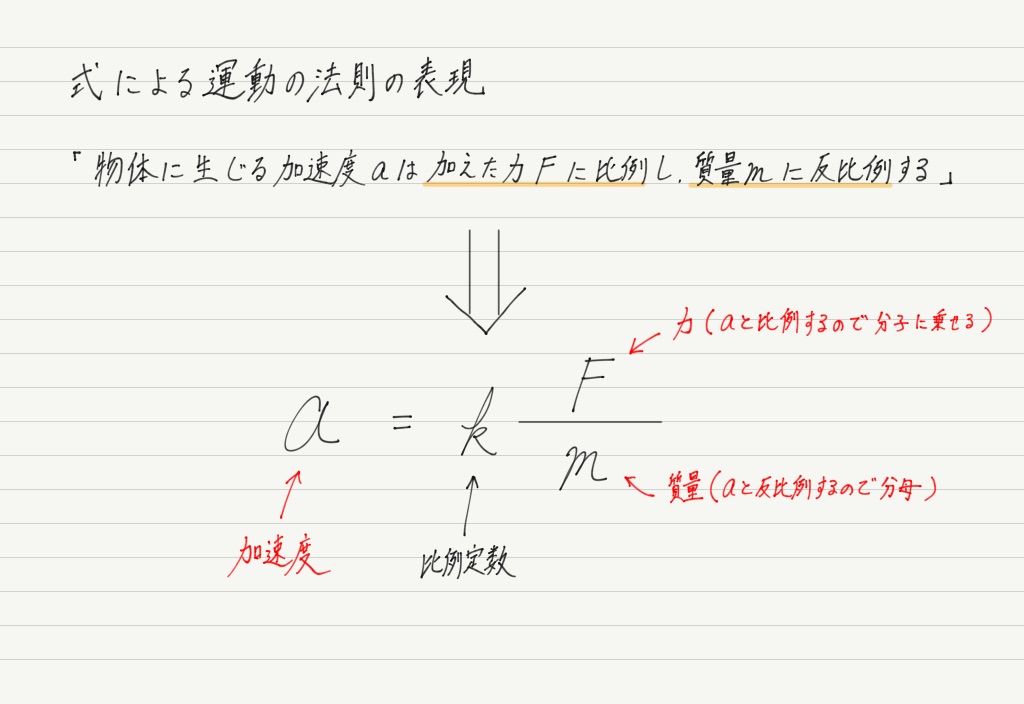
運動の法則は,加速度と力の比例関係,加速度と質量の反比例関係を述べている法則なので,式に表すことができます!!
この式はそのままでは使いませんので,覚えなくて結構です。
比例と反比例だから式として書ける!という点だけ確認しておいてください。
1Nってどれぐらいの力?
さて,ここでようやく力の単位「N(ニュートン)」が定義できます。
重力のところで,「中学校では,100gの物体にはたらく重力の大きさがおよそ1Nと習うが,それは “およそ” 1Nで,正確な1Nではない」という話をしたのを覚えているでしょうか??
そのときは「じゃあ正確な1Nって何?」という話にはあえて触れませんでしたが,運動の第2法則を習ったいま,ようやく説明できます!!
ちょっとわかりにくい気もしますが(笑),これが正しい1Nの定義になります。
せっかく1Nも決まったことだし,運動の法則の比例定数kは今後もずっと1のままにしておきましょう!
長くなってしまったので,ここまでの内容をまとめて今回は終わりにします。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
運動の法則はまだまだ奥が深いので,次回もこの続きです!