回路に複数の抵抗がつながれているとき,「合成抵抗」という考えを用いると問題が簡単に解ける(かもしれない)
…というのを以前学習しましたが,実はコンデンサーにも同じ概念があります。
今回の補講では合成抵抗のコンデンサーバージョン,「合成容量」について学んでいきましょう!
合成容量という考え方
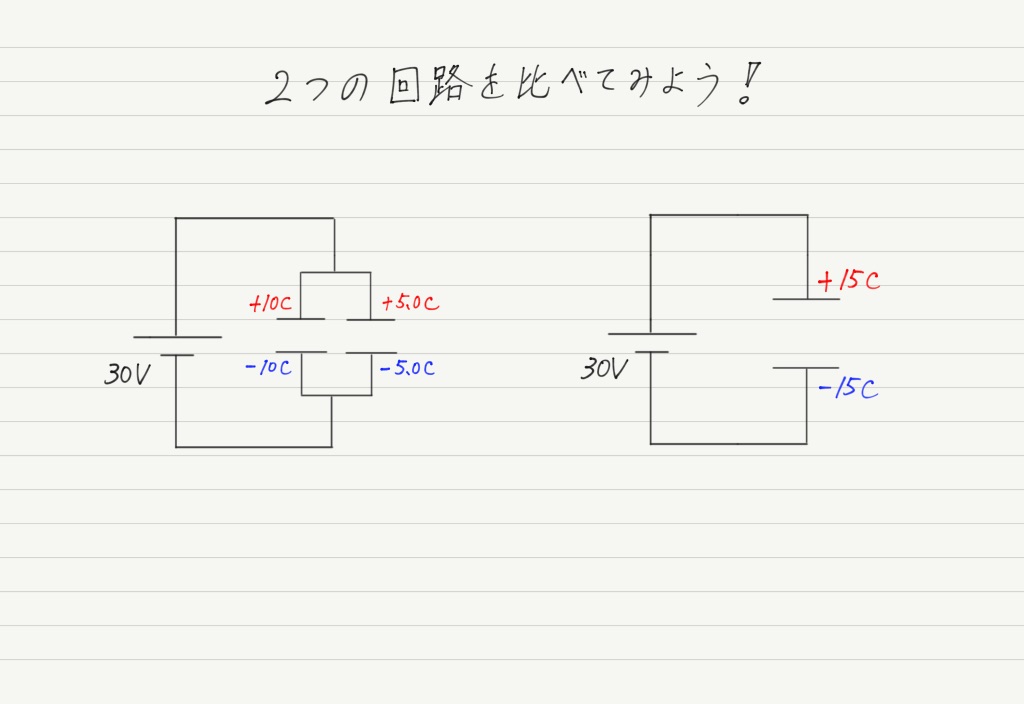
まず,この図を見てください。
回路としては別物ですが,「30Vの電源を接続したら,合計15Cの電気量が蓄えられた」という点では一致しています。
「同じ電圧をかけたら同じ電気量が蓄えられた」ということは,左の回路の2つのコンデンサーと右の回路のコンデンサーは同じ電気容量をもっているといえます!
このように複数のコンデンサーをまとめて,同じ電気容量(合成容量という)をもつ1つのコンデンサーに置き換えて考えると,問題の見通しも良くなります。
問題は何Fのコンデンサーに置き換えればいいのか?というところですが,それはもとのコンデンサーの電気容量から求めることができます。
さっそくその求め方を紹介しましょう!
並列に接続されたコンデンサーの合成
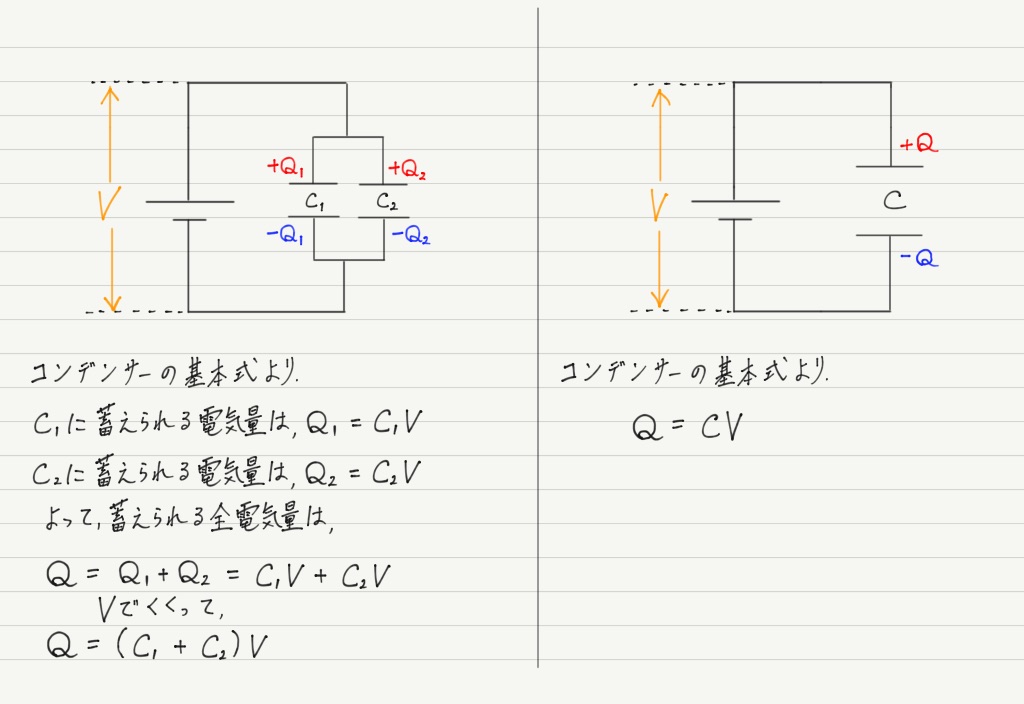
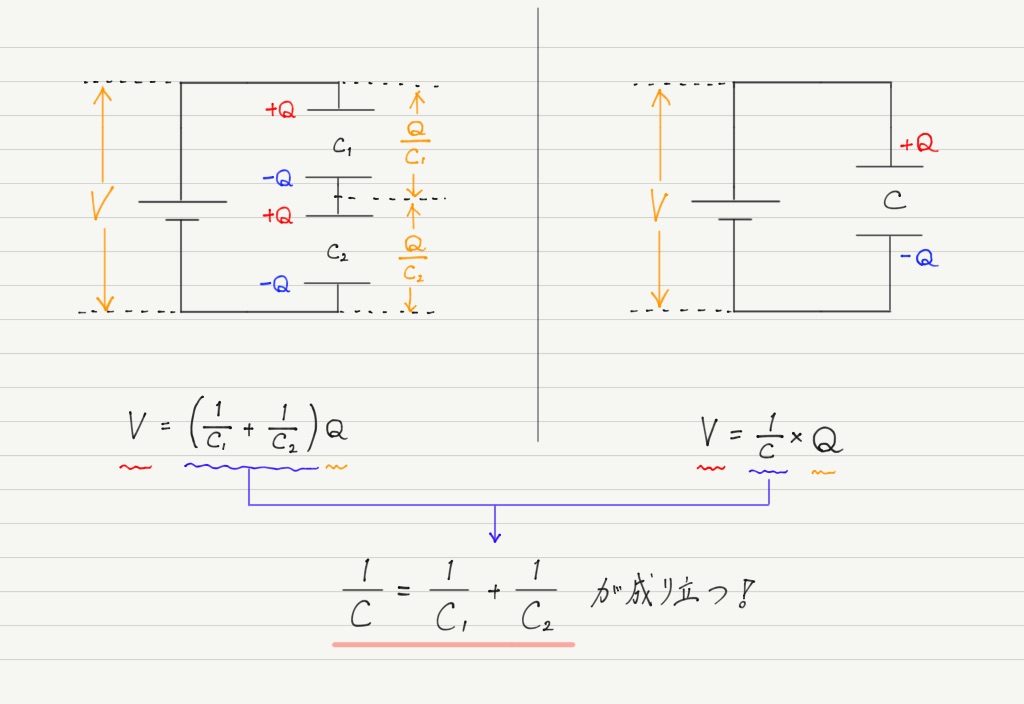
まず先ほどと同じように,コンデンサーが2つある回路と,それを1つのコンデンサーで置き換えた回路の2つを用意して比べてみましょう。
それぞれでコンデンサーの基本式を用いて計算してみます。
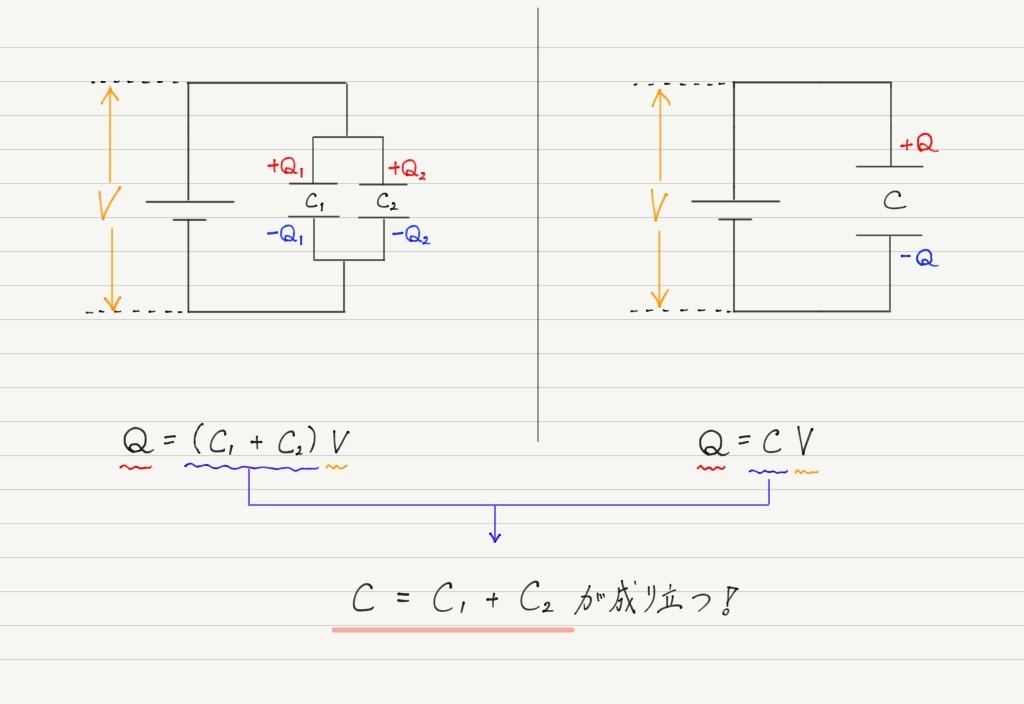
同じ電圧をかけて,同じ電気量が蓄えられたのだから,この2つの電気容量は同じにならなければいけません。 得られた式を比較してみると…
これが合成容量Cを求める式です!
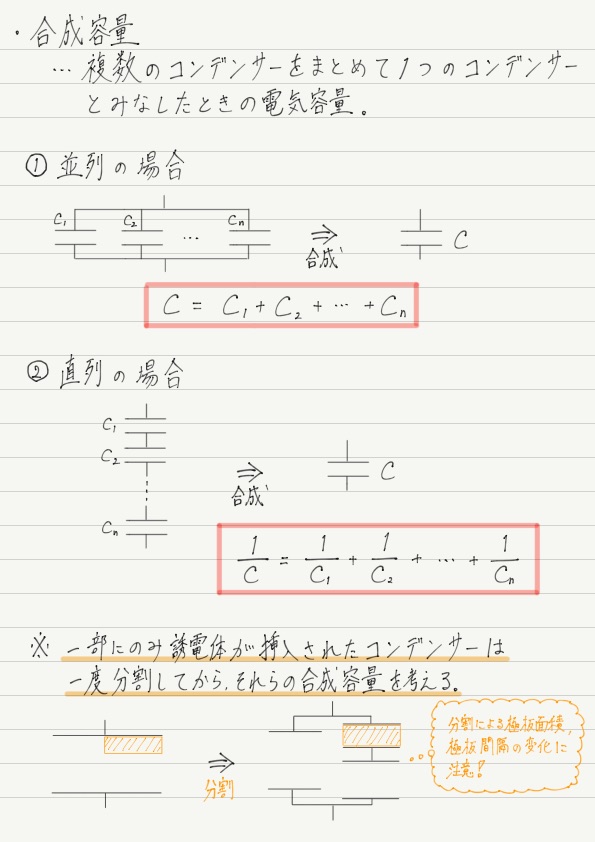
コンデンサーが並列につながれている場合は,このようにそれぞれの電気容量の値をただ足すだけで合成容量の値が得られます。
コンデンサーが3つ以上の場合も同様です。
直列に接続された抵抗の合成
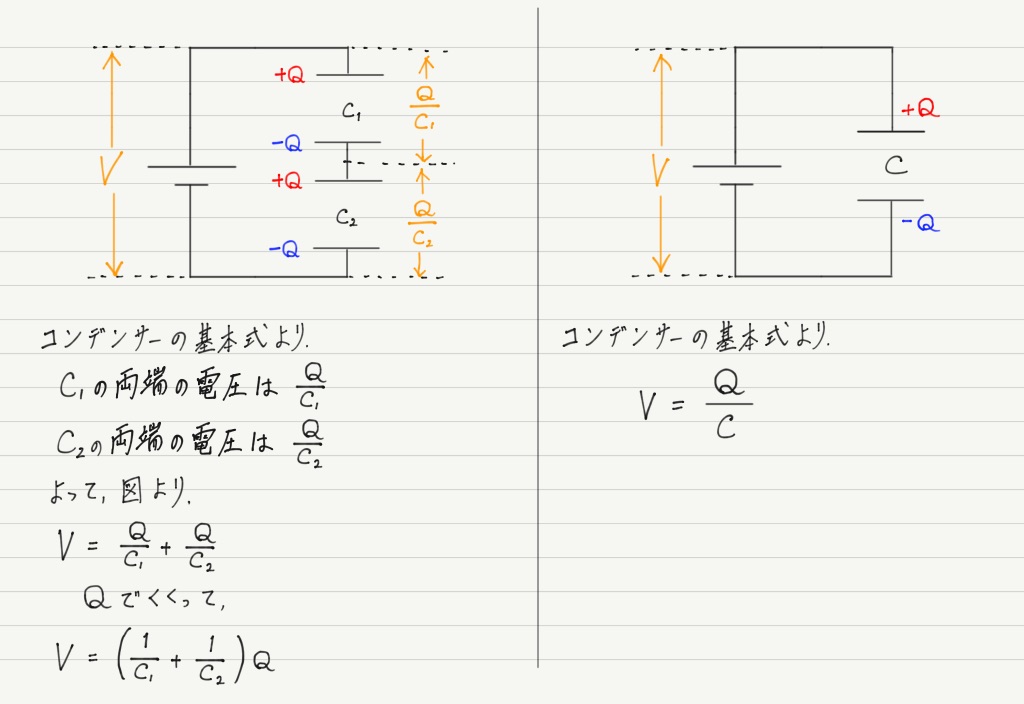
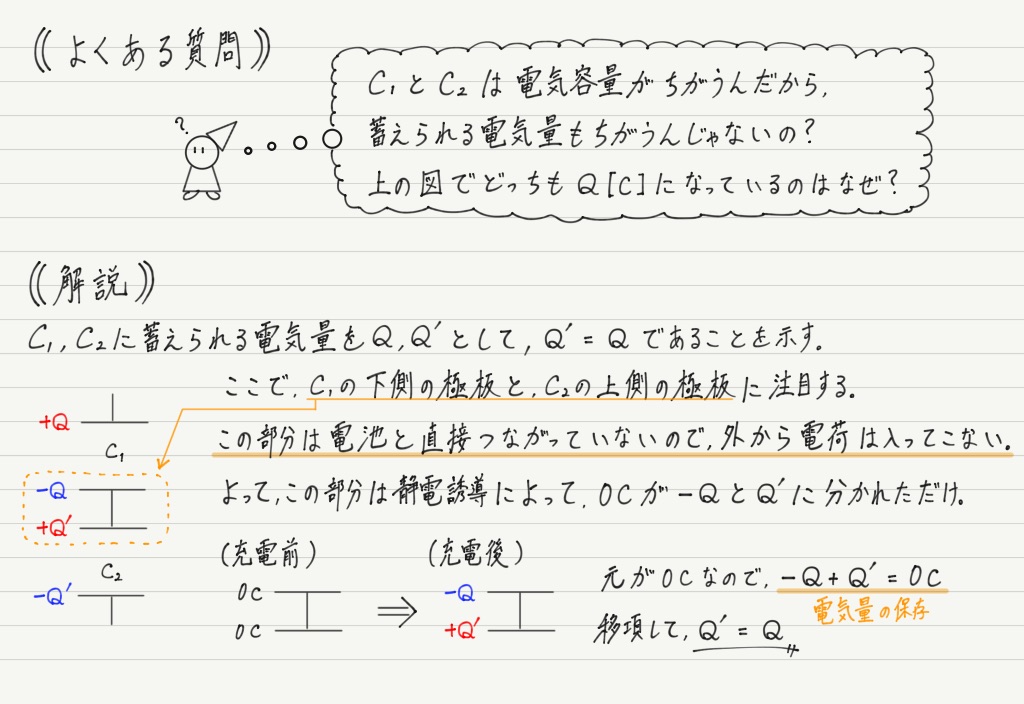
並列のときと同様に,それぞれでコンデンサーの基本式を用いて計算してみましょう。
(電池をつなぐ前,コンデンサーは充電されていないとする。)
あとはさっきと同様に式を比較するだけですが,そのまえに重要なポイントがあるので解説を挟んでおきます。
電池とつながっていない部分に関する電気量の保存は大事なのでしっかり押さえておくこと!
話を戻して,得られた式を比較。
これが直列の合成容量です!
コンデンサーが直列につながれている場合は,それぞれの電気容量の逆数をとって足したものが合成容量の逆数になります。 コンデンサーが3つ以上の場合も逆数をとって足せばOK!
…もう気づかれたと思いますが,合成容量の式は合成抵抗の式ととてもよく似ています。
ただし直列の場合の求め方と並列の場合の求め方が,合成抵抗と合成容量で逆になっていることだけはくれぐれも注意してください!
中途半端に挿入された誘電体
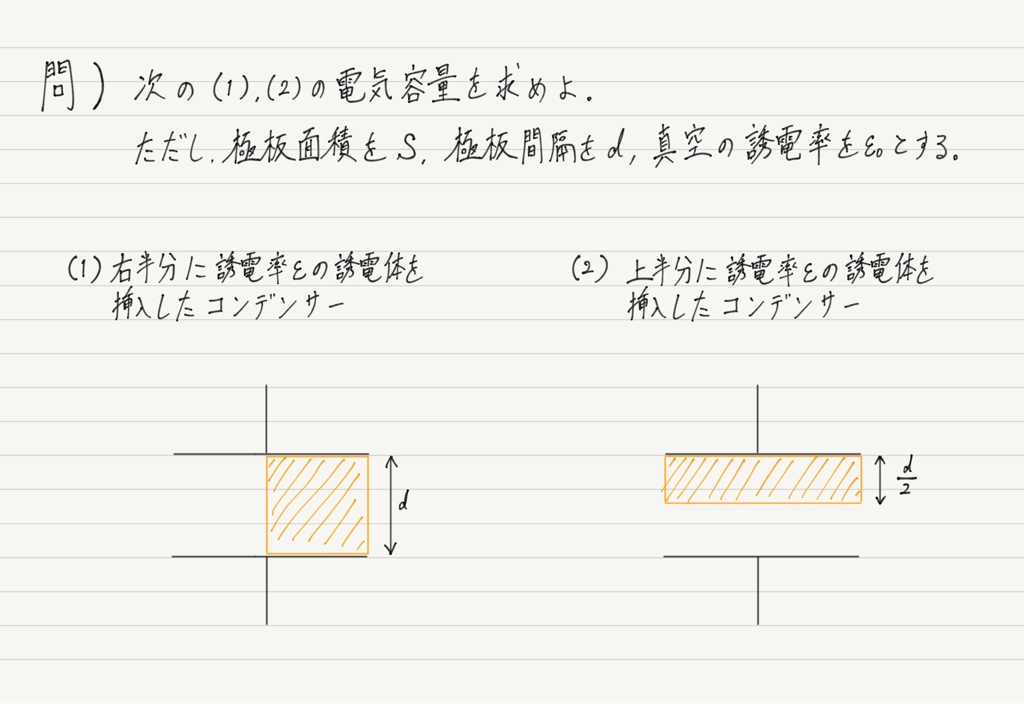
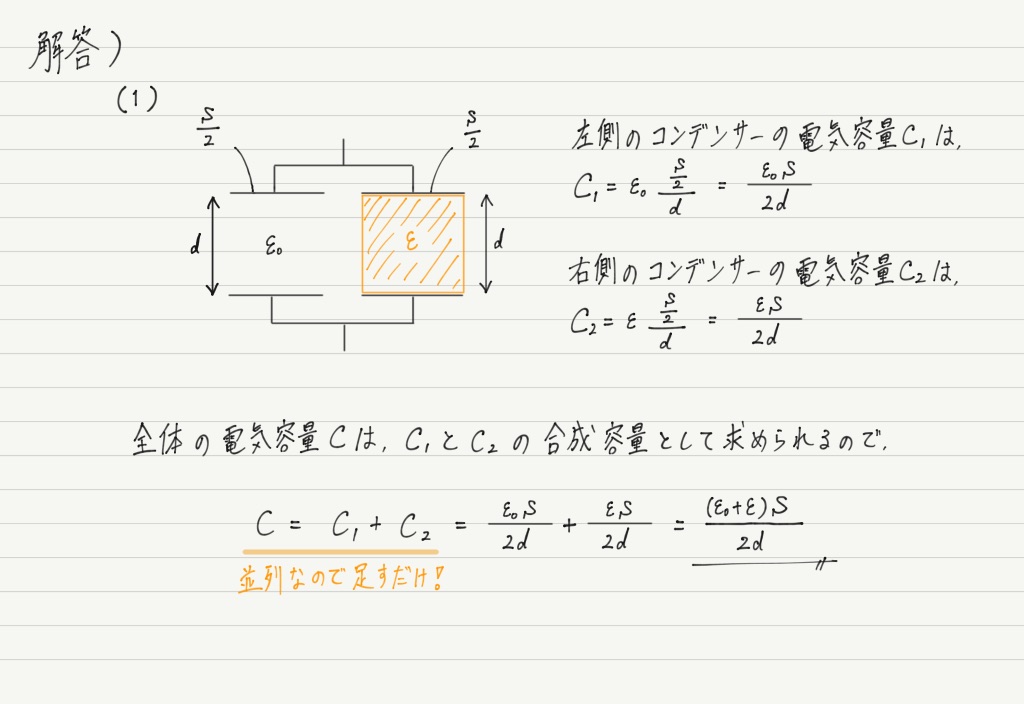
問題集などで次のような問題を見かけたことはありませんか?
実は合成容量の考え方が最も威力を発揮するのはこういうシチュエーション。
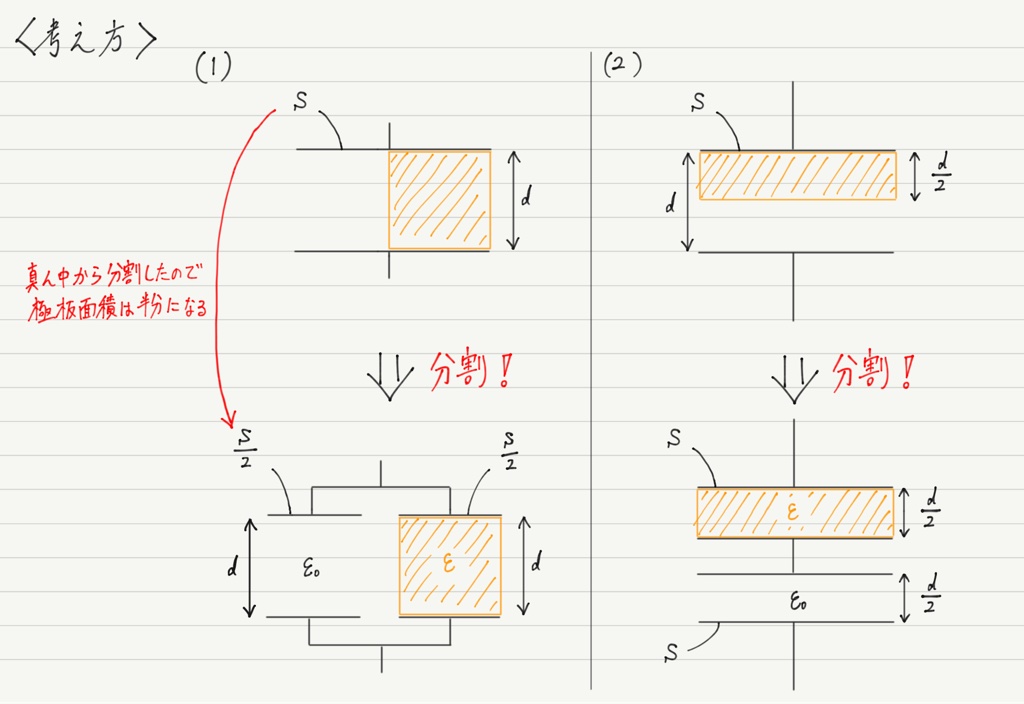
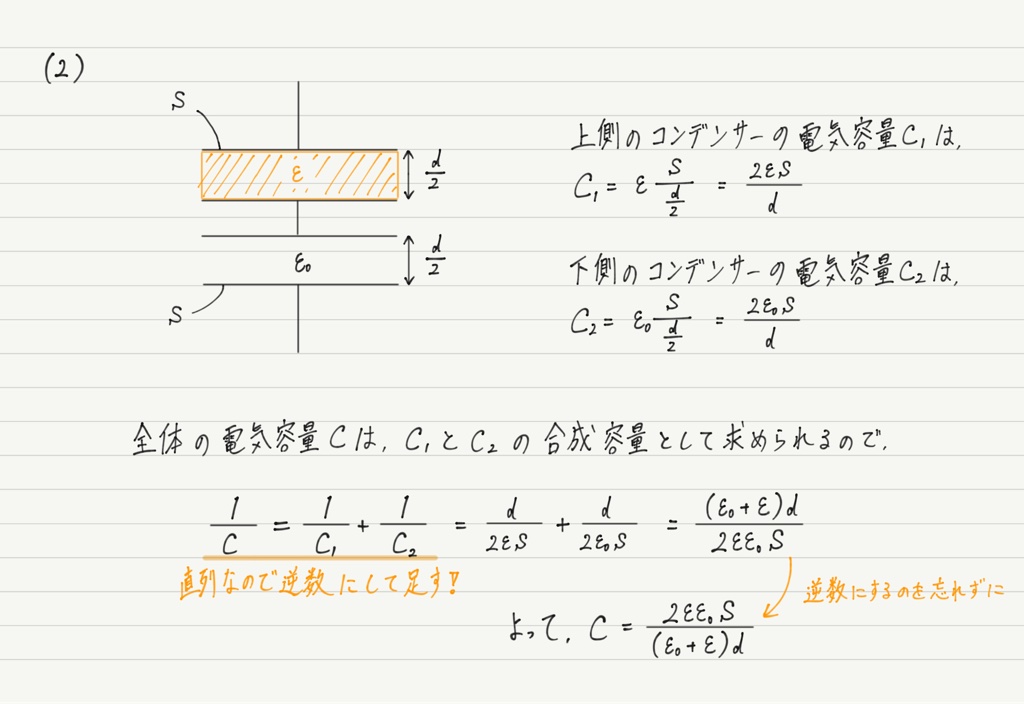
誘電体がコンデンサー全体ではなく一部にのみ挿入されている場合,コンデンサーをわざと分割して考えます!
このように分割してから各コンデンサーの電気容量を求め,そのあとで合成容量を求めればOK。
誘電体が中途半端に挿入されたコンデンサーの問題は,合成容量なくしては解けません!
別になくても困らない “おまけ” みたいな存在だった合成抵抗とは対照的です。
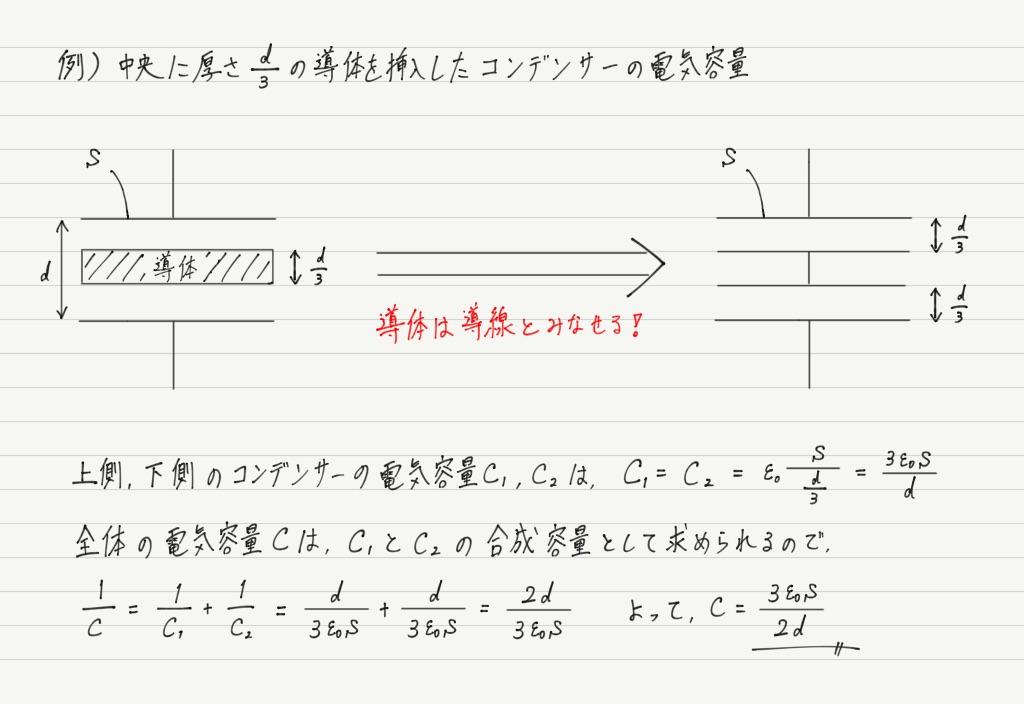
ちなみに,誘電体ではなく導体を挿入した場合は,そのぶんコンデンサーが狭くなったと考えましょう。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。