仕事（三角比編）-高校物理をあきらめる前に

物体に力を加えて移動させるとき，仕事という概念が大事になってきますが，その計算方法は以前本編で説明しました。

しかし，そのとき扱ったのは，
・力の向きと移動方向が同じとき
・力の向きが移動方向と垂直のとき
・力の向きと移動方向が逆向きのとき
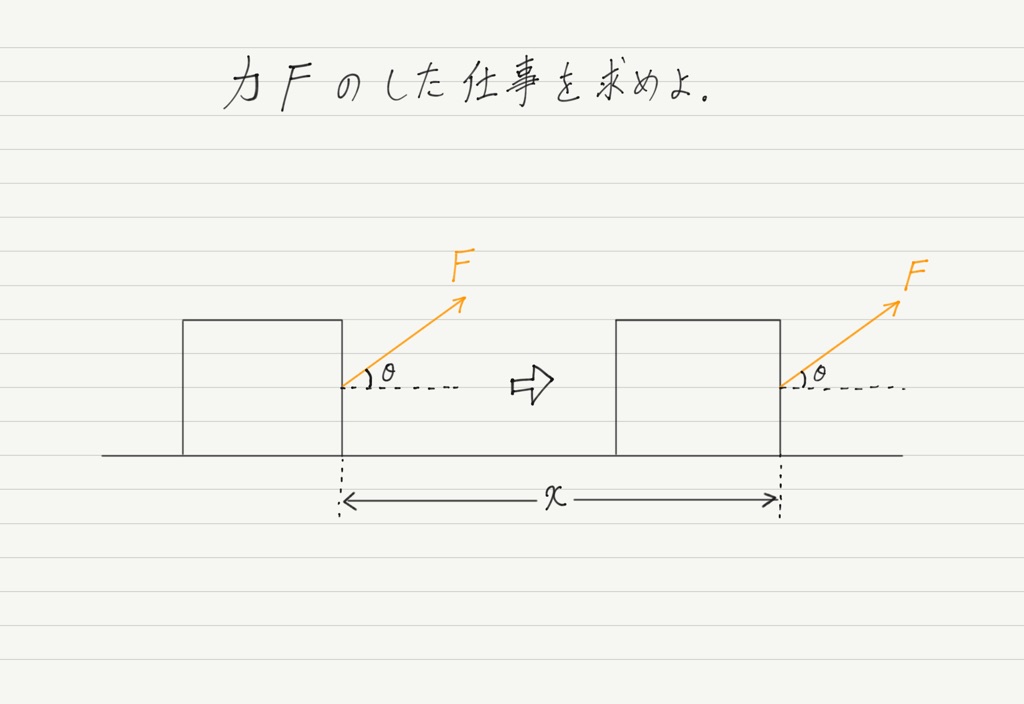
の3パターンだけです。では，次のような場合はどうすればいいのでしょう？

移動方向に対して，力が斜めを向いている！？

こんな状況あるのか？と文句を言う人もいるので一応答えておくと，スーツケースを引いて歩けばこれと同じ状況になります。

（スーツケースは斜め上に引かれているが，移動方向は水平）

今回紹介する式を使えば，このような斜め方向の力がする仕事もバッチリ計算できちゃいます！

Contents

斜めの力はとにかく分解

移動方向に対して斜め方向の力が登場したら，移動方向と垂直方向に即分解！！
物理をやる上でこれはもう常識です。

少し前に，三角比を使った分解を説明しました。

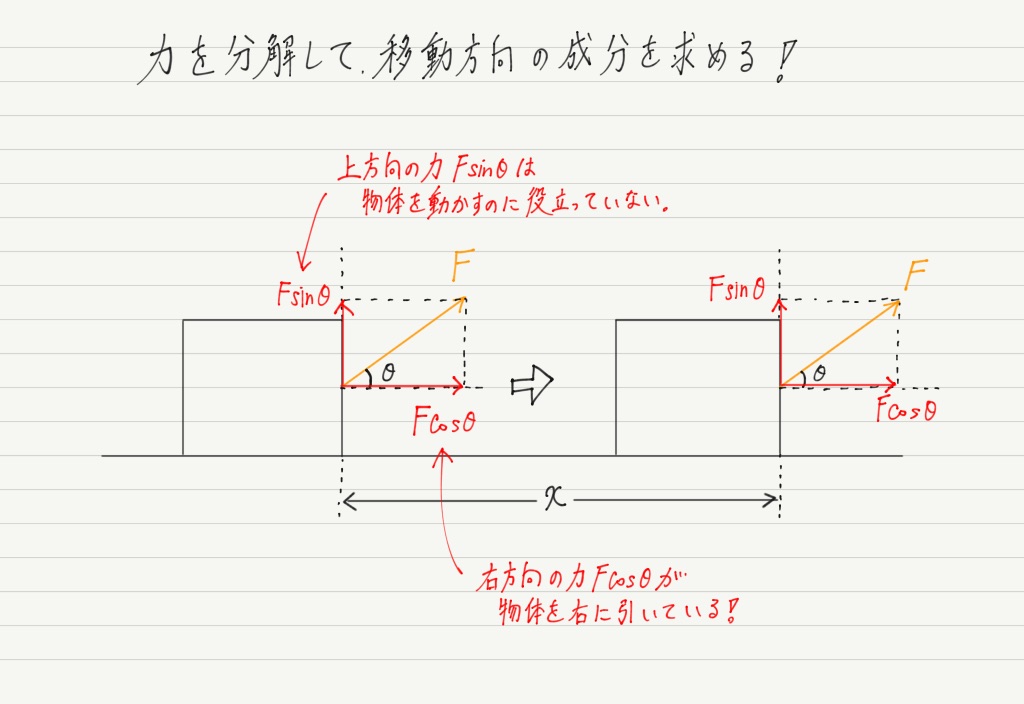
これを用いて，力を分解してみましょう。

このように力を分解すると，「実際に移動方向に物体を動かす力の大きさはFcosθ」ということが分かります。

これによって，仕事Wは，力（Fcosθ）× 距離（x）で，W = Fxcosθと計算できます。

本編では三角比を未習 or 不慣れな人のため，cosθを使わずに3パターンに分けて紹介しましたが，その3つも実は今回の式から導くことができます！
三角比は使いこなせると本当に便利！

今回はこれにて終了。時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！