定積,定圧,等温,断熱と,ここまで様々な気体の状態変化を扱ってきましたが,最後にそれらをまとめておきたいと思います。
理想気体の状態変化と熱力学第1法則
これまでにさんざん言ってきましたが,気体の状態変化を扱う上で軸となるのは熱力学第1法則です。
そこで,今回のまとめも熱力学第1法則を軸にしていきます。
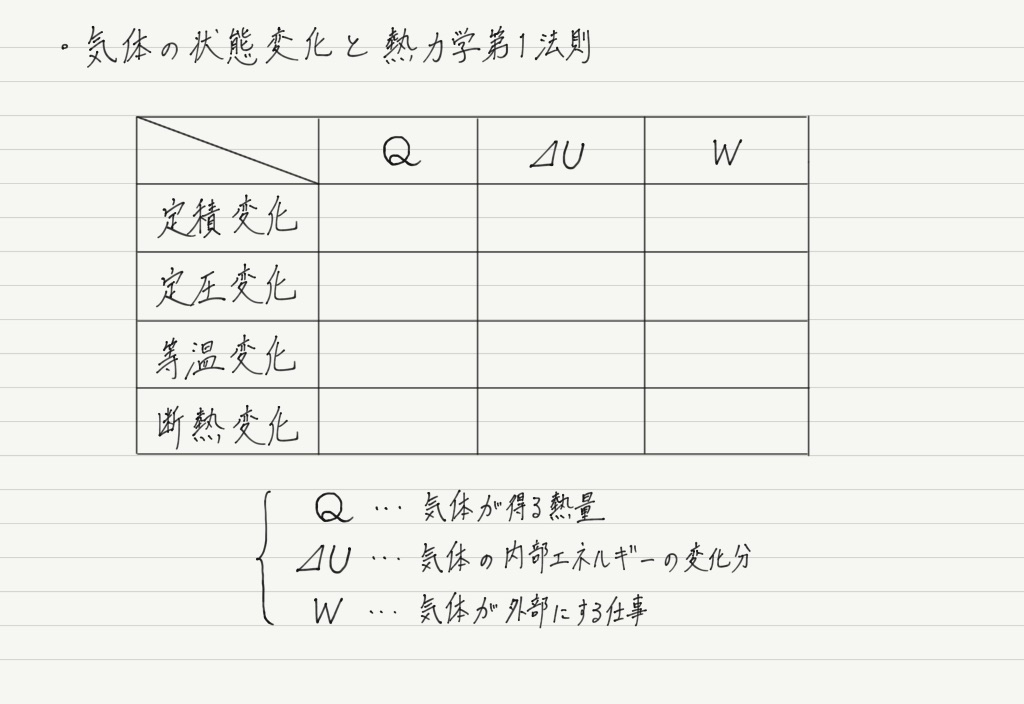
各状態変化について,この表を完成させるのが今回の目標。
ではさっそくわかるところから表を埋めていきましょう!
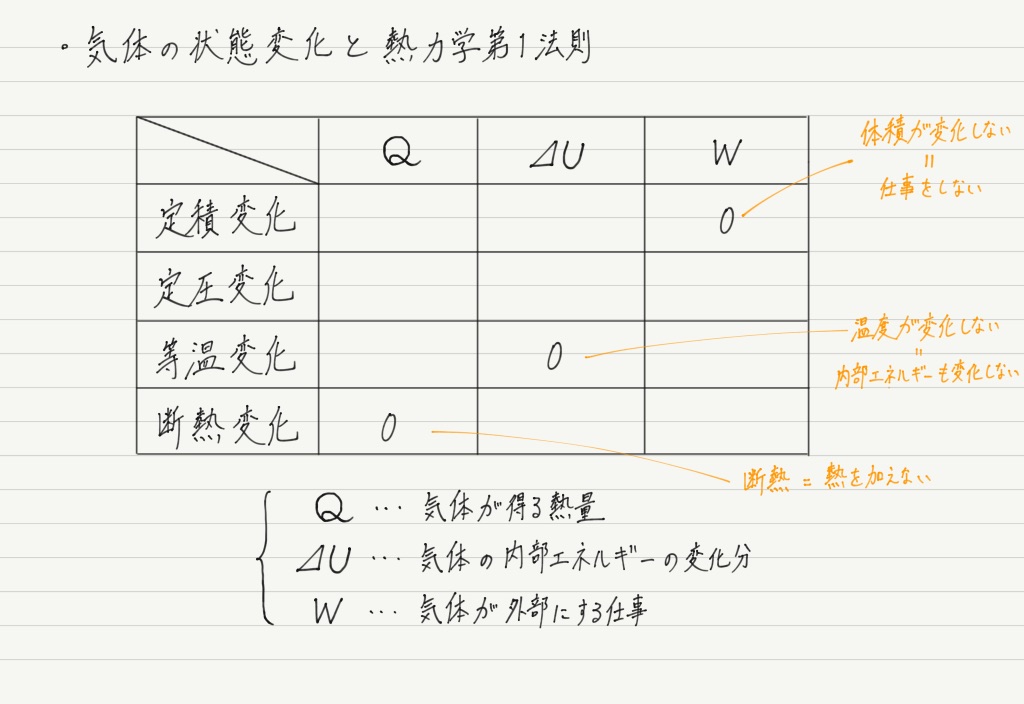
手順① 0が入るところを探す
真っ先に埋められるのは,0が入るところ。
これで手順①はOK。
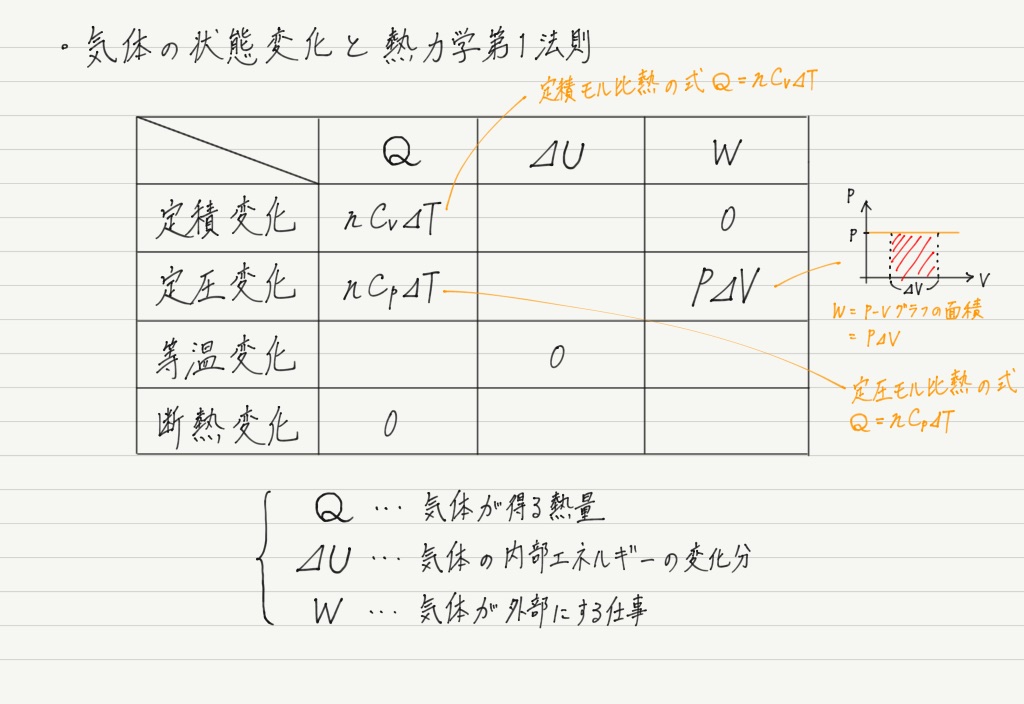
手順② 公式の利用
次に,状態変化の特性が利用できる部分を埋めます。
該当するのは定圧変化での気体のする仕事や,定圧・定積モル比熱。
これらは公式として覚えているはずなので,そのまま表に入れちゃいましょう!
ハイ,手順②終了。
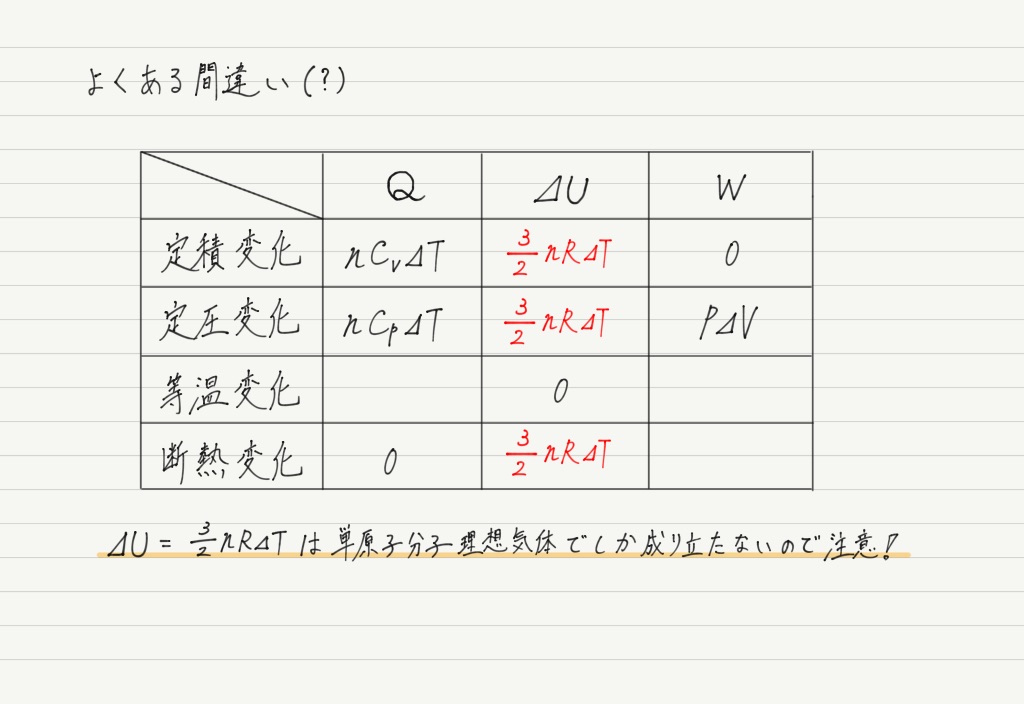
手順③ ⊿Uを求める
次に⊿Uを埋めていくのですが,早とちりして間違えないようにしましょう。
今回は理想気体についてまとめていますが,単原子分子理想気体とは一言も言っていません!
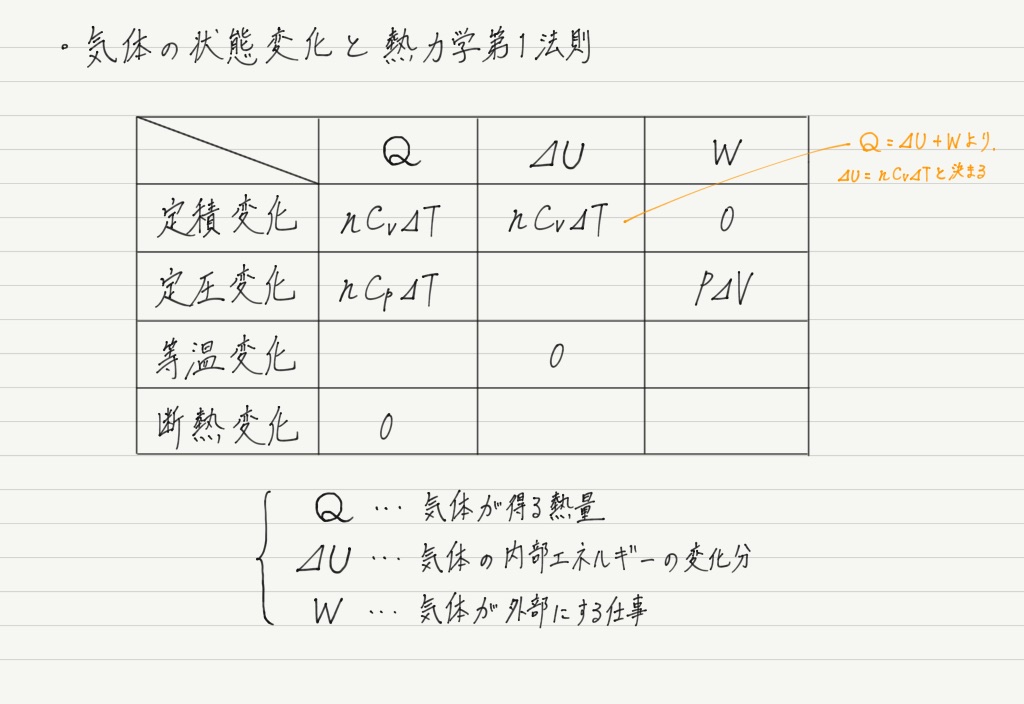
よって別の方法で⊿Uを求めます。 注目すべきは定積変化の行。
QとWがすでに埋まっているので,熱力学第1法則を適用して⊿Uが求められます!
これで内部エネルギーの式が判明しました。
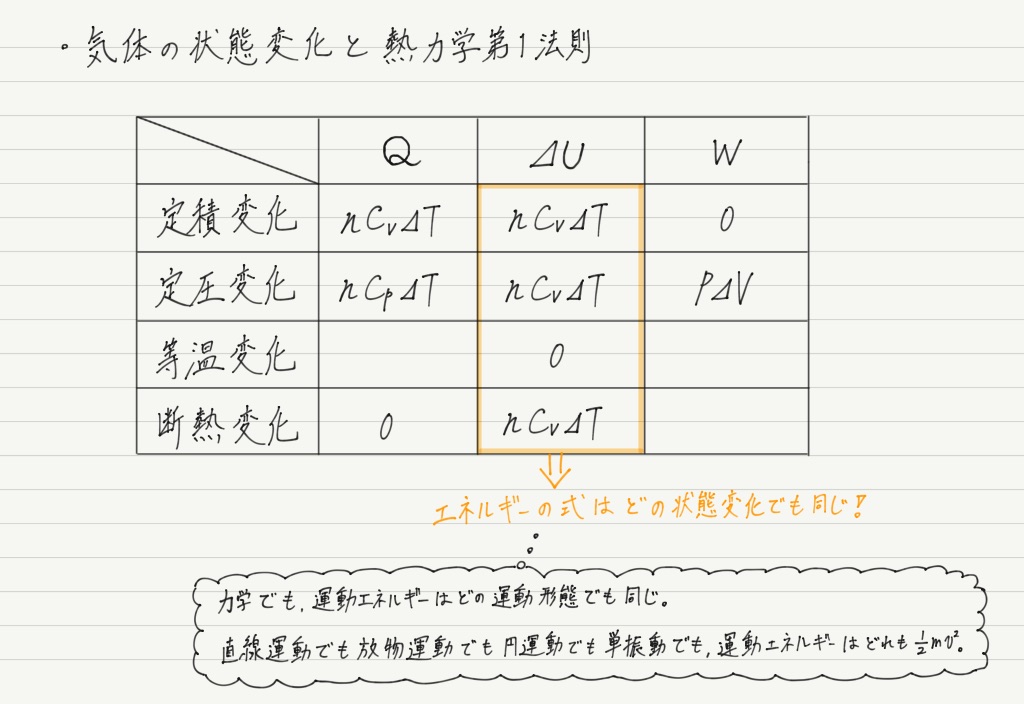
さて,内部エネルギーというのは気体分子の運動エネルギーの総和なので,定積変化だろうが定圧変化だろうが断熱変化だろうが求め方は変わらないはず!
よって,表はここまで埋めることができます ↓
だいぶ埋まってきましたね!
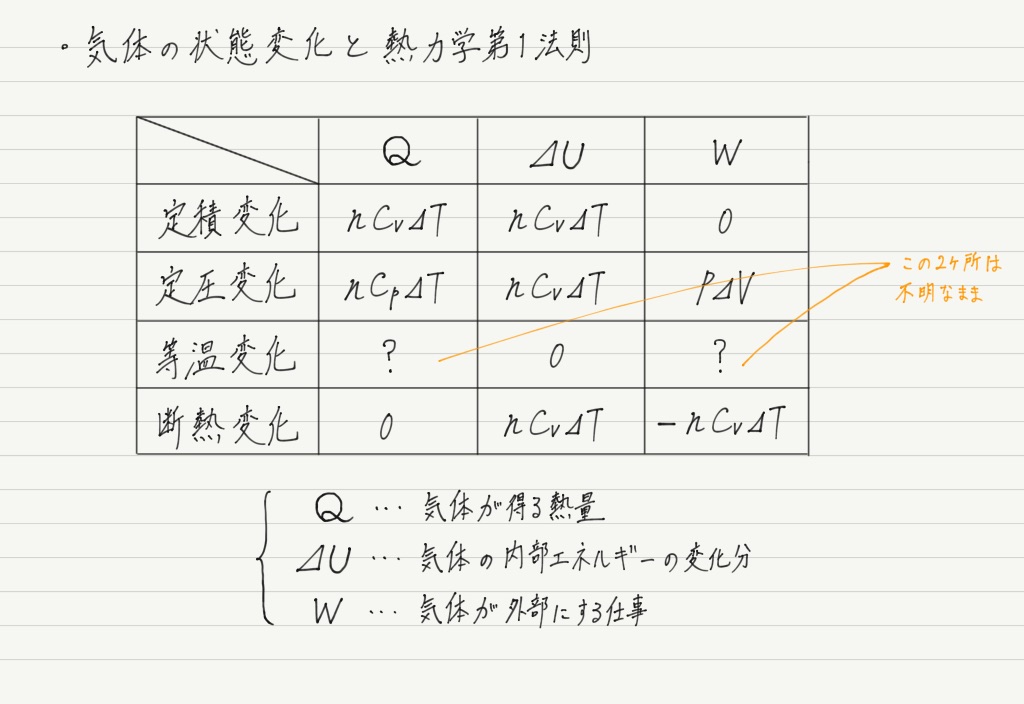
手順④ 第1法則を用いて残りの空欄を埋める
あとはまたQ=⊿U+Wの関係を使うだけ。
最終的に表はこのような姿になります。
この表は丸暗記はしないでください。それは無意味。
丸暗記ではなく,今の手順に沿ってこの表をいつでも作れるようにしておくこと。
それができるようになれば,どんな状態変化の問題が来てもその場で対応できるはず!
マイヤーの関係式
ところで,定圧変化の行は手順③が終わった時点ですべて埋まっていたので,この行にはまだ熱力学第1法則を使っていません。
表は完成したけど,試しに熱力学第1法則を用いてみましょう!
面白いことに定積モル比熱と定圧モル比熱の関係式が出てきました!
これはマイヤーの関係式と呼ばれています。
単原子分子理想気体の定積モル比熱と定圧モル比熱の値は前回すでに求めているので,マイヤーの関係式が本当に成り立っているのか確かめてみましょう。
単原子分子理想気体と二原子分子理想気体ではモル比熱の値が異なりますが,マイヤーの関係式は問題なく成り立ちます。
(二原子分子のモル比熱の値を覚える必要はナシ。)
今回のまとめノート
さっきも書きましたが,このまとめの表は覚えるものではありません。
空白の状態から自力で書けるようにしましょう。
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
今回の記事で熱分野はすべて終了。
ここまで読んでくださり,ありがとうございます。
熱分野を苦手とする人は多いですが,私の書いた記事が少しでも助けになっていれば幸いです。
よく復習し,次のステップへ進んでください!