熱の分野も少しずつ終わりに近づいてきました…!
最終的にはこれまで学んだ状態方程式や,熱力学第1法則,内部エネルギーなどを用いて,気体の変化(温度を上げる,体積を減らす,etc…)についてあれこれ計算できるようになるのが目的なのですが,その前にもう1つだけ気体を調べる手段を伝授します!
P-Vグラフの利用
「気体がした仕事」というのは,問題を解く上でかなり重要な要素です。
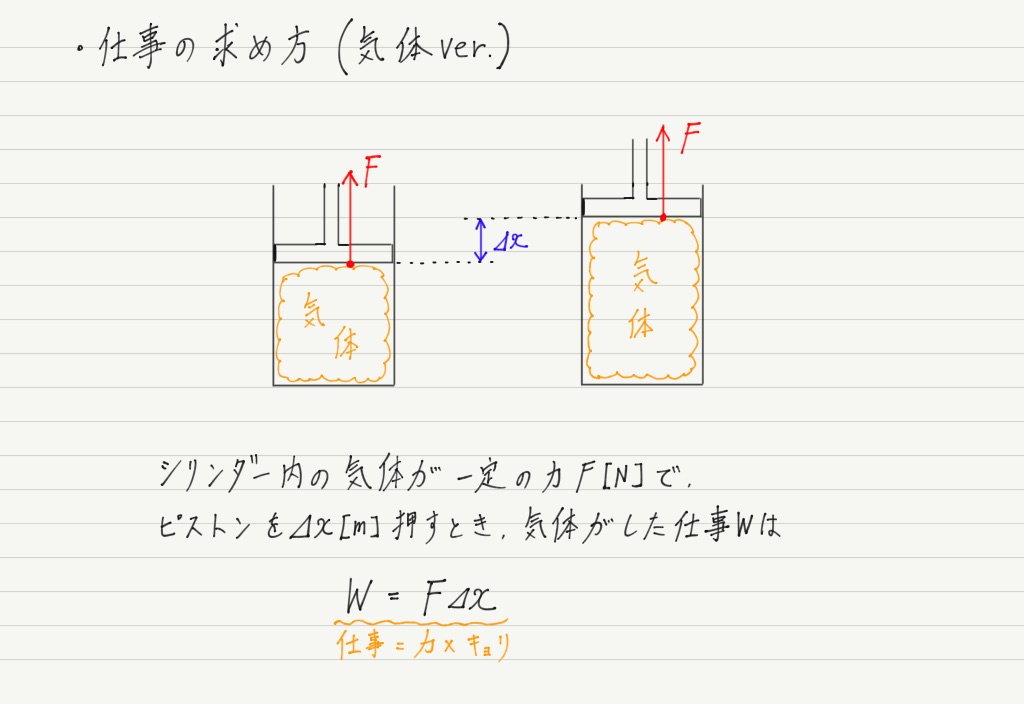
仕事の求め方は力学で習ったとおりなので,実際に計算してみましょう!
これはこれで問題ないのですが,気体の問題では力を使って計算することはほぼありません。
気体では力そのものよりも圧力のほうが使いやすいです!
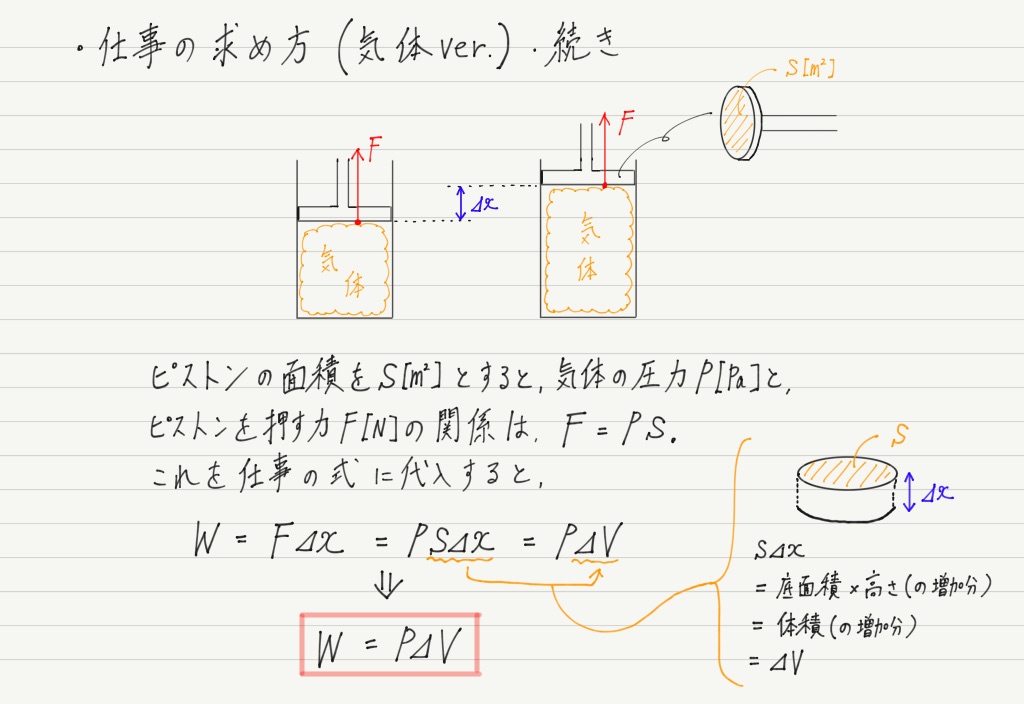
上で計算した仕事の式を圧力を用いて書き換えてみましょう。
これが気体がする仕事を求める式になります!
…しかし,これはあくまでもピストンを押す力(圧力)が一定のとき。
圧力が一定でない場合,当然この W = P⊿Vの式は使えません。
(※ 力学でも,W = Fxは力が一定でないと使えない。)
圧力が変化してしますような状況で,気体のした仕事を求めるにはどうしたらいいでしょう?
物理基礎からここまで学んできた人なら,「計算で求められないのなら,グラフを使おう!」というアイデアが思い浮かぶはず!
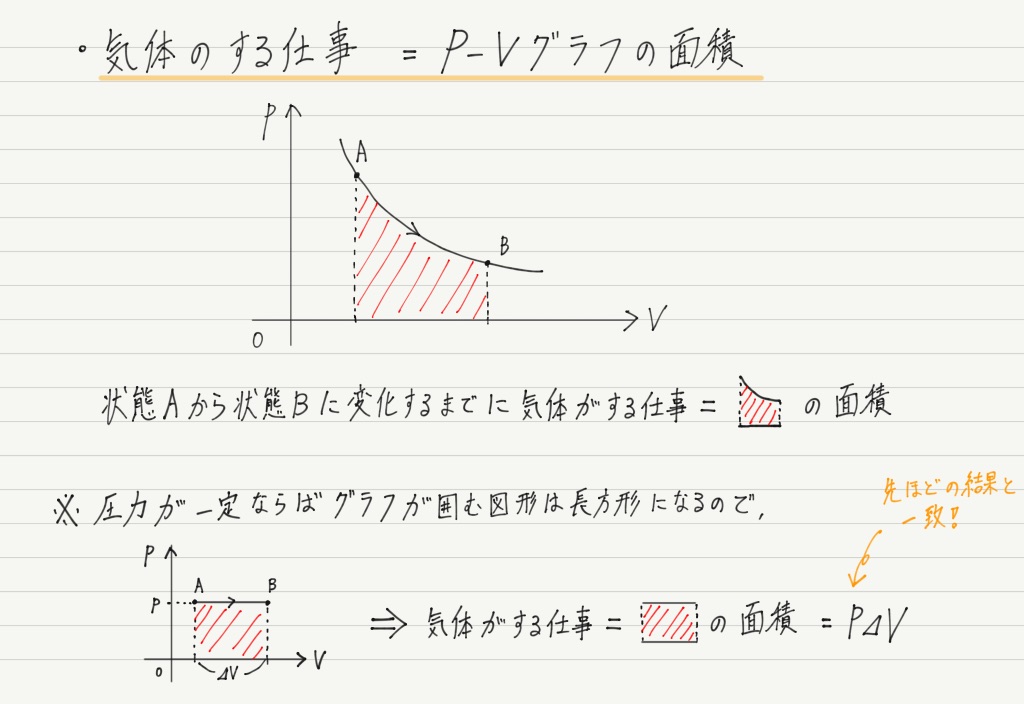
力が一定でない場合の仕事がF-xグラフの面積で求められたのと同様に,気体の仕事はP-Vグラフの面積として求められます!
気体の問題でP-Vグラフが与えられている問題は少なくありません。
値を読み取るだけでなく,面積にも注目するように心がけましょう!
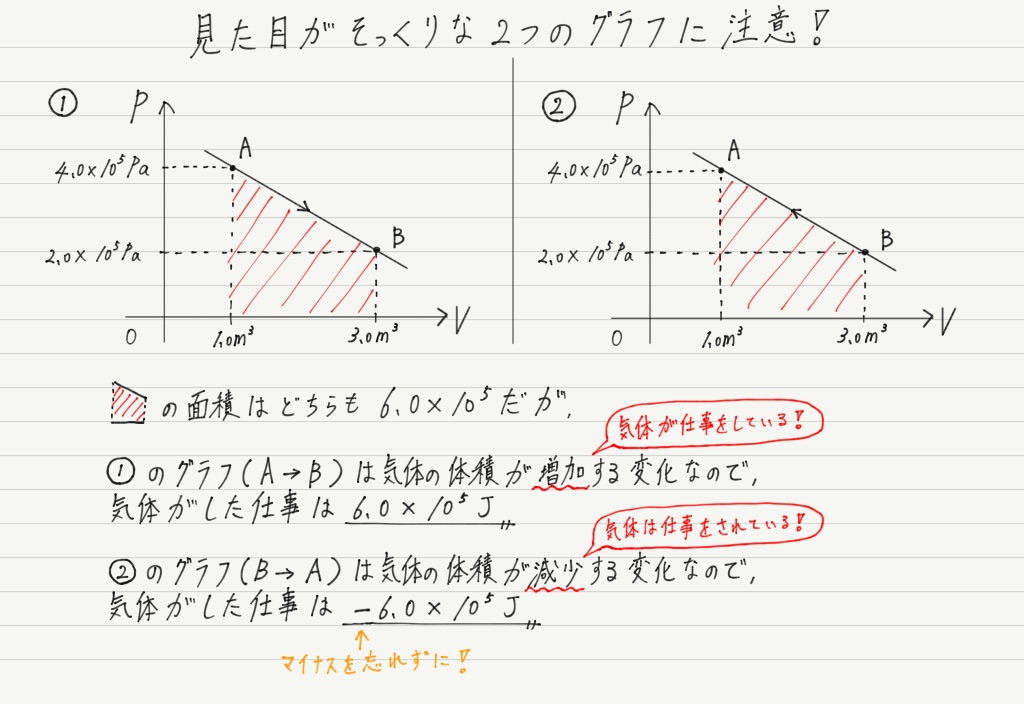
面積の “符号” に注意
力学における仕事もF-xグラフの面積として求められるので,気体の仕事が面積で求められることにさほど驚きはありません。
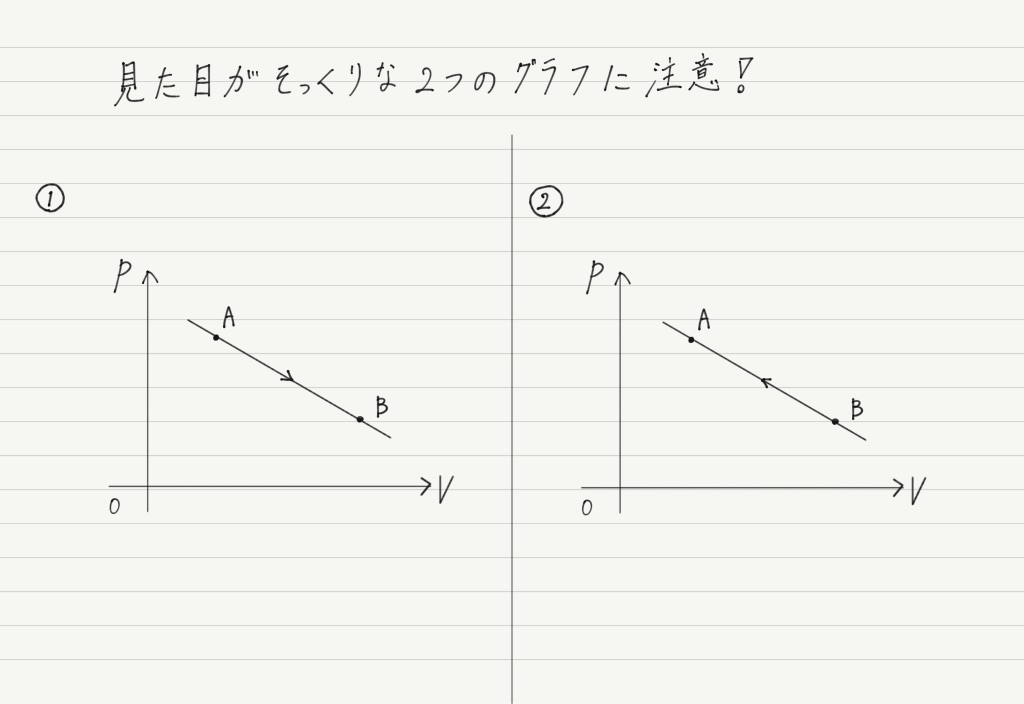
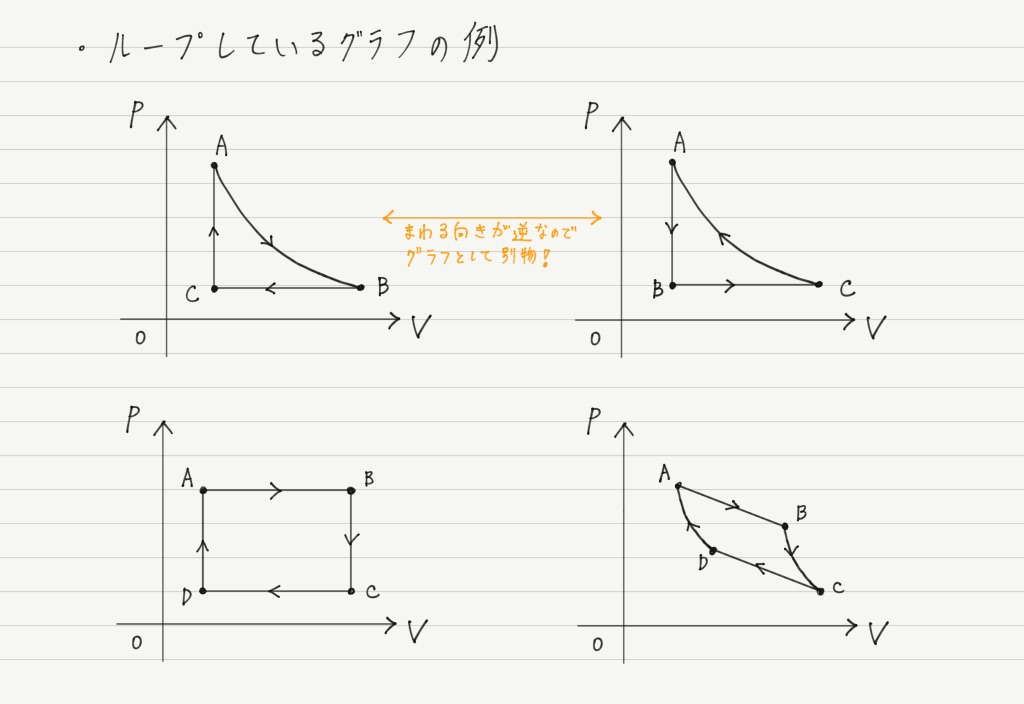
ただし,力学のときにはなかった注意点があります。 この図を見てください。
この2つはグラフとしての見た目は同じですが,普通のグラフとちがって向きがついています。
気体の変化は,「Aという状態からBという状態へ」というように,必ずスタートとゴールが存在します。
よって,グラフを見るときも「どっちからどっちへ向かうのか」を常に意識しなければいけません。
それを表しているのが,グラフについた矢印なのです。
…まぁ,それだけなら見た目だけの話で終わりなのですが,その方向によって気体のする仕事が変わってしまうので要注意です。
見ての通り,気体が仕事を “した” のか,それとも “された” のか,というちがいです!
右側へ向かう矢印 → 体積が増加 → 気体が仕事をした → 仕事は正
左側へ向かう矢印 → 体積が減少 → 気体が仕事をされた → 仕事は負
というわけで,求めた面積に適切な符号をつけてやる必要があります。
仕事を「した」「された」のちがいに自信がない人は過去記事で復習しておいてください。
グラフがループしている場合
P-Vグラフが一番よく登場するのが,「気体をいろいろ変化させて,最終的に元の状態に戻す」という問題。
熱機関の問題がこれに該当します。
気体を変化させてまた元の状態に戻す場合,グラフは次のようにぐるっとループした形になります。
(ループを1周することを1サイクルという。)
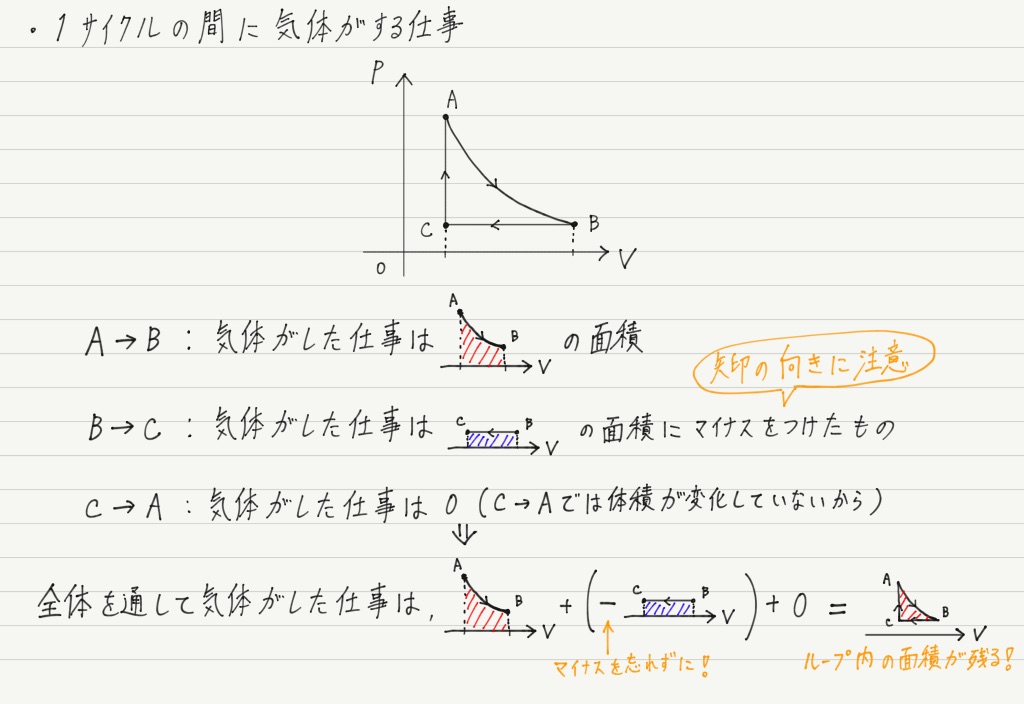
では,この1サイクルの間に気体がする仕事を求めてみましょう!
このようにサイクルで囲まれた部分が,1サイクルの間に気体がする仕事になります!
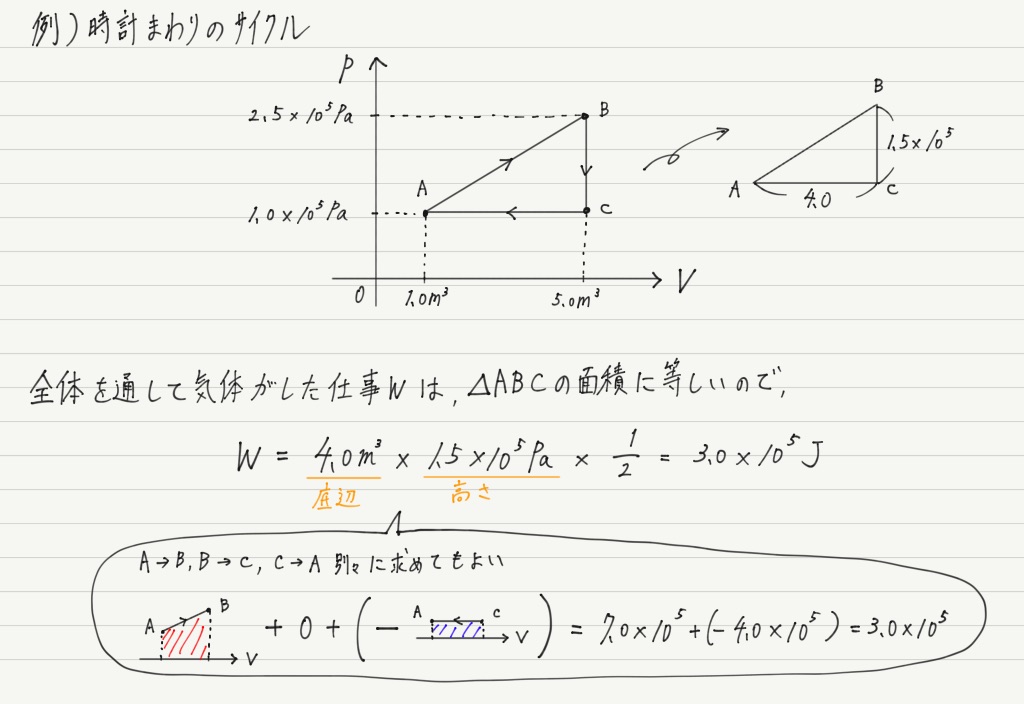
この例ではグラフが曲線なので具体的に面積を求めるのは難しいですが,直線で囲まれている場合は三角形や長方形,台形の面積の公式を使って求められるはずです。
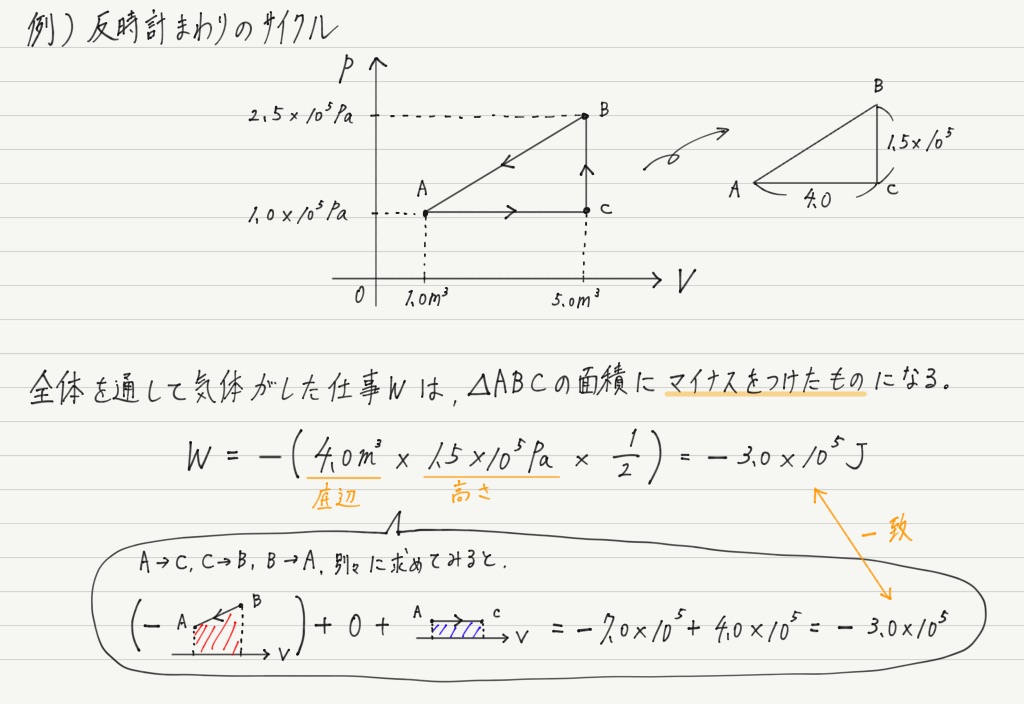
では,ループの向きが反時計回りだとしたらどうなるでしょう?
このように,反時計回りのサイクルでは仕事は負(=気体は仕事をされている)になります!
グラフを使った仕事の求め方はとても便利ですが,くれぐれも符号を間違えないようにしてください。
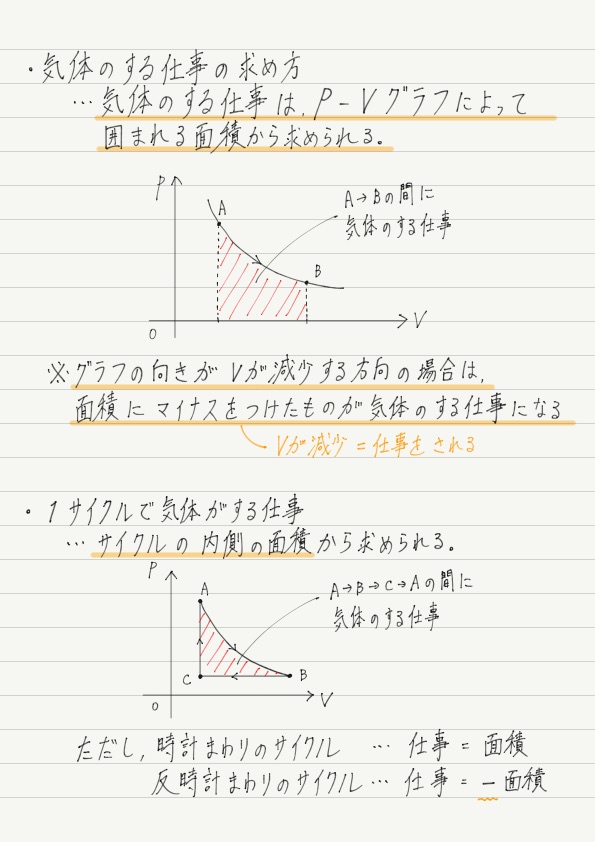
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
気体の問題で定圧変化や定積変化などが次々出てきて,何が何だかわからん!っていう人はいませんか?
次回から数回に分けて,この「◯◯変化」をひとつずつ丁寧に解き明かしていきたいと思います。