物理のヒント『三角比と三角関数』の講義内容に関連する演習問題です。
講義編を未読の方は問題を解く前にご一読ください。
問題
[Level.1]
(ア)〜(オ)のそれぞれの場合について,sinθ,cosθ,tanθの値をそれぞれ答えよ。
値がない場合は「値なし」とすること。
(ア)θ=45°
(イ)θ=60°
(ウ)θ=90°
(エ)θ=\(\pi\)
(オ)θ=\(\frac{7 \pi}{4}\)
[Level.2]
\(\cos \theta=\frac{2}{3}(0\ \text{≦}\ \theta <2 \pi)\)のとき,\(\sin \theta\)の値はいくらか。
[Level.3]
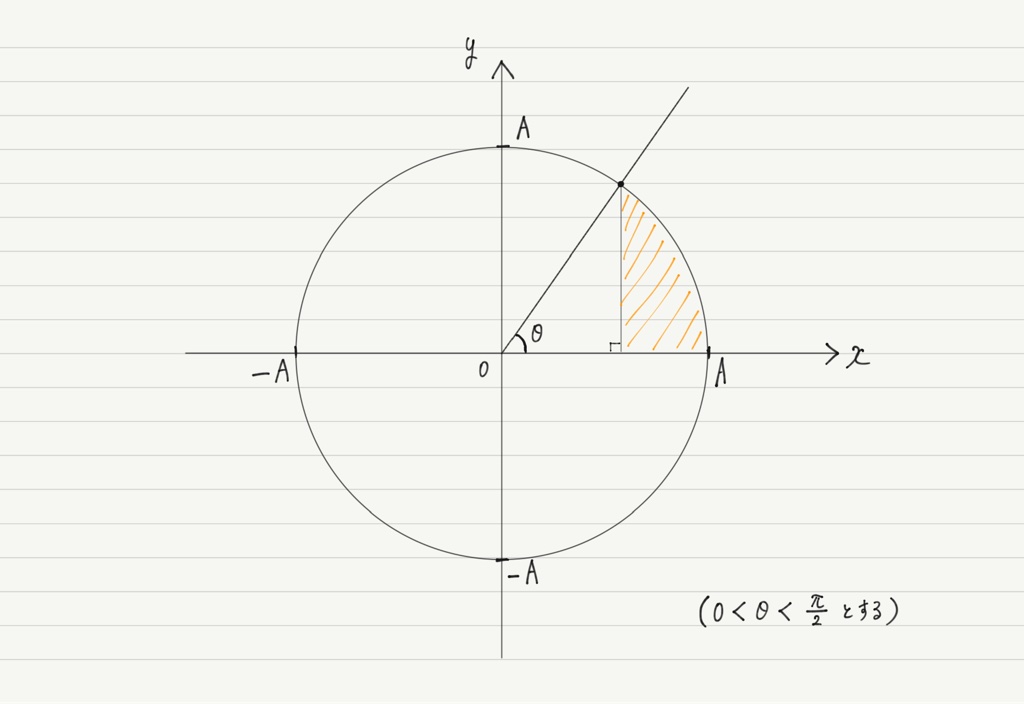
下図の斜線部の面積を求めよ。
この下に答えを載せていますが,まずは自力で考えてみましょう。
答え
[Level.1]
(ア)\(\displaystyle \sin 45° =\frac{1}{\sqrt{2}},\cos 45° =\frac{1}{\sqrt{2}},\tan 45° =1\)
(イ)\(\displaystyle \sin 60° =\frac{\sqrt{3}}{2},\cos 60° =\frac{1}{2},\tan 60° =\sqrt{3}\)
(ウ)\(\displaystyle \sin 90° =1,\cos 90° =0,\tan 90°\)は値なし
(エ)\(\displaystyle \sin \pi =0,\cos \pi =-1,\tan \pi =0\)
(オ)\(\displaystyle \sin \frac{7 \pi}{4} =-\frac{1}{\sqrt{2}},\cos \frac{7 \pi}{4} =\frac{1}{\sqrt{2}},\tan \frac{7 \pi}{4} =-1\)
[Level.2]
\(\displaystyle \sin \theta=\pm \frac{\sqrt{5}}{3}\)
[Level.3]
\(\displaystyle \frac{1}{2}A^{2}(\theta -\sin \theta \cos \theta)\)