いよいよ力学も大詰めを迎えました。 高校力学最後の話題は天体の運動。
これまでに習った力学の知識が,糸で引かれる台車の運動や斜面上の小球の運動にとどまらず,天体の運動にも適用できることを体感してほしいと思います!
物理のスケールのでかさよ!!
ケプラーの法則
古来より人々は星の運動に注目してきました。
星座にまつわる神話や,天動説 VS 地動説など,星に関する話題には事欠きませんが話が長くなるといけないので,コペルニクスが地動説を唱えた後の16世紀後半から話を始めましょう。
まだ望遠鏡が発明されていないこの時代に,肉眼で(!)極めて精密な天体観測を行ったのがデンマークの天文学者ティコ・ブラーエです。
そしてブラーエの死後,助手だったケプラーはブラーエの遺した精密なデータを整理し,そこから惑星の運動に関するいくつかの結論を得ました!
その結論をまとめたものが,今日ケプラーの法則として知られているものです。
第1〜第3法則までありますが,まずはすべて紹介しましょう。
ケプラーの法則に関してまず1つ注意しておきます。
上の記述を見ると,ケプラーの法則は太陽とその惑星についての法則に見えますが,それはブラーエは太陽系の惑星を観測し,ケプラーはそのデータを基にこの法則を見つけたことによるものです。
実際にはケプラーの法則は太陽とその惑星に限らず,中心となる天体とその周りをまわる天体に関して常に成り立つことが知られています(例えば「地球と月」,あるいは「地球と人工衛星」でも成り立つ)。
参考書や問題集に載っている問題は地球を中心天体としている場合が多いですが,安心してケプラーの法則を使ってください。
ケプラーの第1法則について
天動説にしろ地動説にしろ,当時の人間は天体の運動は円運動であると考えていました。
円は形が対称的で美しい図形なので,「神様がこの宇宙を創ったのなら,星の運動は円を描くにちがいない」と信じていたのです。
が,これに堂々と異を唱えたのがケプラーの第1法則!!
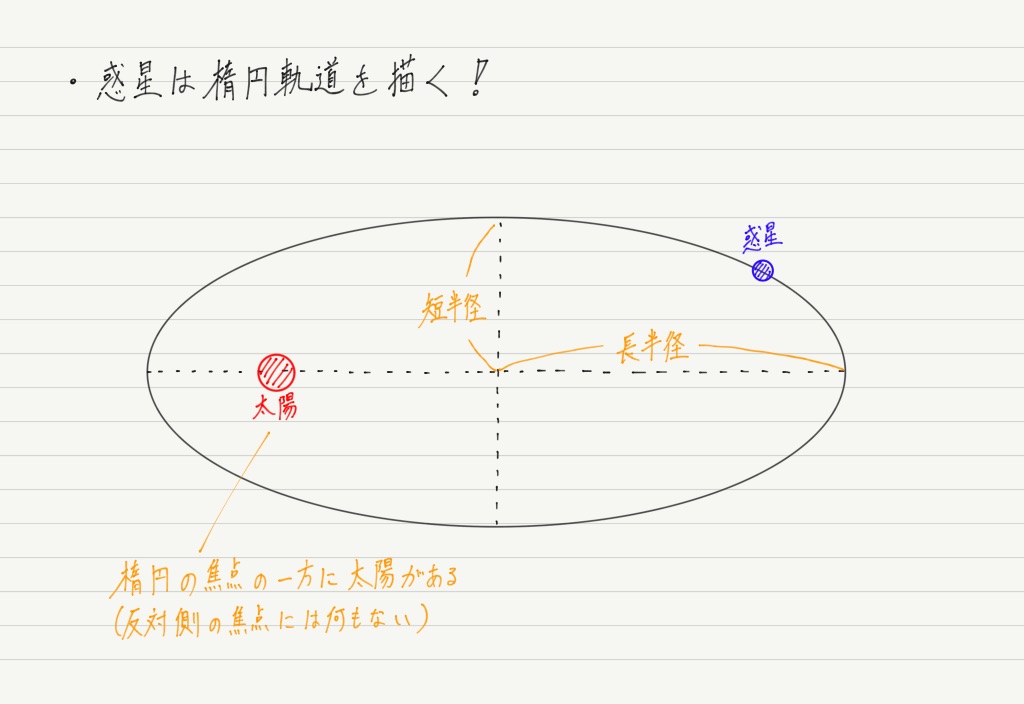
ケプラー(というかブラーエのデータ)によれば,惑星は完全な円ではなく楕円を描いており,しかも太陽は楕円の中心ではなく,焦点にあるというのです。
(楕円の焦点って何?っていう人は,数学の2次曲線の分野を参照してください。)
ちなみに太陽系の惑星が描く楕円はこの図のような平べったい楕円ではなく,ほぼ円です。
楕円がどれだけ円に近いかは楕円の長半径と短半径の比を見れば分かりますが,もっとも比が大きい水星でさえ1:0.97です。
その他の惑星はこれよりさらに1:1に近い。
…ブラーエが肉眼でこのわずかなちがいを見抜いていたってやばくない?
そしてその測定データを見て,「これは誤差ではなく楕円を描いている証拠だ」と結論づけたケプラーもやばくないか?
ケプラーの第2法則について
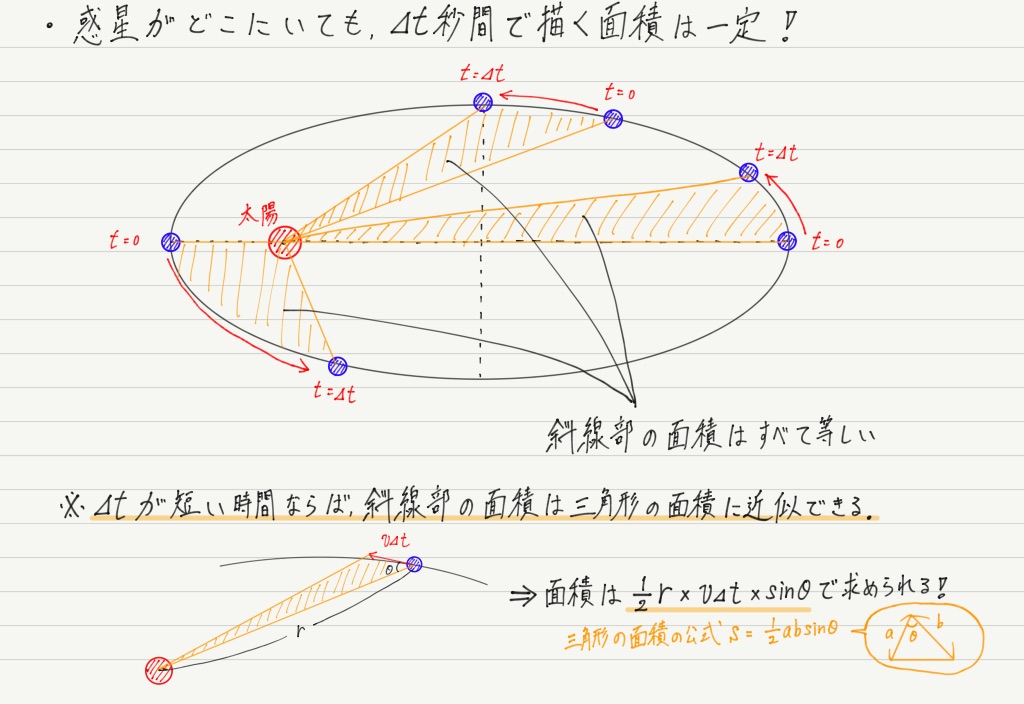
第2法則は文章で書くよりも,図を見た方が理解しやすいと思います。
(補足:この面積をかかった時間⊿tで割ったものは面積速度と呼ばれ,実際に計算をする場合は面積速度を用いる。)
第2法則は要するに,惑星が公転する速さは一定ではなく,中心天体との距離が近いときには速く,遠いときにはゆっくり進むということを言っています。
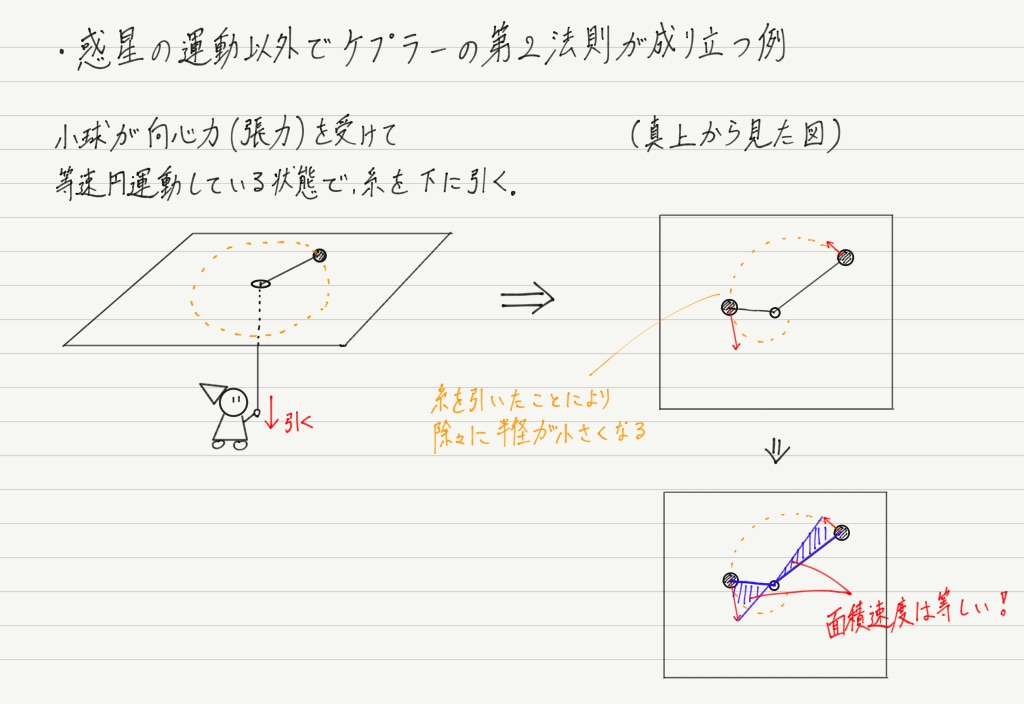
なお,この第2法則は惑星の運動に限って成り立つわけではなく,物体がある1点に向かって力を受け続ける運動ならば,必ず成り立つことが知られています!
ケプラーの第3法則について
第3法則については,ある値の2乗と別の値の3乗が比例するなんてよく見つけたな…っていうのが率直な感想。
それ以外の感想は特にない(笑)。
この第3法則は問題を解くときにどうやって使うのかわからない人が結構多いみたいなので,伝授したいと思います。
ポイントは,「中心天体が同一ならば,比例定数は常に一定の値をとる」こと。
問題を解く際は,この “一定” を利用します。
熱分野の「ボイル・シャルルの法則」と同じような使い方をする,と思っておけばよいでしょう。
例題
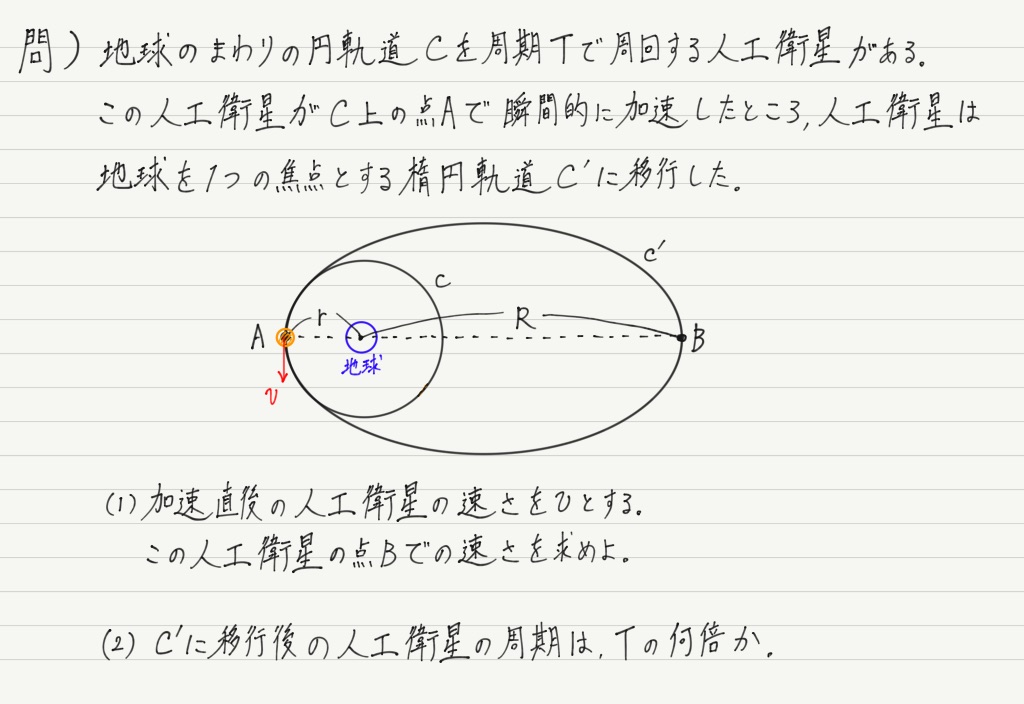
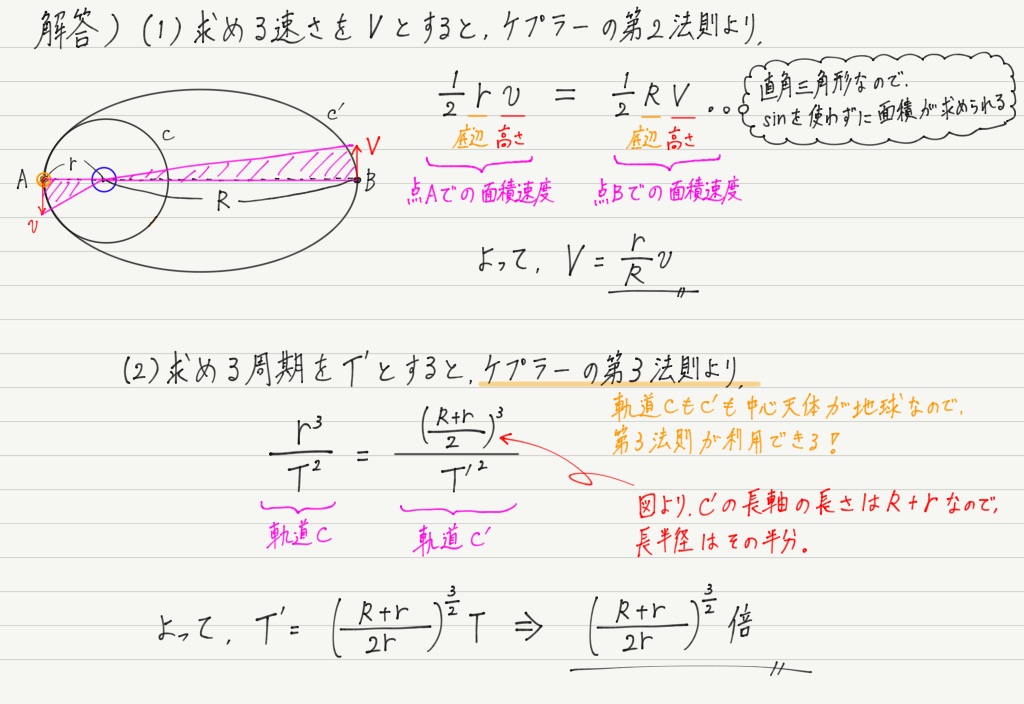
最後に例題をやって確認。
解答は下にあります。 解き終えたらスクロールしてください。
解けましたか? では解答です ↓
入試でケプラーの法則が出題される頻度は高くないですが,ちゃんと勉強した人とそうでない人の差がつきやすい分野です。
決して難しくはないので,しっかり理解しておきましょう!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は天体の運動を語る上で絶対に外せない,万有引力について学んでいきます