【演習】円運動の運動方程式

物理【力学】第14講『円運動の運動方程式』の講義内容に関連する演習問題です。 講義編を未読の方は問題を解く前にご一読ください。

円運動の運動方程式すべての運動は運動方程式によって記述されます。当然円運動も例外ではありません！円運動の運動方程式とはどのようなものでしょうか？...

問題

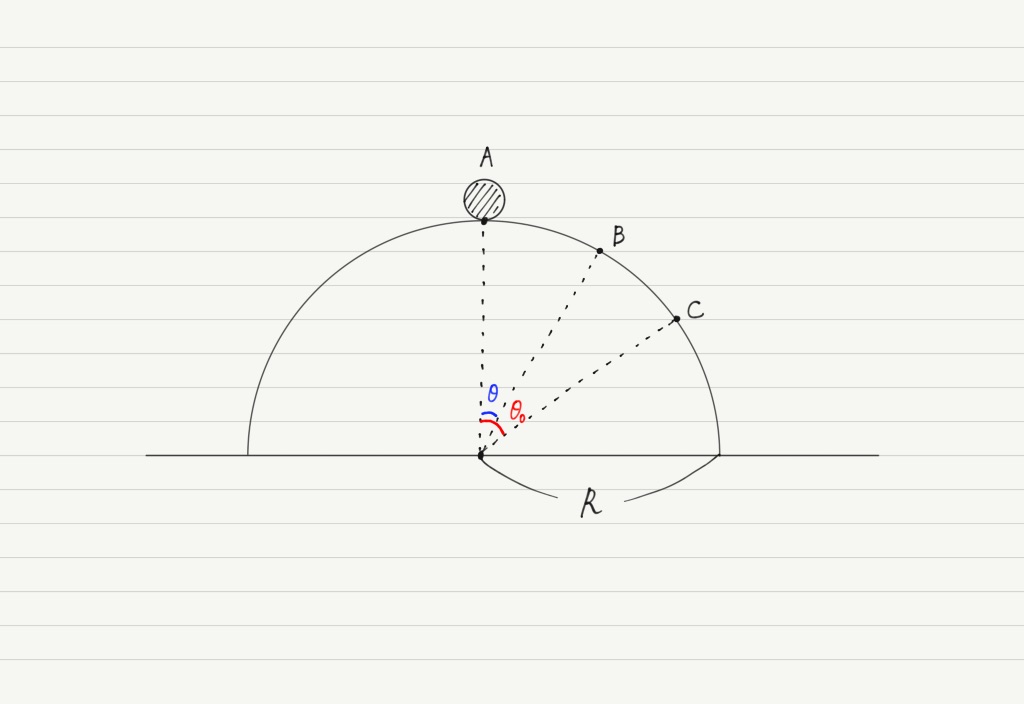
下図のようななめらかな円筒面上の頂点Aに質量mの小球を置き，静かに手を離した。 小球ははじめ円筒面上を時計まわりに運動するが，やがて円筒面を離れる。 円筒の半径をR，重力加速度をgとして以下の各問に答えよ。

[Level.1]
小球は面から離れることなく，図中の点Bを通過した。 点Bにおける小球の速さを求めよ。

[Level.2]
点Bにおいて，小球が面から受ける垂直抗力の大きさを求めよ。

[Level.3]
小球は図中の点Cで面から離れた。 cosθ₀を求めよ。

この下に答えを載せていますが，まずは自力で考えてみましょう。

答え

[Level.1]
\(\sqrt{2gR(1-\cos \theta)}\)

[Level.2]
\(mg(3 \cos \theta -2)\)

[Level.3]
\(\cos {\theta}_{0}=\frac{2}{3}\)