運動エネルギーと運動量はともに質量と速度から計算できますが,運動エネルギーと運動量ではそれぞれ役割がちがいます。
物体はエネルギーを使って仕事をすることができますが,運動量を使ったら何ができるのでしょう?
今回はそのあたりに焦点を当てたいと思います。
力積とは
運動量を使ったら何ができるか,という問いに対して,我々はもう答えをもっています。
前回の記事で見たように,ボーリングの球は,その運動量(=勢い)を利用してピンを弾き飛ばすことができます。
問題は,これを物理としてどう表現するか,ですよね。。。
ピンが球から受けた影響が仕事として表されないことも,前回学んだとおりです。
なぜ仕事として表せないかというと,力が一瞬しかはたらいていないことが原因でした。
そこで,衝突時の力のような,一瞬しか作用しない力(「撃力」という)が及ぼす作用を新しく考えましょう!
「一瞬」とはいえど,ハイスピードカメラ等で撮影すれば,球とピンが接触している時間は測定できるはずです。
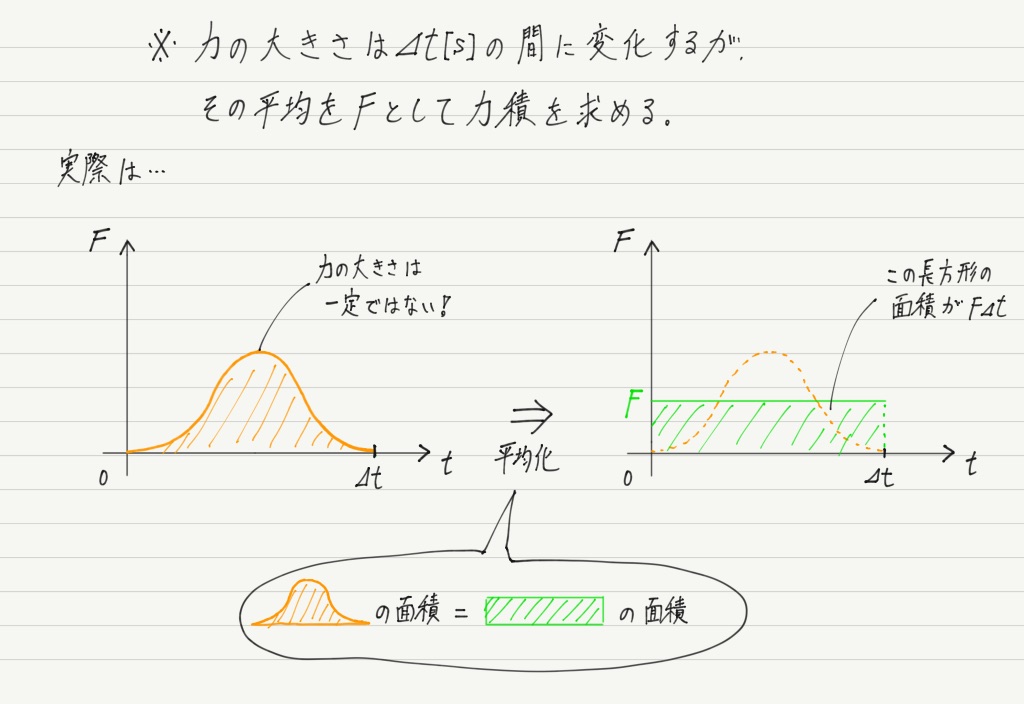
このごくわずかな接触時間を⊿ t[s],その間に球がピンに与える力をF[N]として,これらの積,F⊿ tを「力積(りきせき)」と名付けます(単位はN・s)。
この力積が,撃力が及ぼす作用を表す量となるのです!
仕事が「力 × 距離」という式なのに対し,力積は「力 × 時間」という式なので,なんとなく対になっている感じがしませんか?
力積と運動量との関係
いくら仕事と対になっているように見えるからとはいえ,突然出てきた「力 × 時間」という値に意味はあるのでしょうか?
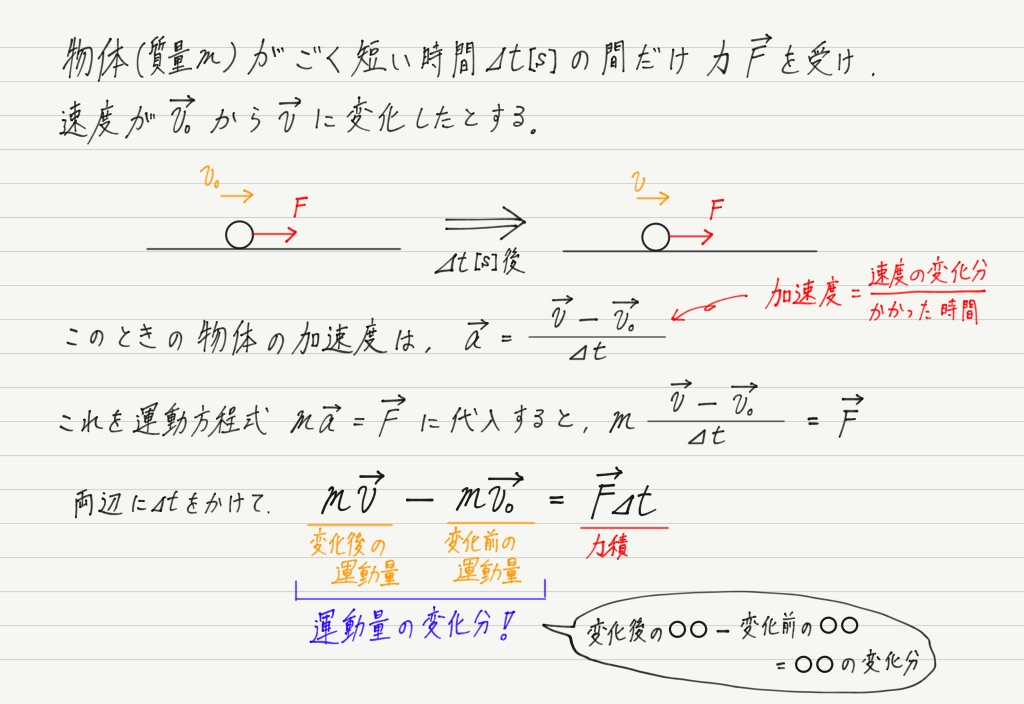
実は,運動方程式をすこーし式変形すると,力積が自然に式の中に登場します。
そればかりか,とても興味深い事実を教えてくれます。
なんと!「 運動量の変化分=力積」という関係が飛び出しました!
運動方程式ってやっぱりすごい!!
ところでこれ,物理基礎でやった「エネルギーの変化分=仕事」という関係にとても似ていませんか?
この関係式を見れば,「仕事と力積が対になっている」というのが見た目だけの話ではなく,物理的な意味でも対になっていることが実感できるかと思います。
また,この関係を用いることで,衝突の際に物体どうしにはたらく力の大きさが計算できます。
Fの式を見ると⊿ tが分母にあるので,接触時間がより長いほうが受ける力が小さくなります。
野球をやる人はこれを自然に応用しているはず。
速いボールをキャッチするとき,グローブを引きながらキャッチすると手に伝わる衝撃が少なくなりますよね?
これは引きながらキャッチすることで,ボールとグローブの接触時間を延ばしているためです。
力の “距離的効果”と“時間的効果”
運動エネルギーと運動量は対のようになってはいますが,まったくの別物。
運動エネルギーはスカラー量で,運動量はベクトル量。
運動エネルギーは仕事と関係していて,運動量は力積と関係している。
そもそも求める公式もちがう。
ちがうものだということは分かっていても,いまいち区別がつきにくいなぁと感じる人は多いです。
それはおそらく「大きい運動エネルギーをもつ物体」と「大きい運動量をもつ物体」のイメージが完全にかぶってしまうのが原因でしょう。
「運動エネルギーは大きいけれど運動量は小さい」というような運動の例があればいいのですが,残念ながら「運動エネルギーが大きい物体は運動量も大きく,運動量が大きい物体は運動エネルギーも大きい」です。
まぁ,どちらも質量と速度で決まる量なので仕方ありません。
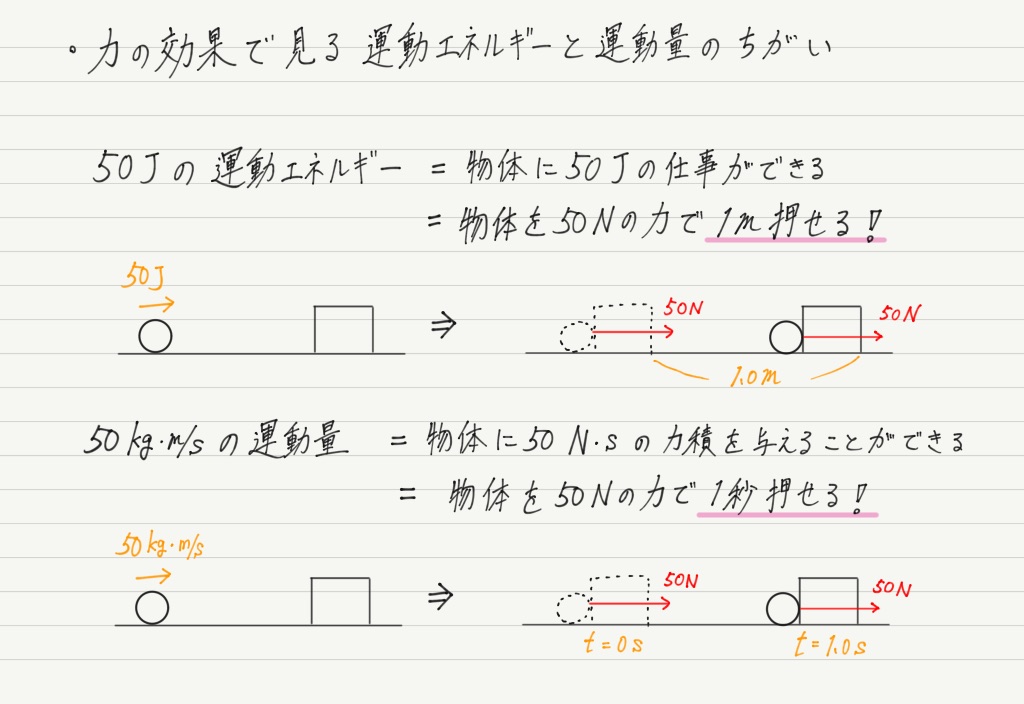
ここでは運動エネルギーと運動量のちがいを,物体そのものではなく,「物体が及ぼす力の効果」に注目して明確にしておきましょう。
(※ 上の図では話をわかりやすくするために1秒という時間を用いたが,力積の⊿tは本来は1秒にも満たないごく短い時間。)
物体を1m押すのと,1秒押すのとでは,話が全くちがいますよね!
この話は運動エネルギーと運動量のちがいを説明するひとつの例として覚えておいてください。
例題
最後に例題をやっておきましょう。
まずは自力で考えてみましょう。
運動量はベクトル量だったので,それと関係する力積もまたベクトル量になることに注意。
では,解答です。
(1)のような直線運動ならば,正負に注意して計算すればOKですが,(2)のような平面運動の場合は,ただ数値を足したり引いたりしてもダメですよ!
ちゃんとベクトルとして計算することが大事です。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
運動量の一番のメリットは物理基礎では扱えなかった「衝突運動」を扱える点です。
衝突運動を調べる上で必須となる法則について紹介していきます。