これまで物体の運動をいろいろと見てきましたが,「物体の大きさ」には言及してきませんでした。
「ばねにつながれた小球が〜」という問題はあっても,「ばねにつながれた半径1cmの小球が〜」という問題はここまでひとつもありませんでしたよね?
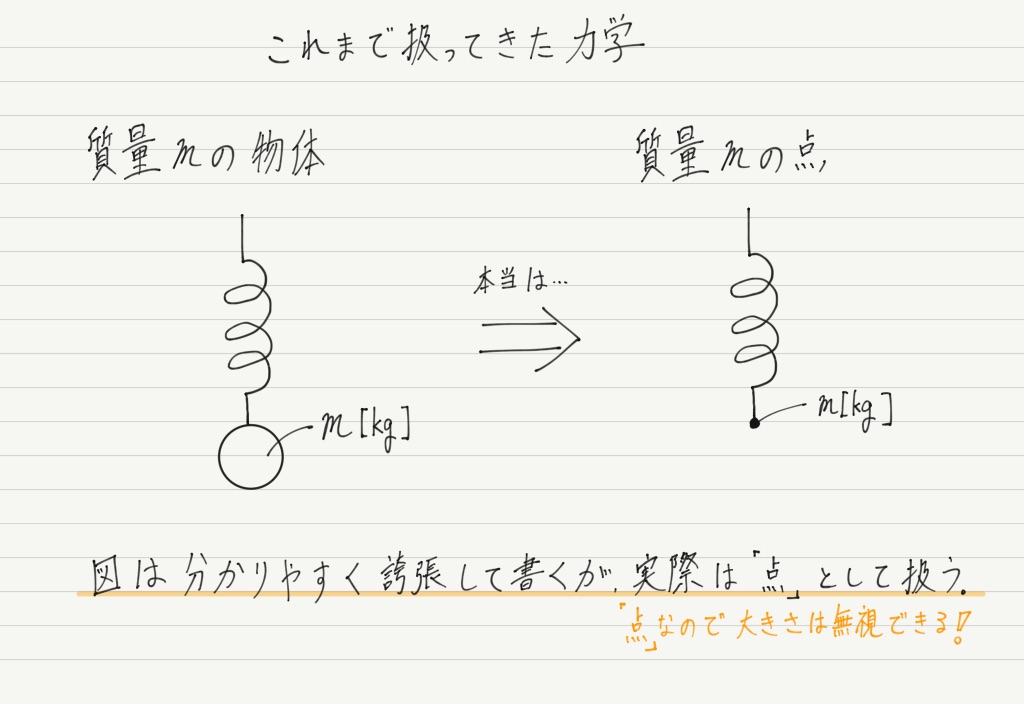
これまで扱っていたのは実は「点」
それもそのはず。 運動方程式や等加速度運動の公式,エネルギー保存則は,物体の大きさに関係なく成り立ちます。
そう,物体の大きさも空気抵抗や摩擦と同様,本質に影響を与えないのです。
本質に無関係なら,物体の大きさは思い切って無視しちゃって「点」とみなしましょう!
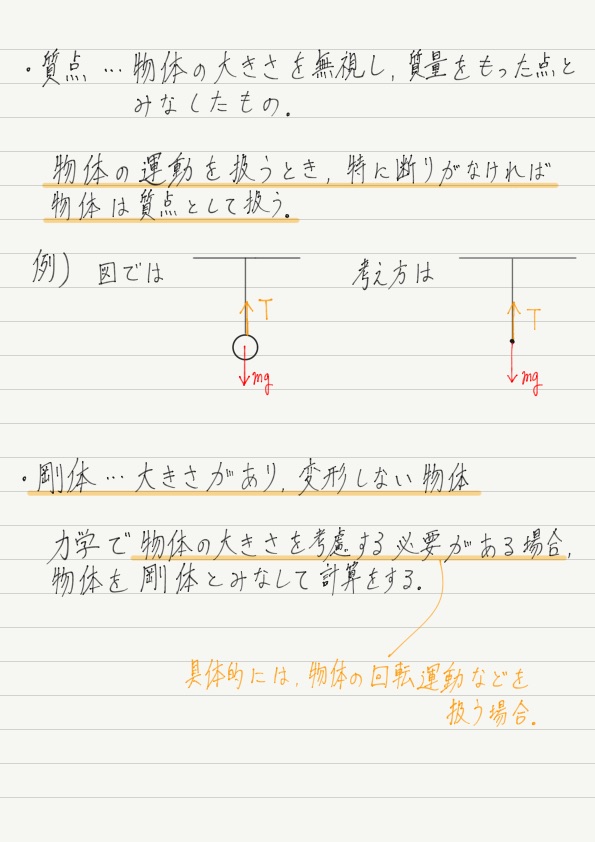
このように質量をもつ点のことを「質点」といいます。
つまり,これまでの力学で勉強してきたのは,物体の運動というより,「質点の運動」なのです。
問題文に「物体」「小球」と書いてあって,図もあたかも大きさがあるように書いてきましたが,実際には物体の大きさを暗黙のうちに無視していました。
これまで質点の話を一切出さなかったのはもちろんわざとです。
物理基礎の一番最初から「大きさを無視できる物体を質点といいます」といわれても??ってなりますからね〜
大きさは本当に不要か
質点という考え方は物事をとてもシンプルにしてくれるので重宝しますが,それだけでは解決できないこともあります。
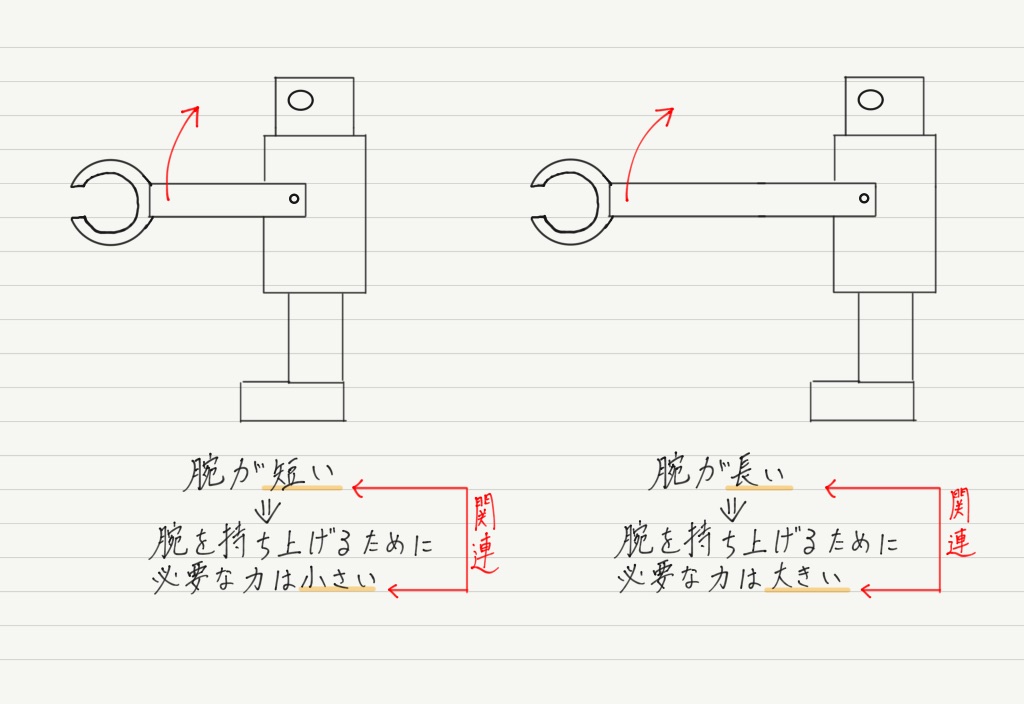
たとえばロボットを作ろうと思ったとき,ロボットの腕を持ち上げるのにどれぐらいの力が必要か計算しなくてはいけませんが,それは腕の長さによって変わってきます。
このように物体の大きさと力の作用が関連している場合,質点という考え方は役に立たず,今度こそ物体の大きさと向き合わないといけません。
前置きがめちゃくちゃ長かったですが,ここで今回のタイトルにある「剛体」について説明しましょう。
剛体とは,大きさをもち,力を加えても変形しない物体のことです。
ただし,物体の変形は複雑なので高校物理では扱いません(例外:ばね)。
よって剛体で大事なのは,「大きさをもつ」物体であるというところ!
大きさが無視できない場合には,質点ではなく剛体を扱うことになります。
ただ,これだけ聞くと勘違いしてしまう人が出てきそうなので補足。
ここでいう「大きさが無視できない」というのは,「非常に大きい」という意味ではありません!!
たとえば,地球は我々から見たら非常に大きい球体ですが,太陽のまわりの地球の公転運動は地球を質点とみなして正しく計算することができます。
大きい物体だけど,大きさを無視してよいという大事な例です。
では「大きさが無視できない」とはどういう意味なのか。
それは,「大きさを考えないと意味がない」ということです。
これには先ほどのロボットの腕や,シーソーの運動,地球の自転などが該当します。
ロボットの腕やシーソーは点で置き換えることができません。
地球は公転を扱う場合は点で置き換えられますが,自転を扱う場合は点で置き換えられない。
さて,この3つに共通するものはなんでしょう?
答えは「回転」です。 ロボットの腕は肩関節を中心に,シーソーは支点を中心に,地球は自転軸を中心に回転します。
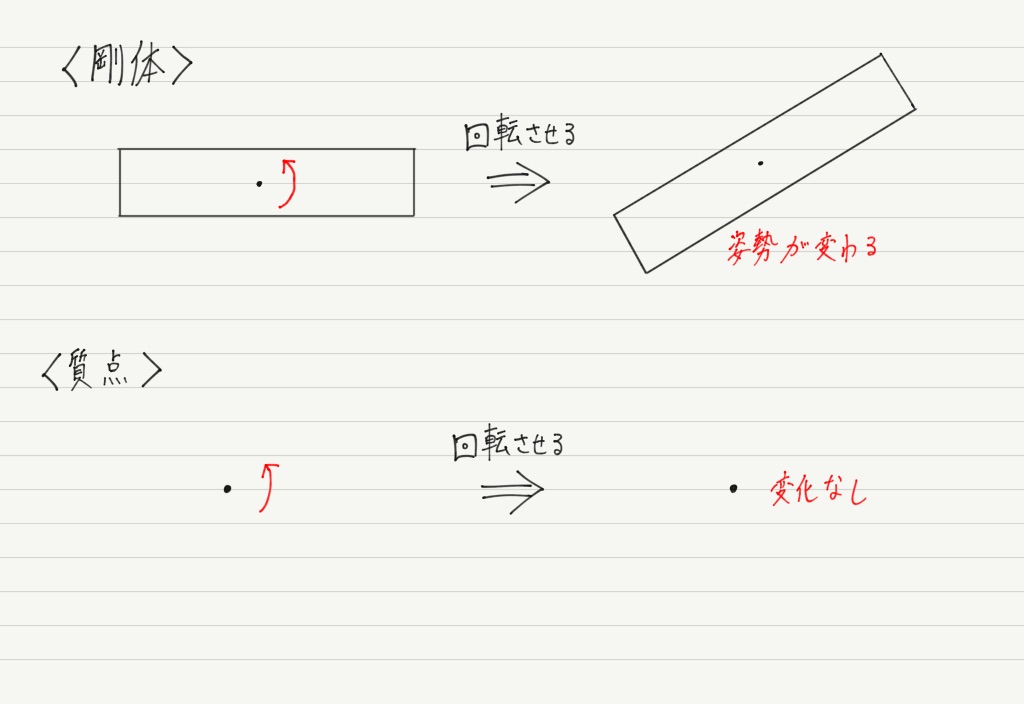
大きさがある物体は回転によって姿勢を変化させますが,点は回転させても点のままです。
このように,質点にしてしまうと回転の様子が分からなくなってしまいます。
「大きさを考えないと意味がない」とはまさにこのこと。
回転,それが剛体の力学の大きなテーマになります。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
「回転」というキーワードが出てきました。 力が剛体を回転させるはたらきについて次回学習しましょう!